Конфигурация магнитных цепей магнитоэлектрических, так же как и электромагнитных устройств разнообразна и зависит от их назначения. Существуют два основных типа магнитных систем: разветвленные и неразветвленные (последовательные). В неразветвленных магнитных цепях основной магнитный поток проходит последовательно через все участки. В разветвленной цепи основной магнитный поток разделяется на несколько отдельных параллельных потоков. Магнитные цепи магнитоэлектрических устройств могут при этом формироваться с использованием постоянных магнитов, намагниченных как в аксиальном, так и в радиальном направлении.
Применительно к магнитоэлектрическому приводу (МЭП), предназначенному для проведения испытаний вязкоупругих свойств эластомеров, для оптимизации его магнитной системы выбрать максимум силы тяги, руководствуясь следующими причинами:
-
вязкоупругие свойства опытного образца эластомера определяются в условиях статического и динамического нагружения, при которых общим параметром выступает тяговое усилие, развиваемое приводом;
-
значением тягового усилия устанавливается конечная деформация сжатием опытного образца эластомера. Осуществляя ступенчатое увеличение нагрузки с постоянным приращением напряжения (или деформации) на каждом шаге и производя остановку нагружения, можно наблюдать падение напряжения вследствие явления релаксации, отражающего процессы аккомодационной перестройки дефектной (дислокационной) структуры опытного образца эластомера под действием внешних и внутренних напряжений.
На рис. 1 приведены различные виды конструкций магнитных систем МЭП, выполненных с использованием магнитов намагниченных в радиальном направлении (рис. 1 а, б) и с магнитами, намагниченными в аксиальном направлении (рис. 2.1 в, г).
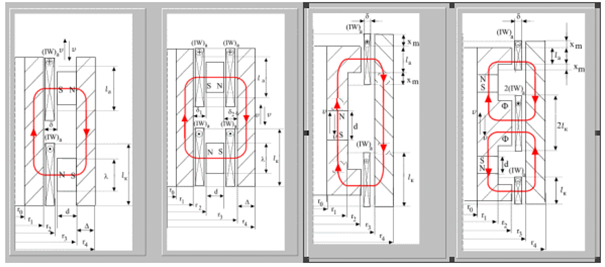
Рис. 1. Магнитные системы МЭП с магнитами, намагниченными в радиальном (а, б) и аксиальном направлении (в, г): а – МЭП с одним воздушным каналом; б – МЭП с двумя воздушными каналами; в – МЭП с одной парой полюсов; г – МЭП с двумя парами полюсов
Проведем оптимизацию МЭП по максимуму силы тяги со следующими допущениями:
1. Магнитное сопротивление стали мало, и им можно пренебречь вследствие значительного рабочего зазора на пути основного магнитного потока;
2. Высота активной части обмотки, расположенной на пути основного магнитного потока, определяется посредством операции умножения высоты полюса на значение поправочного коэффициента, учитывающего выпучивание магнитного потока в зазоре;
3. В пределах активной части обмотки индукция магнитного поля постоянна и равна среднему значению индукции в зазоре;
4. Плотность тока по сечению обмотки распределяется равномерно;
5. Магнитные потоки реакции и рассеяния не учитываются.
Принятые допущения при решении задачи оптимизации поэтапно могут сниматься результатами численного расчета магнитного поля привода с использованием МКЭ [3, 6].
Магнитная система МЭП с одним воздушным каналом и магнитами, намагниченными в радиальном направлении (рис. 1, а).
С учетом принятых допущений сила тяги МЭП определяется выражением:
![]() , (1)
, (1)
где ![]() – среднее значение магнитной индукции в воздушном зазоре;
– среднее значение магнитной индукции в воздушном зазоре; ![]() – средняя длина витка обмотки;
– средняя длина витка обмотки; ![]() – активная часть ампервитков обмотки в зоне действия основного магнитного потока;
– активная часть ампервитков обмотки в зоне действия основного магнитного потока; ![]() – высота активной части обмотки;
– высота активной части обмотки; ![]() – рабочий зазор;
– рабочий зазор; ![]() – коэффициент заполнения обмотки;
– коэффициент заполнения обмотки; ![]() – плотность тока;
– плотность тока; ![]() – площадь рабочего зазора;
– площадь рабочего зазора; ![]() – индукция в нейтральном сечении постоянного магнита;
– индукция в нейтральном сечении постоянного магнита; ![]() – площадь нейтрального сечения постоянного магнита.
– площадь нейтрального сечения постоянного магнита.
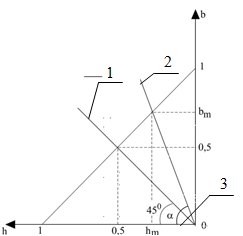
Рис. 2. К расчету магнитной цепи МЭП. 1 - характеристика размагничивания постоянного магнита; 2 - луч проводимости рабочего зазора ( λδ*=const); 3 - луч проводимости рабочего зазора для оптимальной геометрии магнитной системы МЭП λδ опт*=1.
Индукция в нейтральном сечении постоянного магнита определяется координатами точки пересечения кривой размагничивания магнита из материала фенибор и луча, соответствующего относительной проводимости воздушного зазора ![]() (рис. 2), которую можно определить путем решения системы уравнений [2, 4]:
(рис. 2), которую можно определить путем решения системы уравнений [2, 4]:
![]() , (2)
, (2)
где ![]() и
и ![]() – соответственно относительная напряженность и индукция;
– соответственно относительная напряженность и индукция; ![]() – коэрцитивная сила магнита;
– коэрцитивная сила магнита; ![]() – остаточная индукция;
– остаточная индукция; ![]() ;
; ![]() - проводимость рабочего зазора на пару полюсов;
- проводимость рабочего зазора на пару полюсов; ![]() – проводимость магнита на пару полюсов;
– проводимость магнита на пару полюсов; ![]() – длина магнита по оси намагничивания.
– длина магнита по оси намагничивания.
Решение системы (2) имеет вид:
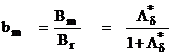 . (3)
. (3)
Подставляя решение (3) в выражение силы тяги (1), получим:
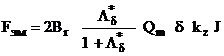 , (4)
, (4)
где ![]() .
.
Удельное тяговое усилие магнитоэлектрического привода определяется отношением силы тяги к суммарной массе активной части обмоток и постоянных магнитов, то есть:
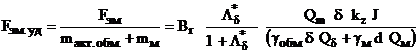 , (5)
, (5)
где ![]() – соответственно плотности используемых материалов для изготовления обмоточного провода и постоянного магнита, принимающие значения
– соответственно плотности используемых материалов для изготовления обмоточного провода и постоянного магнита, принимающие значения ![]() .
.
Используем обозначения ![]() и
и ![]() для преобразования выражения (5) к виду:
для преобразования выражения (5) к виду:
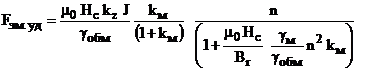 , (6)
, (6)
Из полученного выражения видно, что удельная сила тяги МЭП является функцией двух независимых переменных ![]() . Другие параметры в выражении (6) являются постоянными величинами, зависящими от характеристик используемых активных материалов и ограничений по плотности тока и коэффициенту заполнения обмотки при проектировании магнитной системы привода.
. Другие параметры в выражении (6) являются постоянными величинами, зависящими от характеристик используемых активных материалов и ограничений по плотности тока и коэффициенту заполнения обмотки при проектировании магнитной системы привода.
Для отыскания экстремума целевой функции приравняем нулю ее частные производные и решим систему уравнений для определения неизвестных ![]()
![]() . (7)
. (7)
При записи корней системы можно убедиться, что система уравнений в положительной полуплоскости пространства определена и имеет единственное решение:
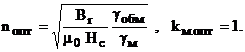 (8)
(8)
Подставляя полученные значения независимых переменных в выражение (6), можно найти максимальное значение удельной силы тяги для исследуемой магнитной системы МЭП:
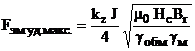 . (9)
. (9)
При этом оптимальное отношение площадей рабочего зазора и нейтрального сечения постоянного магнита будет:
 (10)
(10)
Числовой расчет отношения 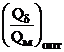 для различных марок сплавов постоянного магнита показывает, что его значение приближается к единице. Так, например, для марки сплава постоянного магнита
для различных марок сплавов постоянного магнита показывает, что его значение приближается к единице. Так, например, для марки сплава постоянного магнита ![]() типа фенибор [1] на основе железа (Fe), неодима (Nd) и бора (В) имеем:
типа фенибор [1] на основе железа (Fe), неодима (Nd) и бора (В) имеем: ![]()
![]() , удельная энергия постоянного магнита
, удельная энергия постоянного магнита ![]() отношение
отношение 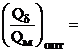 0,968, значение
0,968, значение ![]() . Для других марок сплавов постоянного магнита значения
. Для других марок сплавов постоянного магнита значения 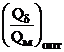 и
и ![]() приведены в табл. 1.
приведены в табл. 1.
Таблица 1
Оптимальные геометрические соотношения размеров магнитной системы МЭП
|
Марка сплава |
|
|
|
|
|
|
|
120 |
1.18 |
744 |
1.031 |
1.224 |
|
КСП 37 А |
72.5 |
0.9 |
500 |
1.099 |
1.304 |
|
КС 37 |
55 |
0.77 |
540 |
0.978 |
1.160 |
В оптимальной конструкции магнитной системы привода относительная индукция в нейтральном сечении магнита удовлетворяет условию:
![]() (11)
(11)
Магнитная система МЭП с двумя воздушными каналами и магнитами, намагниченными в радиальном направлении (рис. 1,б).
Тяговое усилие привода определяется выражением:
![]() . (12)
. (12)
Магнитная индукция в нейтральном сечении магнита согласно решению системы уравнений (2) будет:
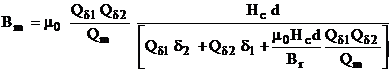 , (13)
, (13)
где ![]() – соответственно площади рабочих зазоров
– соответственно площади рабочих зазоров ![]()
Суммарную массу активных частей обмоток и постоянных магнитов можно записать в виде:
![]() . (14)
. (14)
Выразим удельную силу тяги привода через независимые переменные:
![]()
![]() ,
, ![]()
![]() (15)
(15)
Тогда после преобразований, принимая во внимание соотношения (15) – (18), получим:
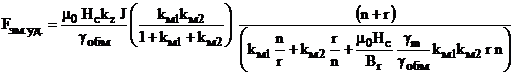 . (16)
. (16)
Найдем экстремум целевой функции (15), подчинив ее следующим условиям:
![]()
![]() (17)
(17)
Решая систему уравнений (16), найдем значения независимых переменных, обеспечивающие ему максимальное значение силы тяги:
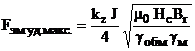 . (18)
. (18)
Критериальные соотношения имеют вид:
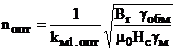 ,
, 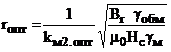 ,
, ![]() (19)
(19)
В оптимальной конструкции магнитной системы привода (рис. 1, б) выполняется равенство (11).
Магнитная система МЭП с магнитами, намагниченными в аксиальном направлении и одной парой полюсов (рис. 1, в).
Относительная магнитная проводимость рабочего зазора на пару полюсов определяется выражением:
![]() . (20)
. (20)
Подставляя выражение (23) в решение системы (6), преобразуем выражение тягового усилия (2.4) к виду:
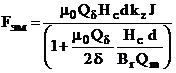 . (21)
. (21)
Введем независимые переменные:
![]()
![]()
![]() , (22)
, (22)
где ![]() – составляющие массы магнитной системы.
– составляющие массы магнитной системы.
Через независимые переменные удельная сила тяги определяется выражением:
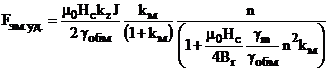 . (23)
. (23)
При отыскании экстремума целевой функции (23) используем условия (10). Из решения системы уравнений для определения оптимальных значений независимых переменных и подстановки их в выражение (26) получим выражение для определения максимального значения удельной силы тяги привода, идентичное выражению (21). Экстремум целевой функции достигается при оптимальных параметрах:
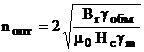 ,
, ![]() (24)
(24)
Для оптимальной геометрии магнитной системы привода справедливо соотношение (11).
Магнитная система МЭП с магнитами, намагниченными в аксиальном направлении и двумя парами полюсов (рис. 1, г).
Тяговое усилие, развиваемое приводом, вычисляется по формуле:
 . (25)
. (25)
Суммарная масса активных частей обмоток и постоянных магнитов будет:
![]() . (26)
. (26)
Введение независимых переменных (22) в выражение удельной силы тяги, определяемое по отношению (25) к (26), позволяет исследовать полученную функцию цели на экстремум. Максимальное значение удельной силы тяги находится из выражения, идентичного выражению (19). Для оптимальной геометрии магнитной системы привода выполняется равенство (11) и справедливы соотношения (24), при которых сила тяги достигает максимума.
Полученные соотношения из решения задачи оптимизации исследуемых магнитных систем МЭП по максимуму тягового усилия были использованы при разработке программы «Выбор» для ПК, написанной на языке виртуального программирования Borland Delphi 6.0 под управлением Microsoft Windows 2000.
Сравним результаты расчета оптимальных конструкций магнитных систем МЭП по программе «Выбор» на основе задания следующих исходных данных.
Максимальное электромагнитное усилие, Н…………………….100
Индукция в сердечнике, Тл………………………………………..1.6
Плотность тока в обмотке, ![]() …………………………………2е+6
…………………………………2е+6
Марка сплава постоянного магнита………………………………. Нм30Ди6Р
Остаточная индукция, Тл…………………………………………..1
Коэрцитивная сила, кА/м…………………………………………..750
Коэффициент заполнения по меди………………………………...0.4
Коэффициент рассеяния магнитного потока………………………1.1
Амплитуда хода якоря, м……………………………………………0.005
Радиус штока, м……………………………………………………...0
Соотношение массы внутренней обмотки к массе
магнита на пару полюсов (рис. 2., б)………..……………………0.4
Результаты расчета приведены в табл. 2
Таблица 2
Расчетные параметры магнитных систем МЭП, полученные при помощи программного обеспечения «Выбор»
|
№ п/п |
Параметр |
Ед. изм. |
Значение параметра |
|||
|
Рис. 1, а |
Рис. 1, б |
Рис. 1, в |
Рис. 1, г |
|||
|
1 |
Масса магнита на одну пару полюсов |
кг |
1.052 |
2.103 |
2.103 |
1.052 |
|
2 |
Масса активной части обмотки на одну пару полюсов |
кг |
1.052 |
1.052 |
2.103 |
1.052 |
|
3 |
Суммарная масса магнита и активной части обмотки |
кг |
4.207 |
4.207 |
4.207 |
4.207 |
|
4 |
Индукция в нейтральном сечении магнита |
|
0.500 |
0.578 |
0.5 |
0.5 |
|
5 |
Индукция в зазоре |
Тл |
0.530 |
во внут. 0.586 во внеш. 0.474 |
0.529 |
0.528 |
|
6 |
Высота магнита |
м |
|
|
|
|
|
7 |
Высота полюса |
м |
|
|
|
|
|
7 |
Длина магнита по оси намагничивания |
м |
|
|
|
|
|
8 |
Высота активной части обмотки |
м |
|
|
|
|
|
9 |
Высота обмотки |
м |
|
|
|
|
|
10 |
Толщина обмотки |
м |
|
|
|
|
|
11 |
Толщина стенки внешнего сердечника |
м |
|
|
|
|
|
12 |
Средний радиус магнита |
м |
0.053 |
0.052 |
0.023 |
0.018 |
|
13 |
Средний радиус обмотки |
м |
0.046 |
внут. обм. 0.046 внеш. обм 0.57 |
0.060 |
0.048 |
|
14 |
Радиус внутреннего сердечника магнитопровода |
м |
|
|
|
|
|
15 |
Радиус обмотки |
м |
|
внут. обм. внеш. обм.
|
внут. рад.
внеш. рад.
|
внут. рад.
|
|
16 |
Радиус магнита |
м |
|
|
|
|
|
17 |
Радиус внешнего сердечника магнитопровода |
м |
|
|
|
|
|
18 |
Удельное электромагнитное усилие |
|
23.770 |
23.765 |
23.77 |
23.77 |
|
19 |
Намагнич. сила акт. части обм. на одну пару полюсов |
А |
329.380 |
287.022 |
249.268 |
154.271 |
|
20 |
Проводимость магнита на одну пару полюсов |
Гн |
3.0е-6 |
2.96е-6 |
2.1е-7 |
1.6е-7 |
|
21 |
Относительная проводимость воздушного зазора |
|
1 |
1.373 |
1 |
1 |
Анализ результатов расчета оптимальных магнитных систем МЭП для испытаний вязкоупругих свойств эластомеров показывает, что для всех типов исследуемых магнитных систем привода при заданных технических условиях, конструкция которых удовлетворяет критерию оптимальности – максимуму тягового усилия, сохраняются одинаковые значения следующих основных параметров.
Суммарная масса постоянных магнитов и активной части обмотки, кг………………4.21
Оптимальное отношение массы активной части
обмотки к массе постоянных магнитов……………………………………………….… 1.0
Магнитная индукция в нейтральном сечении магнита ![]() , Тл…………..….0.58.
, Тл…………..….0.58.
Для создания максимального значения тягового усилия МЭП ![]() 100 Н (условие технического задания) конструктивно реализуемы магнитные системы МЭП с постоянными магнитами, намагниченными в радиальном направлении (рис. 1 а, б). В магнитной системе МЭП, приведенной на рис. 1 б, для обеспечения больших значений радиусов постоянного магнита (средний радиус магнита
100 Н (условие технического задания) конструктивно реализуемы магнитные системы МЭП с постоянными магнитами, намагниченными в радиальном направлении (рис. 1 а, б). В магнитной системе МЭП, приведенной на рис. 1 б, для обеспечения больших значений радиусов постоянного магнита (средний радиус магнита ![]() 0.052 м) наиболее эффективно применение постоянных магнитов, изготовленных в виде сегментов.
0.052 м) наиболее эффективно применение постоянных магнитов, изготовленных в виде сегментов.
Рецензенты:
Федоров В.К., д.т.н., профессор кафедры «Электротехники и электрификации» ОмГАУ им. П.А. Столыпина, г. Омск;
Харламов В.В, д.т.н., профессор, зав. кафедрой «Электрические машины и общая электротехника» Омского государственного университета путей сообщения, г. Омск.
Библиографическая ссылка
Татевосян А.А. ОПТИМИЗАЦИЯ ПАРАМЕТРОВ МАГНИТНЫХ СИСТЕМ ЛИНЕЙНОГО МАГНИТОЭЛЕКТРИЧЕСКОГО ПРИВОДА // Современные проблемы науки и образования. 2014. № 6. ;URL: https://science-education.ru/ru/article/view?id=15296 (дата обращения: 18.02.2026).



