Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Баклагин В.Н. 1

---

1 Инстиут водных проблем Севера, Карельский научный центр РАН

Показан пример численного решения уравнений Навье-Стокса методом маркеров и ячеек правосторонними разностными аппроксимациями, разработанных Харлоу и Уэлчем в 1965 году. Решение выполнено в простых физических переменных и не сводится к решению в виде переменных вихря и функции тока, что позволяет использовать полученное решение для моделирования жидкости со свободной поверхностью. Это используется при моделировании водных объектов (озер, рек, водохранилищ и других).Решаемые дифференциальные уравнения, описывающие движения жидкости, представлены нелинейными членами. Это делает их решение более трудоемким, однако полученные формулы позволяют адекватно описывать циркуляцию моделируемой жидкости. На основании полученных формул можно разрабатывать гидродинамические модели водоемов и использовать их для моделирования переноса тепла и примесей.

Статья в формате PDF

557 KB

метод маркеров и ячеек

численное решение

уравнения Навье-Стокса

моделирование водных объектов

1. Астраханцев Г. П., Меншуткин В. В., Петрова Н. А., Руховец Л. А. Моделирование экосистем больших стратифицированных озер – СПб: Наука, 2003. – 363 с.

2. Ментшуткин В. В., Показеев К. В., Филатов Н. Н. Гидрофизика и экология озер. Экология – М.: Физический факультет МГУ, 2004. – 280 с.

3. Роуч П. Вычислительная гидродинамика. – М.: Мир, 1980 – 616 с.

4. Самарский А.А. Теория разностных схем. – М: Наука, 1977 – 656 с.

5. HarlowF.H., WelchJ.E. Numericalcalculationoftime-dependentviscousincompressibleflowoffluidwithfreesurface. – Phys. ofFluids. – v. 8. - № 12.– Р. 2182-2189.

Перед моделированием движения жидкости ставится задача воспроизведения циркуляции жидкости в некой замкнутой или незамкнутой области, то есть нахождение модуля и направления скорости движения жидкости в каждой точке моделируемого объекта или системы. Существуют одномерные, двумерные и трехмерные модели, которые характеризуются количеством независимых координат, описывающих моделируемый объект или систему [2]. Наибольший практический интерес для воспроизведения циркуляции водных объектов, таких как озеро, водохранилище, река и другие, представляют трехмерные модели, которые могут быть реализованы в трехмерной прямоугольной (декартовой) системе координат.

Как правило, для задач, имеющих практическую ценность, при моделировании водных объектов или систем вода принимается как несжимаемаемая Ньютоновская жидкость. Такое допущение существенно упрощает уравнения Навье-Стокса, которые используют при моделировании движения жидкостей или газов.

Основная цель исследований – численно разрешить уравнения Навье-Сткоса в их нелинейном виде относительно простых физических величин с целью моделирования циркуляции жидкости для различных замкнутых и незамкнутых водных объектов, к которым можно отнести различные географические водные объекты.

Уравнения количества движения несжимаемой жидкости в консервативной форме в случае трехмерного пространства без участия внешних сил в безразмерных величинах можно записать в виде:

, (1)

, (2)

, (3)

где ,, – проекции неизвестной функции скорости на оси в декартовой прямоугольной трехмерной системе координат; – неизвестная функция давления; – число Рейнольдса.

Данные уравнения имеют в своем составе конвективные члены, представленные частными производными первого порядка по пространственным переменным, содержащимися в левой части. Эти члены уравнения учитывают перенос вихря, связанного с конвекцией и члены привносят в уравнение нелинейность. Также уравнение содержит диффузионные члены, представленные частными производными второго порядка по пространственным переменным в правой части уравнения, которые соответственно учитывают диффузионный перенос вихря.

Уравнение неразрывности для несжимаемой жидкости имеет вид:

. (4)

При моделировании жидкости систему уравнений (1)-(3) часто заменяют линеаризованными аналогами, выполнив замену мгновенной скорости на некую среднюю скорость потока в конвективных членах уравнения, тем самым упрощая данную систему. Среднюю скорость в данном случае можно считать постоянным коэффициентом, а, следовательно, уравнения становятся линейными. Такие линеаризованные аналоги имеют более простое численное решение. Такой упрощение было использовано при разработке математической модели Ладожского озера в работе [1].

Также в некоторых случаях используют упрощения, при которых нелинейные (конвективные) члены уравнения отбрасываются. В этом случае остаются только диффузионные члены уравнения и дальнейшее решение уравнений ведется без конвективных членов. Такое допущение также ведет к существенному упрощению численного решения этой системы уравнений. Однако модели, полученные таким образом, не всегда достаточно адекватно воспроизводят движение жидкости особенно для практических целей.

Произведем некоторые математические операции с исходными дифференциальными уравнениями (1)-(3), описывающими циркуляцию жидкости в трехмерном пространстве для получения формулы расчета неизвестной функции давления.

Продифференцируем систему уравнений по пространственным переменным: уравнение (1) – по , уравнение (2) – по , а уравнение (3) – по , и сложим полученные уравнения. Получим уравнение Пуассона [3], которое применяется для расчета функции давления в трехмерном пространстве:

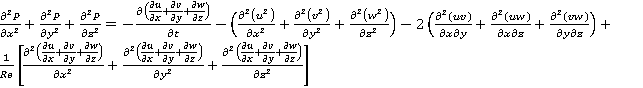. (5)

Приведем уравнение (5) к следующему виду, тождественно приравняв правую часть уравнения для простоты к члену , который в дальнейшем будет использован как «источниковый» член при нахождении сеточного аналога функции :

, (6)

где – дивергенция скорости; – оператор Лапласа.

Дивергенция скорости в принятых обозначениях имеет формулу:

. (7)

Согласно условию неразрывности дивергенция скорости равна нулю. В связи с этим можно было бы исключить члены, содержащие , из формулы (6) для расчета давления. Однако, поскольку для нахождения функции давления, уравнение (6) относительно будет решаться итерационными методами по указанным ниже причинам, то из-за недостаточной степени точности итерационного решения конечно-разностный аналог может быть не равен 0, то есть в узле сеточной области с номерами по осям трехмерной системы координат . Поэтому исключение из уравнения членов, содержащих , приведет к накоплению ошибки в уравнения количества движения, а также возможна и неустойчивость разностных аналогов данных уравнений в связи с накоплением этой ошибки, как указывается в работе [3]. Поэтому расчет членов, содержащих , несколько устраняет проблему. Выполняя расчеты с , имеется возможность приравнивать его сеточный аналог на следующем рассчитываемом временном шаге к нулю, тем самым не накапливая ошибку. В этом случае в конечно-разностном аналоге, аппроксимирующем производную дивергенции по времени необходимо принимать значение дивергенции на следующем временном слое равное нулю .

Для аппроксимации формулы (6) воспользуемся методом маркеров и ячеек, который был разработан авторами Харлоу и Уэлчем в 1965 году для решения дифференциальных уравнений численными методами. Описание метода представлено в работе [5].

Данный метод включают специфичную разностную сетку и специфичную структуру ячейки. Этот метод применяется для уравнений в простейших физических переменных, поэтому может быть применим для решения полученных уравнений. Трехмерная прямоугольная разностная сетка с позиционированием сеточных функций, используемая для аппроксимации непрерывных функций давления и компонентов скоростей, изображена на рисунке 1.

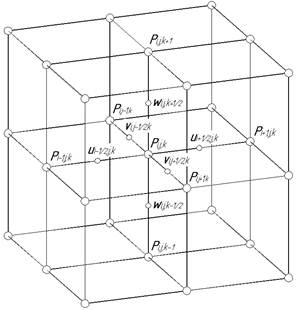
Рис. 1. Фрагмент разностная сетка для аппроксимации нелинейных членов уравнений

Особенность данной разностной сетки заключается в том, что сеточный аналог функции давления позиционируется в узлах трехмерной прямоугольной сетки (на рисунке такие узлы изображены крупными), а сеточные аналоги функций компонент скорости располагаются в дополнительных узлах (на рисунке они изображены мелкими), которые находятся посередине ребер трехмерной ячейки, образованной основными узлами сетки. Причем сеточный аналог проекции скорости на ось () располагается на ребре, параллельном оси , между узлами и . В свою очередь позиционируется на середине ребра, параллельного оси между узлами и , разделяя это ребро на две равных части, поэтому имеет номер узла по оси . Аналогичное позиционирование имеет и сеточный аналог проекции скорости на ось . Граничными узлами являются узлы, в котором позиционируется функция давления, значения скоростей задаются в этих узлах особенным образом, как будет показано ниже.

С учетом предложенной сетки конечно-разностный аналог дифференциального оператора , исходя из правил аппроксимирования «вперед» [4], имеет вид:

. (8)

Однако с учетом того, что , как было указано выше, для устранения невязки при итерационном решении получаемой системы алгебраических уравнений, конечно-разностный аналог в уравнении (6) примет вид:

. (9)

Конечно-разностные аналоги дифференциальных операторов ,, , , определяются следующими схемами, исходя из введенной сетки:

. (10)

. (11)

. (12)

. (13)

Значение можно определить осреднением по формуле:

. (14)

В связи с этим произведение величин можно представить как произведение средних величин:

. (15)

Заменим дифференциальный оператор правой части в уравнении (6) конечно-разностной схемой для расчета члена с учетом формул (10)-(13), (15):

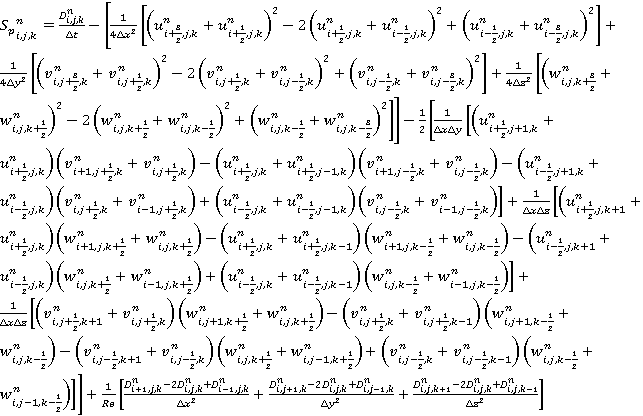. (16)

где конечно-разностный аналог дивергенции скорости имеет вид:

. (17)

После расчета члена в каждой ячейки сеточной области, необходимо произвести расчет сеточного аналога функции давления . Конечно-разностный аналог левой части уравнения (6) для расчета сеточного аналога функции давления имеет вид в результате центральной аппроксимации частных производных второго порядка:

. (18)

После решения уравнения (6) становится известным значения сеточной функции во внутренних узлах конечно-разностной сетки, которые необходимы для нахождения сеточных аналогов компонент скорости.

Аппроксимируем уравнения (1)-(3) конечно-разностными схемами с учетом введенной конечно-разностной сетки и выразим значение сеточного аналога функции компоненты скорости, получаемой на следующем временном шаге. На основании вышесказанного для уравнения (1) имеем:

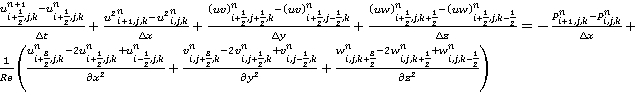. (19)

Отсюда выражая , получим явную одношаговую схему для расчета сеточного аналога функции на новом временном шаге:

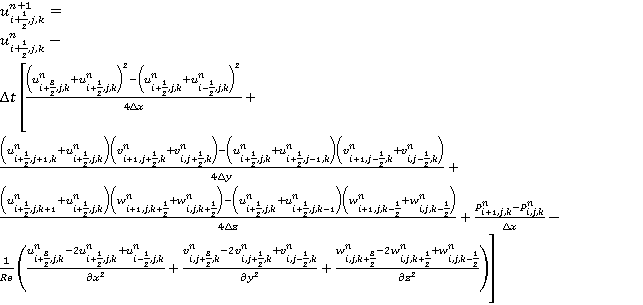. (20)

Аналогично получены формулы для расчета остальных сеточных аналогов функций компонентов скорости течения .

С помощью формул (16), (20) и аналогичных ей можно находить значения простых физических переменных в узлах используемой сеточной области. Полученные данные можно использовать при моделировании циркуляции жидкости в различных водных объектах и системах.

Вывод

Получены формулы, необходимые для моделирования водных объектов и систем, путем численного решения уравнений Навье-Стокса методом маркеров и ячеек. Решение произведено в простых физических переменных: давление и три проекции скоростей на трехмерной системе координат. При использовании соответствующих граничных и начальных условий данное решение позволит с высокой долей адекватности описывать различные водные объекты и системы.

Также следует отметить емкость полученных формул, что, безусловно, отразится на времени проведения расчетов, однако имеющиеся на настоящее время мощности вычислительных машин с многоядерными процессорами (кластеры и суперкомпьютеры) значительно ускорят процесс счета.

Работа выполнена при финансовой поддержке грантов РНФ 14-17-00740 «Озера России - диагноз и прогноз состояния экосистем при климатических и антропогенных воздействиях» и ПСР.1.11.1115А «Совершенствование деятельности в области преподавания географии в ВУЗе и в школе на основе внедрения новых информационных технологий».

Рецензенты:

Филатов Н.Н., д.г.н., профессор кафедры Географии Петрозаводского государственного университета, г. Петрозаводск;

Карпечко Ю.В., д.г.н., ведущий научный сотрудник лаборатории географии и гидрологии ИВПС КарНЦ РАН, г. Петрозаводск.

Библиографическая ссылка