Геофизический мониторинг атмосферных источников электромагнитного излучения, разработанный для регистрации и контроля движения грозовых разрядов, может быть использован для дистанционного отслеживания геодинамических процессов в земной коре [3, 4], связанных с формирующимися очагами землетрясений и активными разломами земной коры [6-9]. Важным вопросом при интерпретации аномалий электромагнитного излучения (ЭМИ) является разделение аномалий по типу источника излучения, что детально исследовано в работе [5].
Суммарный сигнал ЭМИ, можно представить в виде:
![]() , (1)
, (1)
где ![]() и
и ![]() импульсная аномальная (пики) и фоновые составляющие сигнала,
импульсная аномальная (пики) и фоновые составляющие сигнала, ![]() – случайный компонент. Причем, априори, функция источника сигнала не известна, т.е. для неё не известен тип модели, определяемой по (1).
– случайный компонент. Причем, априори, функция источника сигнала не известна, т.е. для неё не известен тип модели, определяемой по (1).
В линейной теории электромагнитных волн принята аддитивная модель исходного ряда наблюдений ЭМИ на основе принципа суперпозиции. Если временной ряд представляется в виде суммы соответствующих компонент, то полученная модель носит название аддитивной и имеет вид (без учета тренда и сезонной компоненты):
![]() , (2)
, (2)
где ![]() – уровни временного ряда.
– уровни временного ряда.
В данной работе представлены результаты имитационного моделирования разделения полей ЭМИ на основе статистического анализа временного ряда наблюдений, отражающих реальное состояние геофизической среды.
На рис. 1,2 показаны результаты наблюдений сигналов ЭМИ в периоды слабо возмущенного (рис. 1) и возмущенного (рис. 2) состояния геофизической среды. Качественно выделить фоновую составляющую ![]() в возмущенный день весьма проблематично.
в возмущенный день весьма проблематично.
Для отработки технологии разделения полей ЭМИ на фоновую ![]() и импульсную
и импульсную ![]() составляющие в модели (2) был создан имитационный файл в среде электронных таблиц Excel. Совокупный ряд исходных данных (2) был составлен из суммы рядов пиковых значений
составляющие в модели (2) был создан имитационный файл в среде электронных таблиц Excel. Совокупный ряд исходных данных (2) был составлен из суммы рядов пиковых значений ![]() , количество импульсов которых можно задавать произвольно и фоновой компоненты ряда в виде суммы периодической синусоидальной и случайной компонент ряда
, количество импульсов которых можно задавать произвольно и фоновой компоненты ряда в виде суммы периодической синусоидальной и случайной компонент ряда ![]() (рис.3). Суммарный ряд подвергался алгоритму выделения импульсов по методу Ирвина [2] (метод пиков), который используется в практике статистического анализа временных рядов с целью выделения аномальных уровней ряда.
(рис.3). Суммарный ряд подвергался алгоритму выделения импульсов по методу Ирвина [2] (метод пиков), который используется в практике статистического анализа временных рядов с целью выделения аномальных уровней ряда.
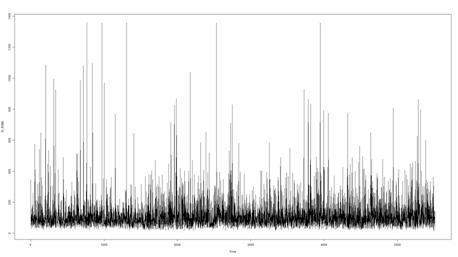
Рис. 1. Исходный ряд значений амплитуд сигналов ЭМИ в слабо возмущенный день 04.01.2013.
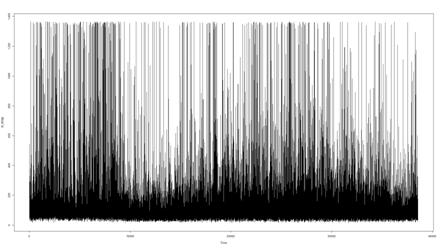
Рис. 2. Исходный ряд значений амплитуд сигналов ЭМИ в сильно возмущенный день 13.01.2013.
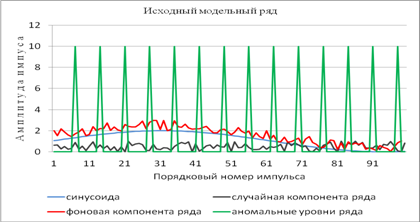
Рис. 3. Компоненты модельного ряда для имитации сигналов ЭМИ
Пусть имеется временной ряд ![]() . Метод Ирвина предполагает использование соотношения
. Метод Ирвина предполагает использование соотношения
![]() , (3)
, (3)
где 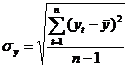 – стандартное отклонение,
– стандартное отклонение, 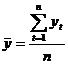 – среднее значение амплитуд, для оценки аномального приращения амплитуды последующего члена ряда
– среднее значение амплитуд, для оценки аномального приращения амплитуды последующего члена ряда ![]() в предположении, что предыдущий член ряда относится к фоновой составляющей сигнала
в предположении, что предыдущий член ряда относится к фоновой составляющей сигнала ![]() . Расчетные значения
. Расчетные значения ![]() сравниваются с табличными значениями критерия Ирвина
сравниваются с табличными значениями критерия Ирвина ![]() ; если какое-либо из них
; если какое-либо из них ![]() оказывается больше табличного
оказывается больше табличного ![]() , то соответствующее значение
, то соответствующее значение ![]() уровня
уровня ![]() ряда считается аномальным. Значения критерия Ирвина для уровня значимости
ряда считается аномальным. Значения критерия Ирвина для уровня значимости ![]() приведены в таблице 1.
приведены в таблице 1.
Таблица 1
Значения критических значений ![]() для уровня значимости
для уровня значимости ![]()
|
|
2 |
3 |
10 |
20 |
30 |
50 |
100 |
|
|
2.8 |
2.8 |
1.5 |
1.3 |
1.2 |
1.1 |
1 |
Для практических расчетов при известной длине реализации ![]() можно использовать аналитическое выражение для определения критических значений
можно использовать аналитическое выражение для определения критических значений ![]() , для которой погрешность аппроксимации меньше 1%:
, для которой погрешность аппроксимации меньше 1%:
![]() , (4)
, (4)
где ![]() .
.
Численные эксперименты показали следующее: во-первых, для одиночного пика (аномального уровня) ![]() относительно фонового уровня
относительно фонового уровня ![]() следующий член ряда
следующий член ряда ![]() также интерпретируется как аномальный, хотя амплитуда его импульса сравнима с фоновым значением. Во-вторых, эта же погрешность будет присутствовать при наличии в исходном ряде нескольких аномальных уровней
также интерпретируется как аномальный, хотя амплитуда его импульса сравнима с фоновым значением. Во-вторых, эта же погрешность будет присутствовать при наличии в исходном ряде нескольких аномальных уровней ![]() ,
, ![]() , …
, …![]() . В данном случае, за аномальный уровень рада будет принят первый аномальный
. В данном случае, за аномальный уровень рада будет принят первый аномальный ![]() и следующий за серией аномалий фоновый уровень
и следующий за серией аномалий фоновый уровень ![]() . Все промежуточные аномалии
. Все промежуточные аномалии ![]() , …,
, …, ![]() будут отнесены к фоновой составляющей ряда. Это приведет к искажению (завышению) огибающей фоновой компоненты (рис. 4).
будут отнесены к фоновой составляющей ряда. Это приведет к искажению (завышению) огибающей фоновой компоненты (рис. 4).
При интерактивном способе разделения уровней ряда фиктивные аномальные уровни отбраковываются оператором. В задачах автоматизированной обработки данных ряды пиков осложняются пропорциональным количеством значений фоновых компонент.
Для тех случаев, когда количество пиков превышает 50% от общего количества значений ряда и тем более для подряд стоящих пиков сформированный ряд фоновых данных осложняется пиковой компонентой (рис.5). Видимо эти погрешности до сих пор не позволили методу Ирвина найти достаточно широкое применение в практике статистических исследований временных рядов.
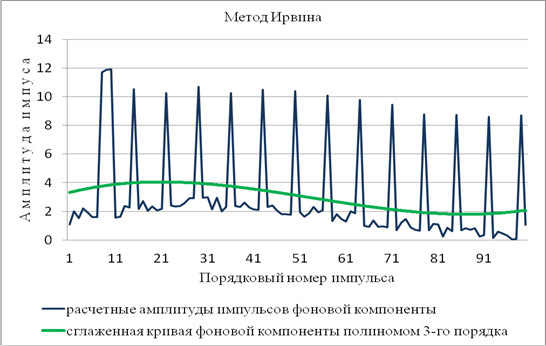
Рис. 4. Иллюстрация осложнения фоновой компоненты ряда аномальными уровнями при использовании метода Ирвина
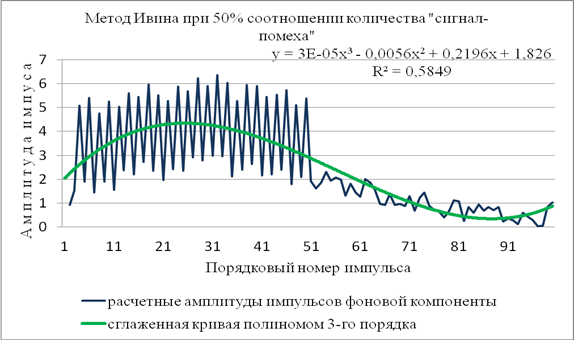
Рис. 5. Осложнение фоновой составляющей имитационного ряда при 50% соотношении пиковых и фоновых компонент
В результате численного моделирования различных соотношений «сигнал - помеха» была разработана методика в виде модифицированного метода Ирвина для адекватного разделения аномальных (пиковых) и фоновых уровней ряда. Данная задача, как было указано выше, актуальна для систем электромагнитного мониторинга грозовых разрядов и поиска различных источников электромагнитного излучения тектонической природы.
Для исключения указанных погрешностей метода Ирвина было разработано три варианта расчетов для разделения уровней рада, применение которых обосновано сложностью соотношений «сигнал-помеха» в реальных экспериментальных данных, например, как это показано на рис. 1, 2.
В простейшем случае, для выделения одиночных пиков положительно определенного ряда к условию Ирвина (3) добавляется условие не отрицательности разности ![]() , т.е.
, т.е. ![]() . Все аномальные уровни в фоновой компоненте ряда заменяются значениями по формуле параболического интерполирования:
. Все аномальные уровни в фоновой компоненте ряда заменяются значениями по формуле параболического интерполирования:
![]() , (5)
, (5)
где ![]() члены ряда фоновой компоненты, предшествующие аномальному уровню
члены ряда фоновой компоненты, предшествующие аномальному уровню ![]() . Так как первый член ряда может быть с аномальной амплитудой, то в начале ряда проставляются три дополнительных члена ряда с минимальной амплитудой. Результаты численного моделирования по данному алгоритму показаны на рис. 6.
. Так как первый член ряда может быть с аномальной амплитудой, то в начале ряда проставляются три дополнительных члена ряда с минимальной амплитудой. Результаты численного моделирования по данному алгоритму показаны на рис. 6.
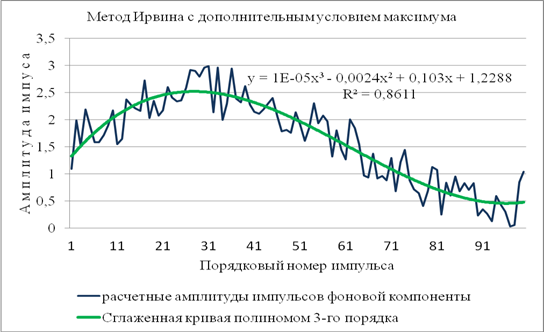
Рис. 6. Выделение фоновой составляющей имитационного ряда при наличии одиночных пиковых компонент с дополнительным условием не отрицательности разности сравниваемых амплитуд последовательных членов ряда
Сравнение с результатами расчетов с применением простого алгоритма Ирвина (рис. 4) наглядно показывает необходимость введения в алгоритм дополнительного условия не отрицательности разности ![]() .
.
При увеличении количества аномальных уровней до 50% замена пиковых значений по формуле (5) приводит к осложнению фоновой компоненты усредненными значениями амплитуд аномальных уровней (рис. 5). В данном случае применяется алгоритм последовательного исключения аномальных уровней.
Амплитуды сигнала аномальных уровней в фоновой компоненте заменяются по формуле (5) с возвратом на начало цикла расчетов. При этом значение стандартного отклонения ![]() рассчитывается для первоначального ряда и при повторных расчетах принимается за константу.
рассчитывается для первоначального ряда и при повторных расчетах принимается за константу.
Данный алгоритм позволяет адекватно разделять фоновую и импульсную компоненты, однако требует большего времени для расчетов, так как в массиве данных за сутки накапливается до 80000 импульсов и более, что приведет к задержке отображения результатов в реальном времени в системах автоматизированного мониторинга.
Для случаев возмущенного состояния геофизической среды (см. рис. 2) разработан алгоритм с построением вариационного ряда с возрастающими амплитудами сигнала. Для ![]() = (20-40)% от общего количества членов вариационного ряда рассчитывается стандартное отклонение
= (20-40)% от общего количества членов вариационного ряда рассчитывается стандартное отклонение ![]() и применяется метод Ирвина до появления первого аномального уровня
и применяется метод Ирвина до появления первого аномального уровня ![]() . Максимальное значение из первых (k-1) уровней вариационного ряда принимается за граничное значение фоновой компоненты, по которому производится разделение компонент исходного ряда.
. Максимальное значение из первых (k-1) уровней вариационного ряда принимается за граничное значение фоновой компоненты, по которому производится разделение компонент исходного ряда.
Численное моделирование с использованием данных натурного эксперимента показало, что, если в исходном ряде присутствует только две компоненты, то фоновая компонента выделяется из исходного ряда без искажений. При наличии нескольких источников ЭМИ метод чувствителен к выбору количества членов вариационного ряда для расчета ![]() . Это может привести к пропуску аномальных источников сигнала либо к выделению мнимых источников (ошибки первого и второго родов). Для исключения данных погрешностей в системе автоматического мониторинга предполагается производить расчеты с использованием различных процентных выборок
. Это может привести к пропуску аномальных источников сигнала либо к выделению мнимых источников (ошибки первого и второго родов). Для исключения данных погрешностей в системе автоматического мониторинга предполагается производить расчеты с использованием различных процентных выборок ![]() из вариационного ряда для расчета
из вариационного ряда для расчета ![]() и применения метода Ирвина. Адекватность модели во всех случаях проверяется по статистическим характеристикам остаточного ряда [1]. Проведенные расчеты для двух дней с различным состоянием возмущенности геофизической среды (рис.1, 2) показали сходимость моделей фоновых компонент, выделенных по методам исключения пиков и построения вариационного ряда при
и применения метода Ирвина. Адекватность модели во всех случаях проверяется по статистическим характеристикам остаточного ряда [1]. Проведенные расчеты для двух дней с различным состоянием возмущенности геофизической среды (рис.1, 2) показали сходимость моделей фоновых компонент, выделенных по методам исключения пиков и построения вариационного ряда при ![]() = (35 – 45)%.
= (35 – 45)%.
Рецензенты:
Омельяненко А.В., д.т.н., профессор, главный научный сотрудник лаборатории инженерной геокриологии Института мерзлотоведения им. П.И.Мельникова СО РАН, г. Якутск;
Имаев В.С., д.г.-м.н., профессор, гл. научный сотрудник Института земной коры СО РАН, г.Иркутск.
Библиографическая ссылка
Трофименко С.В., Трофименко С.В., Маршалов А.Я., Гриб Н.Н., Колодезников И.И. МОДИФИКАЦИЯ МЕТОДА ИРВИНА ДЛЯ ВЫЯВЛЕНИЯ АНОМАЛЬНЫХ УРОВНЕЙ ВРЕМЕННЫХ РЯДОВ: МЕТОДИКА И ЧИСЛЕННЫЕ ЭКСПЕРИМЕНТЫ // Современные проблемы науки и образования. 2014. № 5. ;URL: https://science-education.ru/ru/article/view?id=15130 (дата обращения: 09.02.2026).



