В настоящее время исследования в области повышения транспортно-эксплуатационных качеств лесотранспортных машин (ЛТМ) чаще всего направлены на изучения динамических процессов в узлах и агрегатах. Однако специфические условия эксплуатации лесотранспортных машин не позволяют в полной мере использовать богатый опыт, накопленный в теории колебаний автомобилей. Поэтому требования к математической модели колебаний колесной ЛТМ определяются задачами, связанными как с исследованием колебаний корпуса машины, так и с процессами, которые возникают при взаимодействии ходовой частью с опорной поверхностью лесных дорог.
Целью данной работы является разработка математической модели колебаний корпуса и ходовой части колесной ЛТМ с учетом взаимодействия ходовой части с деформируемой опорной поверхностью лесных дорог.
Методы исследования
Анализ эксплуатационных характеристик современных ЛТМ позволил сформулировать основные требования к математической модели:
-
моделирование колебаний корпуса и пневмоколес ЛТМ должно производиться по трем угловым и трем линейным координатам для каждого элемента машины;
-
в модели должно быть учтено влияние связей ходовой части с опорной поверхностью, между отдельными элементами ЛТМ и лесным грузом;
-
модель должна быть универсальной, то есть позволяющей решать вопросы поведения ЛТМ в зависимости от типа опорной поверхности, от типа ходовой части, количества и параметров упругих и диссипативных элементов подвески;
-
модель должна оценивать проходимость ЛТМ по лесным дорогам в конкретных эксплуатационных условиях;
-
модель должна учитывать изменения физико-механических параметров опорной поверхности при взаимодействии с ней ходовой части ЛТМ;
-
модель должна оценивать степень влияния ходовой части ЛТМ на лесную среду.
Учитывая сложность поставленной задачи, математическая модель ЛТМ разрабатывалась в два этапа. На первом этапе была получена линеаризованная модель колебаний корпуса ЛТМ при движении ее с лесным грузом. Полученная модель и результаты ее решения подробно рассмотрены в работе [5].
На втором этапе в разработанную модель колебаний лесотранспортной машины были внесены изменения, для учета взаимодействия ходовой части с опорной поверхностью. Расчетная схема ЛТМ для моделирования представлена на рисунке 1.
На рисунке приведены следующие обозначения: колебания подрессоренных масс происходят по координатам х3, у3 , z2, неподрессоренных масс от мостов и пневмоколес по координатам х2, у2 , z2 . Параметры опорной поверхности задаются по координатам х1, у1 , z1 .
Поступательное движение ЛТМ по координате х реализовано за счет приложения крутящего момента Мкр со стороны двигателя на пневмоколеса, с тангенциальной жесткостью С��y2. Силовое взаимодействие с пневмошиной ЛТМ представлено в виде упругих cqij и диссипативных kqij свойств опорной поверхности. При поступательном движении ЛТМ происходит деформация опорной поверхности, что вызывает появление момента сопротивления качения пневмошины Мс. Для повышения точности результатов моделирования деформация опорной поверхности, задается нелинейными физико-механическими характеристиками, рассмотренными в работах [2-4,7]. Жесткость подвески в i-ом элементе ходовой части на j-ой стороны обозначена через - cji. Коэффициент сопротивления в i-ом элементе ходовой части на j-ой стороны через - kji. Силовое взаимодействие от пакета длинномерного лесного груза (пачка сортиментов) представлено в виде - Pn.
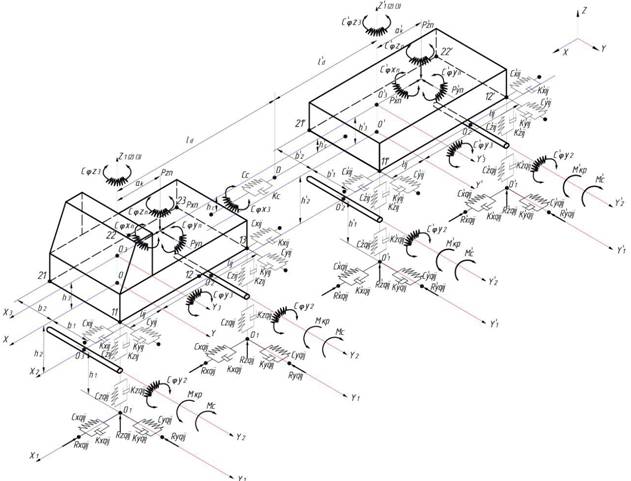
Рис.1. Расчетная схема колебаний корпуса и ходовых частей ЛТМ с учетом взаимодействия с опорной поверхностью
Принимая в качестве обобщенных координат, канонические координаты квадратичной формы кинетической энергии, традиционно уравнение колебаний ЛТМ записывают в виде уравнения Лагранжа [1]. Способы решения уравнений такого вида в настоящее время подробно разработаны. Сложность в представлении функции взаимодействия пневмоколес ЛТМ с опорной поверхностью и значительное количество элементов, участвующих в динамических процессах, привела к неоправданному усложнению модели, а ее решение описанным выше традиционным способом требует большого объема вычислительных процедур. В нашем случае математическая модель представляет систему, состоящую из 42-х дифференциальных уравнений второго порядка, описывающая механическую систему взаимодействия ЛТМ с опорной поверхностью (см. рисунок 1).
С целью оптимизации процедуры решения математической модели и получения нового научного знания рассмотрим метод, основанный на ином подходе к решению динамических задач.
Речь идет о создании математической модели колебаний корпуса ЛТМ на базе теории графов, с использованием объектно-ориентированного подхода к построению модели.
Если обозначить обобщенные координаты Лагранжа через q, а координаты инерционных, внутренних и внешних взаимодействий системы через ϑ, η, χ, то уравнение колебаний системы можно представить в виде
(1)
где 
– матрица приведенных коэффициентов инерции, 
;
– матрица смежности приведенных коэффициентов диссипации между элементами системы, 
– матрица смежности приведенных коэффициентов жесткости между элементами системы, 
R – диагональная матрица коэффициентов диссипации системы;
C – диагональная матрица коэффициентов жесткости системы;
– вектор приведенных внешних сил взаимодействия, 
;
X – вектор внешних сил, действующих на систему.
Для оптимизации расчетов и составления программного решения примем в качестве обобщенных координат канонические координаты квадратичной формы кинетической энергии системы 
, и матрицы в уравнении 1 примут вид:
Полученное решение уравнения соответствует основным положениям, представленных в широко известных работах В.Л. Вейца, и их удобнее рассматривать в форме графов [1, 8].
Результаты
Представленное линейное уравнение соответствует многодольному графу и позволяет организовать совершенно новую структуру модели колебаний ЛТМ.
В дальнейшем уравнение динамических колебаний корпуса ЛТМ, с учетом взаимодействия с опорной поверхностью удобнее представить в виде графа, изображенного на рисунке 2. На котором представлены лишь общие связи между элементами модели ЛТМ.
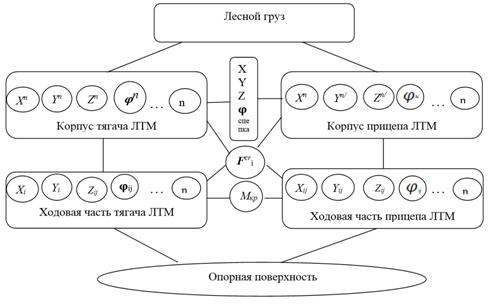
Рис. 2. Структура графа динамических колебаний корпуса ЛТМ с учетом взаимодействия с опорной поверхностью
Следует отметить, что вершина суграфа «Опорная поверхность» характеризует не только внешнее взаимодействие с объектом, но и сама является результатом решения модели для низшего уровня, по оценке степени влияния динамических колебаний ЛТМ на опорную поверхность.
С целью получения обозримости полного графа модели колебаний ЛТМ используем модели, построенные по модульному принципу.
Как показано в работах [5,6], модульный принцип построения подобных моделей позволяет использовать характеристики элементов корпуса ЛТМ, элементов ходовой части и физико-механические параметры опорной поверхности непосредственно, для создания однотипных классов, уровней и модулей.
Создание классов базируется на описании особенности колебаний элементов ЛТМ, а также их взаимодействия и характера внутренних и внешних связей с более высокими уровнями колебаний элементов ЛТМ.
Модули включают в себя элементы, определяющие структуру и особенности решения уравнения 1 с учетом внутренних и внешних связей.
Примером модуля является граф, описывающий колебания колес и оси ходовой части ЛТМ, изображенный на рисунке 3.
Однотипные модули связаны элементами взаимодействия или их комбинациями. Связанные таким образом, они представляют собой модули более высокого уровня. Примером модуля более высокого уровня является модуль колебаний элементов кузова ЛТМ.
Так как система уравнений, графы структуры и алгоритмические программы содержат уровни, то это позволило при вычислительных процедурах, давать их описание только один раз, а затем это описание использовать для клонирования и наследования во всех остальных модулях.
Таким образом каждый элемент описан в алгоритмической программе один раз, в виде класса. Все объекты, полученные при помощи одного класса, собраны в доли графа, для их дальнейшего сканирования и обработки [5, 9].
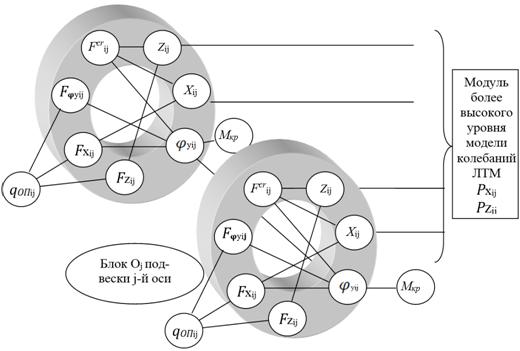
Рис. 3. Граф базового модуля модели колебаний колес и оси ходовой части ЛТМ:
Xij, Zij, φyij – координаты колебаний j-го пневмоколеса i-ой стороны; Fхij - упругодиссипативные свойства j-го пневмоколеса i-ой стороны по координате X при взаимодействии с опорной поверхностью; Fzij - упругодиссипативные свойства j-го пневмоколеса i-ой стороны по координате Z при взаимодействии с опорной поверхностью; F��yij - упругодиссипативные свойства j-го пневмоколеса i-ой стороны по координате ��y при взаимодействии с опорной поверхностью; Fcrij- кориолисово ускорение j-го пневмоколеса i-ой стороны; Мкр - крутящий момент от двигателя ЛТМ; Рхij - упругодиссипативные свойства подвески j-го пневмоколеса i-ой стороны по координате X; Рzij - упругодиссипативные свойства подвески j-го пневмоколеса i-ой стороны по координате Z; qОПij - функция от координаты и свойств опорной поверхности при взаимодействии с ней j-го пневмоколеса i-ой стороны.
Заключение
На рисунке 4 представлено решение математической модели по оценке воздействия ЛТМ на деформируемую опорную поверхность в момент начала поступательного движения по координате х.
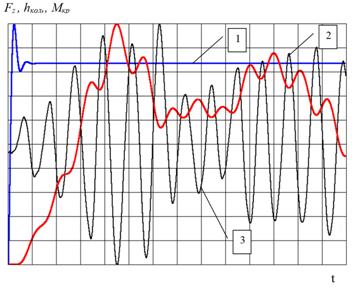
Рис. 4. Воздействие на опорную поверхность в момент начала поступательного движения (левая сторона ЛТМ):
1- Мкр - крутящий момент от двигателя ЛТМ;
2 - hкол - глубина колеи при проходе ЛТМ;
3- Fz - величина усилия на опорную поверхность со стороны пневмоколеса в вертикальной плоскости по координате z.
Разработанная модель, помимо оценки динамических колебаний ЛТМ, позволила оценить и степень влияния на опорную поверхность лесной дороги в момент начала поступательного движения и в установившемся режиме.
Рецензенты:
Кошкаров Е.В., д.э.н., к.т.н., старший научный сотрудник, ООО «Научно-исследовательский центр «ГИПРОДОРНИИ», г. Екатеринбург.
Силуков Ю.Д., д.т.н., профессор, ФГБОУ ВПО «Уральский государственный лесотехнический университет», г. Екатеринбург.
Библиографическая ссылка
Кручинин И.Н. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ЛЕСОТРАНСПОРТНОЙ МАШИНЫ ДЛЯ ИССЛЕДОВАНИЯ ВЗАИМОДЕЙСТВИЯ ХОДОВОЙ ЧАСТИ С ДЕФОРМИРУЕМОЙ ОПОРНОЙ ПОВЕРХНОСТЬЮ // Современные проблемы науки и образования. – 2014. – № 5. ;URL: https://science-education.ru/ru/article/view?id=15129 (дата обращения: 20.04.2024).