Ферромагнитные материалы с памятью формы (ФМПФ) позволяют реализовать большие обратимые деформации за счет перестройки мартенситной доменной структуры в магнитном поле [2]. Этот эффект можно выгодно использовать для создания исполнительных устройств, в том числе короткоходных линейных приводов. Кроме того, существует зависимость между деформацией ФМПФ и его магнитной проницаемостью, что позволяет получать информацию об относительном удлинении активного элемента привода. Однако создание исполнительных устройств на основе ФМПФ сдерживается из-за необходимости создания для обеспечения больших деформаций магнитных полей с напряженностью до 600 кА/м и значительной зависимостью параметров ФМПФ от температуры [3]. В этой связи разработка исполнительных устройств с учетом указанных особенностей является актуальной задачей.
Цель работы: разработка математического инструментария для определения оптимальных параметров магнитной системы исполнительного устройства на основе ферромагнитного материала с памятью формы, предназначенных для промышленных систем управления.
Материал и методы исследований: методы теории электромагнитного поля, теории электрических и магнитных цепей, элементы теории планирования эксперимента.
Результаты и обсуждение
Основной сложностью при разработке исполнительных устройств (приводов) на основе ФМПФ является разработка магнитной системы для создания требуемой напряженности магнитного поля. В качестве концентраторов поля используются ферромагнитные сердечники, вносящие значительную индуктивность в магнитную цепь, тем самым значительно увеличивая время срабатывания устройства [4,5]. Отказ от ферромагнитного сердечника магнитной системы позволяет значительно уменьшить размеры устройства. Однако возрастают требования к силе намагничивающего тока и тепловым режимам их работы. Поэтому целесообразно использование импульсного режима намагничивания. В этом случае ток в намагничивающей катушке не создает условия перегрева элементов устройства. В частности, активного элемента, изготовленного из ФМПФ.
Предлагается исполнительное устройство, реализующее этот подход. Структурная схема устройства (рис.1) содержит распределенную намагничивающую катушку (1), подключенную к многоканальному источнику тока управляемого напряжением (МИТУН), активный элемент (2), устройство управления (УУ) и измерительный преобразователь (ИП). Намагничивающая катушка состоит из шести сегментов, причем каждый сегмент подключен к МИТУН, что дает возможность перемагничивать как весь активный элемент, так и отдельную его часть. Включение ИП в состав устройства позволяет получать информацию о деформации элемента, за счет измерения магнитной проницаемости материала. УУ обеспечивает генерацию управляющих сигналов для МИТУН в зависимости от входного сигнала (3) и передает информацию о состоянии привода (4).
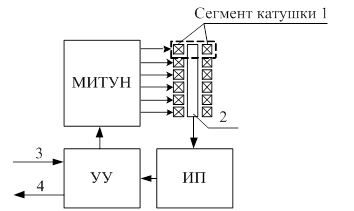
Рис. 1. Структурная схема исполнительного устройства
Для определения оптимальных параметров магнитной системы исполнительного устройства необходимо учитывать зависимость сопротивления сегмента катушки и количество витков в сегменте от площади ее сечения, ограничения связанные с размерами магнитной системы и мощностью, рассеиваемой на катушке.
Распределенная катушка должна обеспечивать намагничивание заданного фрагмента активного элемента привода до заданного уровня, от 200 до 600 кА/м, минимально возможное выделение тепла при намагничивании, высокую скорость намагничивания элемента и простоту реализации УУ.
После выбора материала активного элемента исполнительного устройства и определения необходимого числа сегментов распределенной катушки решается полевая задача для определения распределения магнитного поля внутри материала. На основании полученных данных уточняются геометрические размеры сегментов катушки, количество таких сегментов и их взаимное расположение, а также необходимое число ампер-витков. На рисунке 2 представлена геометрическая модель магнитной системы.
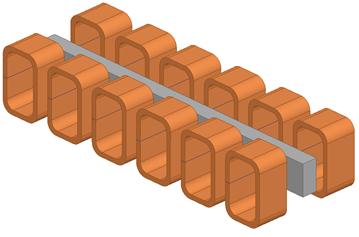
Рис. 2. Внешний вид намагничивающей системы
Общая геометрия сегмента катушки выбиралась из следующих соображений:
-
минимально возможные размеры, при заданном количестве витков;
-
обеспечение требуемой напряженности магнитного поля в активном элементе ФМПФ.
В расчетах используется зависимость между диаметром провода и сопротивлением катушки, напряжением питания и силой тока в цепи. Для активного элемента, имеющего размеры: 1x2x19 мм, геометрические размеры сегмента катушки: A=3,5; B=2; H=2; и R=B/4 (рис. 3). Параметр катушки C зависит от количества слоев намотки, при этом он ограничен значением LS, из-за общей геометрии системы.
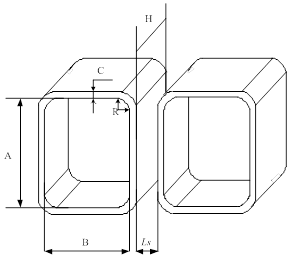
Рис. 3. Размеры сегмента катушки
Результатом решения полевой задачи является определение значения магнитодвижущей силы J, необходимой для перемагничивания фрагмента активного элемента, J = I•ω = = 10000ампер-витков.
Задавшись начальными условиями и решив систему уравнений:
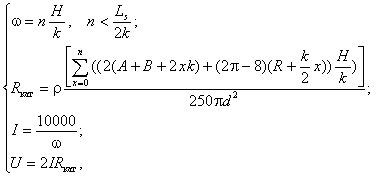 (1)
(1)
определяются оптимальные параметры магнитной системы. В системе (1): n – количество слоев в сегменте катушки, ω – количество витков в сегменте катушки; k – диаметр сечения проводника; I – ток в сегменте катушки; U– напряжение на сегменте катушки; Rкат – сопротивление сегмента катушки; r – плотность материала проводника.
Результаты расчета параметров магнитной системы сведены в табл. 1. Для упрощения реализации системы управления намагничиванием, за счет использования доступной элементной базы и обеспечения требуемых геометрических размеров целесообразно создание магнитной системы со следующими параметрами: k=0,2 мм; ω=66 витков; Rкат=0,90 Ом; U=138 В.
Табл. 1. Результаты расчета параметров магнитной системы
|
k, мм |
ω |
I,А |
Rкат,Ом |
U,В |
|
0,30 |
31 |
318 |
0,18 |
57 |
|
0,24 |
47 |
212 |
0,42 |
92 |
|
0,20 |
66 |
152 |
0,90 |
138 |
|
0,17 |
88 |
114 |
1,7 |
194 |
|
0,14 |
113 |
88 |
2,9 |
262 |
|
0,12 |
141 |
71 |
4,8 |
344 |
|
0,10 |
172 |
58 |
7,6 |
440 |
Для исследования процесса импульсного перемагничивания активного элемента исполнительного устройства предлагается следующая математическая модель. Эквивалентную схему магнитной системы, в которой находится сегмент распределенной катушки, представим в виде последовательно соединенных: источника ЭДСU0; ключа K и катушки, состоящей из сопротивления R и индуктивности L (рис. 4). В качестве источника ЭДС используем конденсатор, в теории с бесконечной емкостью, на практике с емкостью, достаточной для обеспечения импульса тока с заданными параметрами.
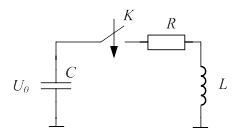
Рис. 4. Эквивалентная схема магнитной системы
Характеристическое уравнение для данной цепи будет иметь следующий вид [1]:
![]() . (2)
. (2)
После нахождения корней уравнения (2) рассчитывается ток в сегменте катушки и напряжение на конденсаторе:
![]() ; (3)
; (3)
![]() ,
,
где![]() ;U0 – напряжение на конденсаторе до коммутации.
;U0 – напряжение на конденсаторе до коммутации.
В зависимости от значения корней уравнения (2) ток достигнет максимального значения через время
![]() .
.
Задавшись значением емкости C = 100 мкФ и используя уравнение (3), получили график переходного процесса, приведенного на рисунке 5. Из графика следует, что заданную амплитуду импульса тока можно создавать в течение 20 мкс.
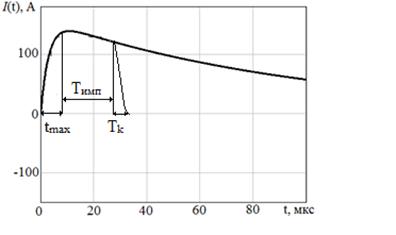
Рис. 5. Переходной процесс при разряде конденсатора на сегмент катушки
Выбрав значение длительности импульса Tимп , достаточное для перемагничивания активного элемента исполнительного устройства, можно определить фактическую длительность намагничивающего импульса в сегменте распределенной катушки:
![]() ,
,
где Tк – время срабатывания ключа K,Tк>>tmax. Фактическая длительность импульса Tн, при использовании транзистора IRG4PH40UD2-E в качестве ключа, составляет 20,45 мкс.
Заключение
Разработана магнитная система исполнительного устройства на основе ФМПФ и предложена методика расчета ее параметров, учитывающая зависимость сопротивления сегмента намагничивающей катушки и количество витков в сегменте от площади ее сечения, ограничения, связанные с размерами магнитной системы и мощностью рассеиваемой на катушке. Выбраны оптимальные размеры сегментов катушки, позволяющие при минимально возможных размерах получить требуемый уровень напряженности создаваемого магнитного поля. Предложена математическая модель для исследования процесса импульсного перемагничивания активного элемента устройства, определены параметры намагничивающего импульса.
Результаты работы получены при поддержке проекта № 2833 «Теоретические основы моделирования, диагностики и информационного обеспечения сложных технических систем», выполняемого в рамках базовой части государственного задания № 2014/143, с использованием оборудования ЦКП «Диагностика и энергоэффективное электрооборудование» ЮРГПУ(НПИ) им. М.И. Платова.
Рецензенты:
Елсуков В.С., д.т.н., профессор, профессор кафедры «Автоматика и телемеханика», ФГБОУ ВПО «Южно-Российский государственный политехнический университет (НПИ) имени М.И. Платова», г. Новочеркасск;
Савелов Н.С., д.т.н., доцент, профессор кафедры «Автоматика и телемеханика»,
ФГБОУ ВПО «Южно-Российский государственный политехнический университет (НПИ) имени М.И. Платова», г. Новочеркасск.
Библиографическая ссылка
Гречихин В.В., Кудря А.В., Кудря Н.А. ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ МАГНИТНОЙ СИСТЕМЫ ИСПОЛНИТЕЛЬНОГО УСТРОЙСТВА НА ОСНОВЕ МАТЕРИАЛА С ПАМЯТЬЮ ФОРМЫ // Современные проблемы науки и образования. 2014. № 5. ;URL: https://science-education.ru/ru/article/view?id=15077 (дата обращения: 01.03.2026).



