Рассмотрим модель механической системы, максимально приближенную к движениям человека, в связи с чем возникает необходимость моделирования шарниров-суставов, позволяющих осуществлять движения звеньев во всех координатных плоскостях. Разработаем математическую модель шарнира для выяснения нагрузок и напряжений, возникающих в многослойной конструкции, с целью дальнейшего выяснения ресурса эксплуатации. Подобная модель может способствовать снижению энергозатрат при движениях стержневой механической системы за счет снижения сил сопротивления и рекуперации энергии.
Так как опорно-двигательный аппарат человека считается совершенным, будем в качестве основы для моделирования шарнира использовать информацию о суставе.
В экспериментальных работах в Центральном институте травматологии и ортопедии установлено, что головка тазобедренного сустава является практически идеальной сферой, за исключением шейки бедра [2]. В работах [7-9] показано, что смазка в суставе является жидкокристаллической и обеспечивает практически нулевое трение в зоне контакта и сглаживание всех несовершенств поверхности: шероховатостей, асферичности, неровностей и других отклонений поверхности от идеальной сферы. Эта смазка обеспечивает практически равномерное гидростатическое давление в суставе.
Применим к описанию поведения биологического материала модели, предложенные в работах [3-6]. Так как экзоскелет должен повторять свойства эндоскелета человека, предложим математическую модель распространения трещин в материале шарнира-сустава, пригодную для описания процессов в биологическом материале и в искусственном материале. Рассмотрим модель роста трещины в шарнире-суставе эндо- и экзоскелета человека при следующих предположениях: ходьба представляет собой процесс циклического нагружения шарнира-сустава, который приводит к постепенному подрастанию трещины (в суставе при ходьбе в фазе опоры возникают нагрузки, которые приводят к росту трещины, и есть процессы разгрузки, которые залечивают трещину, однако в среднем наблюдается рост трещины).
Сустав является системой идеальных сферических оболочек, что хорошо соответствует модели тазобедренного сустава человека. В каждом слое свойства материала одинаковы. Данное допущение является оправданным, так как в реальном суставе наблюдается подобная слоистая структура: один слой – гиалиновый хрящ, второй слой – надкостница, третий – костная ткань и т.д. В каждом из слоев свойства в среднем одинаковы. Но сфер может быть достаточно много, количество слоев в предложенной модели не ограниченно, и тем самым можно с хорошей точностью аппроксимировать свойства реального сустава.
Исследуем рост трещин в одной сферической оболочке. Рост трещин описывается одинаковыми закономерностями, различия заключаются только в значениях констант, характеризующих материал.
Рассмотрим меридиональную трещину, расположенную вдоль меридиана сферической оболочки, как показано на рис. 1. Будем считать, что при нагрузках в суставе к берегам трещины приложены равномерно распределенные усилия и моменты при симметричном распределении напряжений относительно линии трещины. То есть трещина загружена усилиями Py(x,0) = – p1 = const и изгибающими моментами My(x,0) = – p3 = const.
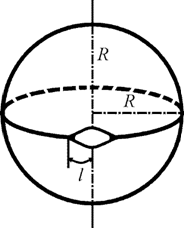
Рис. 1. Модель сферической оболочки с трещиной
Опишем процесс распространения трещины, используя коэффициенты интенсивности усилий. При таких предположениях коэффициенты интенсивности усилий и моментов около вершины меридиональной трещины в сферической оболочке в случае имеют вид [4]:
K1 = p1
(1 + 3pl2/32 + l4/(1024(3 + n))[(9p2 – 6)(3 + n) – 28n + 4(83 – 3n)ln(lg0/4) – 48(1 + 3n)ln2(lg0/4)]) + (6p3/h)(
/
)(l2/[32(3 + n)])(–7 – 12ln(lg0/4) + (pl2/[32(3 + n)])[47 – 3n – 24(5 + 3n)]ln(lg0/4)) + O(l6lnl),
K3 = – (p1h/2)[(3 + n)/
](l2/[32(3 + n)])(–1 – 7n – 4(1 + 3n)ln(lg0/4) + (pl2/1024)[(1 + 3n)/(3 + n)]{9 – n – 8(5 + 3n)ln(lg0/4)}) + p3(1 + [(1 + 3n)/(3 + n)](pl2/32) + (l4/[512(3 + n)]){–5 – 17n + [p2(1 + 3n)2/(6 + 2n)] – 2(1 + 3n)ln(lg0/4)(1 + 12ln(lg0/4))}) + O(l6lnl). (1)
Если рассматривать прямолинейную модель распространения трещины, то есть одномерный рост трещины вдоль меридиана, при нормальной нагрузке p1 = qR/2, то p3 = 0. При этом остается только один коэффициент интенсивности усилий и моментов K1. Предположение, что замкнутая оболочка нагружена равномерным внутренним давлением интенсивности q, хорошо согласуется с моделью реального сустава, в котором, как указывалось выше, имеющаяся смазка обеспечивает равномерное гидростатическое давление по всей поверхности сустава и не допускает непосредственного контакта в суставе трущихся поверхностей.
Если прорастание трещины происходит в двух направлениях, вдоль меридиана и перпендикулярно ему, то возникают сдвигающие нагрузки. При действии постоянной антисимметричной нагрузки на берегах трещины, т.е. сдвигающего усилия S(x,0) = – p2 = const и обобщенной перерезывающей силы Qy(x,0) = – p4 = const, коэффициенты интенсивности имеют вид [4]:
K2 = p2(1 + pl2/32 + (l4/1024)(p6 – 6 + 24ln(lg0/4)) + (p4l/h)[l2/32(3 + n)](1 – pl2/16) + O(l6lnl),
K4 = – [p2h/](l2/64)[(5 – n + pl2(9 – n)/32] + (p4l/2)(1 + (l4(3 – n)/[512(3 + n)])(1 + 4ln(lg0/4))) + O(l6lnl). (2)
Перейдем к рассмотрению большого количества трещин. Трещина имеет длину 2l, сфера радиус R, n – коэффициент Пуассона, l – малый параметр, характеризующий относительное расстояние между трещинами l = 2l/d = 0,5 (чаще всего, вообще 0 £ l £ 5,5), d – расстояние между центрами трещинами, lng0 = 0,5772 – постоянная Эйлера, h – толщина оболочки. Проведем численные оценки для модели головки тазобедренного сустава.
Эти коэффициенты удовлетворяют определенным условиям разрушения, после чего трещина начнет развиваться по криволинейной траектории.
q = 2arctg[(k1 – 
)/(4k2)]. (3)
Уравнение предельного равновесия при этом запишется в виде:
cos3(q/2)(k1 – 3k2tg(q/2)) = k1, (4)
где: k1 = K1/
– связан с коэффициентом сноса, k2 = K2/ – связан с коэффициентом диффузии. Если k2 ¹ 0, то трещина флуктуирует.
При ходьбе есть сдвиговые нагрузки (рис. 2). При действии на берега трещины постоянной самоуравновешенной нагрузки
sy± – itxy± = – s = const. (5)
где: sy±, txy± – компоненты тензора напряжений, знаками «+» и «–» отмечены граничные значения.
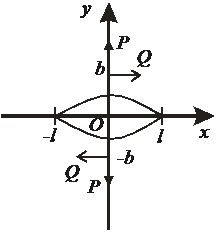
Рис. 2. Модель трещины
Коэффициенты интенсивности входят в выражение:
k1± – ik2± = s. (6)
Коэффициенты интенсивности в этом случае равны:
k1 =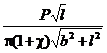 
(1 + c + 2b2/(b2 + l2)),
k1 =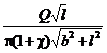 
(1 + c – 2b2/(b2 + l2)). (7)
где: P и Q – сосредоточенные нормальная и сдвигающая силы соответственно, c – упругая постоянная c = 3 – 4n – для плоской деформации, c = (3 – n)/(1 – n) – для обобщенного плоского напряженного состояния.
Проведем численные оценки коэффициентов интенсивности усилий для модели сферического сустава-шарнира модели экзоскелета.
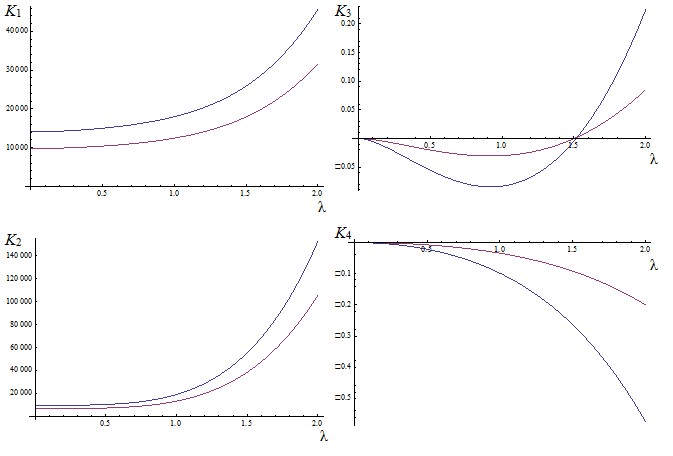
Рис. 3. Зависимость коэффициентов интенсивности усилий Ki (i = 1, …, 4) от относительного расстояния между трещинами l
На всех рисунках синяя линия соответствует хрящевой ткани головки тазобедренного сустава, коричневая – костной ткани в модели двухкомпонентной оболочки.
Зависимости для всех коэффициентов интенсивности показывают, что больше нагружается хрящевая ткань, и она имеет больший ресурс к восстановлению, т.е. залечиванию при возникновении трещин, в отличие от костной ткани. Чем больше начальное расстояние между трещинами, тем большие значения коэффициентов интенсивности возможны.
Рассмотрим теперь поведение материала сустава и костной ткани при нагрузках, соответствующих реальным при движениях в шарнирах-суставах опорно-двигательного аппарата человека. Данные нагрузки получим из результатов численного моделирования по разработанной нами методике [1]. В этом случае имеется дополнительная зависимость коэффициентов интенсивности от времени (рис. 4).
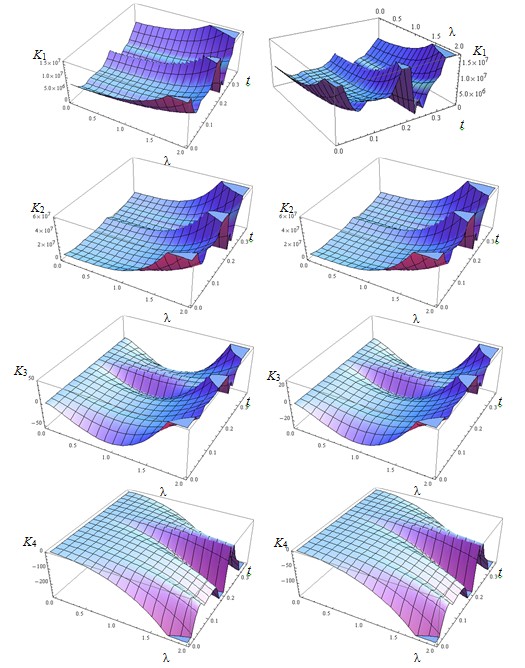
Рис. 4. Зависимость коэффициентов интенсивности усилий Ki (i = 1, …, 4) от относительного расстояния между трещинами при переменной нагрузке, изменяющейся с течением времени при ходьбе человека (слева для хрящевой ткани, справа – для кости)
По результатам расчетов видно, что зависимость от времени носит циклический характер, и сохранилось поведение в зависимости от начального расстояния в сравнении с постоянной нагрузкой.
Работа выполнена при финансовой поддержке РФФИ (грант № 13-01-97512 р_центр_а).
Рецензенты:
Денисов В.Н., д.т.н., доцент, кафедра «Высшая математика» Смоленского филиала национального исследовательского университета «МЭИ», г. Смоленск.
Мазалов М.Я., д.ф.-м.н., доцент, кафедра «Высшая математика» Смоленского филиала национального исследовательского университета «МЭИ», г. Смоленск.
Библиографическая ссылка
Борисов А.В., Гончарова И.А., Кончина Л.В., Летов Л.А. РАСПРОСТРАНЕНИЕ ТРЕЩИНЫ В ШАРНИРЕ-СУСТАВЕ ЭНДОСКЕЛЕТА // Современные проблемы науки и образования. – 2014. – № 5. ;URL: https://science-education.ru/ru/article/view?id=15068 (дата обращения: 11.09.2024).