Анализ и прогнозирование временных рядов является непрерывно развивающимся направлением теоретических и практических исследований. Тенденцией последних лет стало применение к анализу и прогнозированию временных рядов методов из нелинейной динамики, таких, в частности, как фрактальный анализ.
Применение методов анализа, основанных на фракталах, позволяет находить закономерности во временных рядах, на первый взгляд являющихся совершенно случайными [1]. Наиболее распространённым является фрактальный анализ на основании коэффициента Хёрста, получивший название RS анализ или метод нормированного размаха. В начале прошлого века гидролог Х.Е. Хёрст ( Harold Edwin Hurst) при анализе данных о разливах Нила обнаружил что 
, где Rn – скоррелированный размах, Sn – стандартное отклонение на выборке длинной n, H – коэффициент Хёрста [2].
Нормированного размаха
Коэффициент Хёрста принимает значения от 0 до 1.
Значение 0,50<H≤1,00 подразумевает персистентный временной ряд. Персистентная система проходит большее расстояние, чем случайная система. Персистентный временной ряд характеризуется эффектами долговременной памяти. Теоретически, то, что происходит сегодня, воздействует на будущее. В терминах хаотической динамики существует чувствительная зависимость от начальных условий. Такая долговременная память имеет место независимо от масштаба времени [3].
Значение 0 ≤ Н <0,50 означает антиперсистентность. Антиперсистентная система проходит меньшее расстояние, чем случайная система. Чтобы система прошла меньшее расстояние, она должна меняться чаще, чем вероятностный процесс.
Анализ Хёрста позволяет достаточно просто выявить периодические циклы и даже не периодические циклы. Для этого необходимо определить, при какой величине n в графике H-траектории, т.е. зависимости 
возникают разрывы. Или при помощи V-статистики меняет направление тренда [3].
Методика анализа довольно проста и подробно описана в [3]:
1. После подготовки данных временной ряд длины M разделяется на А смежных подпериодов длины n, так чтобы A*n=M, для каждого подпериода Ia , a = 1,2,3…A определяется среднее значение
.
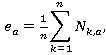
где 
– k-й элемент подпериода Ia.
2. Формируется временной ряд накопленных отклонений от среднего значения Xk,n для каждого подпериода Ia
Xk,a=
k=1,2,3,…n
3. Диапазон Rk определяется как разность максимального и минимального накопленного отклонения
,
где 1≤ k ≤ n
4. Для каждого подпериода определяется стандартное отклонение Sa
5. Каждый диапазон Ra нормализуется путём деления на Sa и определяется среднее значение R/Sдля длины n.
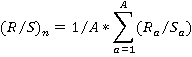
6. Процесс повторяется при увеличении n до величины М/2.
Результаты исследований
Следует отметить, что при малых n (единицы) велика погрешность метода, так что требуется довольно большая величина выборки. Так же не обязательно выполнение условия n*A=M, в этом случае - если M не кратно n последние члены ряда отбрасываются, при малых n влияние отброшенных элементов ряда будет невелико, однако при росте n погрешность будет расти. К тому же при таком алгоритме время обработки многократно возрастает.
Таким образом, для точного анализа важен не только объём выборки, но и чтобы объём этой выборки был кратен как можно большему количеству чисел.
В качестве исходных данных возьмём данные об энергопотреблении, данные фиксировались на протяжении одного года каждые тридцать минут.
Рассмотрим временной ряд среднесуточного энергопотребления за год и проанализируем его при помощи RS-анализа.
На рис. 1 представлена V-статистика и траектория показателя Хёрста среднесуточного энергопотребления, в графиках мы наблюдаем разрывы соответствующие семидневным циклам энергопотребления, что ожидаемо т.к. соответствует недельному циклу.
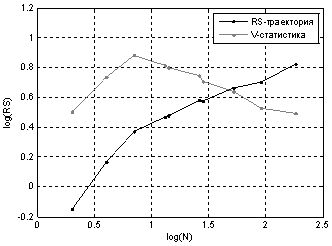
Рис. 1. - V-статистика и траектория показателя Хёрста среднесуточного энергопотребления
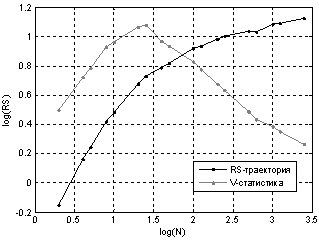
Рис. 2. – график V статистики энергопотребления за год
Коэффициент Хёрста равен H=0.95, временной ряд сильно персистентный, а значит должен достаточно легко поддаваться прогнозированию на основании данных о его предыдущих значениях.
Рассмотрим временной ряд энергопотребления за год, данные взяты с часовым интервалом.
График V статистики (см. рис. 2) показывает, что в графике показателя Хёрста присутствуют разрыв при N=24, который соответствует суточному циклу энергопотребления. Показатель Хёрста в данном случае равен H=0.91.
На рис. 3 представлена траектория показателя Хёрста, для временного ряда получасовых интервалов электропотребления. На графике V-статистики виден разрыв, соответствующий суточному циклу электропотребления. Также на обоих графиках RS-траектории присутствует разрывы, соответствующие недельному циклу.
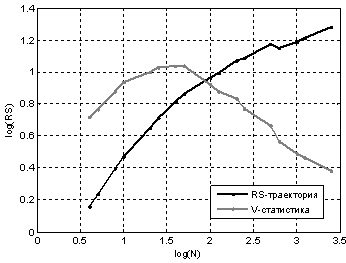
Рис. 3. - траектория показателя Хёрста для временного ряда получасовых интервалов электропотребления
Из графика H–траектории представленного на рисунке 3 видно, что показатель Хёрста H=0.8197, а значит временной ряд получасового потребления менее персистентный, чем ряд среднесуточного потребления. Таким образом, методика RS-анализа, предложенная Хёрстом, позволяет находить циклы энергопотребления, и полученные данные совпадают с ожидаемыми циклами рабочего дня, суток и недели.
Однако, RS анализ также может быть использован для оценки сложности (изрезанности) временного ряда. На основании такой оценки возможно принятия ряда мер, таких как фильтрация шума. И наоборот, применение некоторых операций, так как нормирование, может сделать анализируемый временной ряд менее персистентным, а значит, менее прогнозируемым. Покажем это на примере. Но до этого немного адаптируем алгоритм применительно к решаемой задаче.
Использование в расчёте только подвыборок кратных мощности множества приводит к снижению точности анализа и возможности потери одного из циклов. Модифицируем алгоритм анализа таким образом, чтобы рассматривались все подвыборки, объёмом не больше половины мощности множества. Если величина подвыборки не кратна величине выборки, лишние члены выборки не будут учитываться. Так как наиболее важны последние члены ряда – они оказывают влияние на будущие значения, отбрасываться будут первые члены временного ряда среднесуточного энергопотребления. При анализе временного ряда электропотребления широко применяют различные типы нормирования. Предыдущие результаты анализа были показаны для временных рядов электропотребления, нормированных по методу логарифмических разностей.
Рассмотрим, как нормирование повлияет на результаты анализа временного ряда методом нормированного размаха. На рис. 4 приведены графики RS-траектории для нормированной и ненормированной выборки среднесуточного электропотребления при анализе по всем подвыборкам.
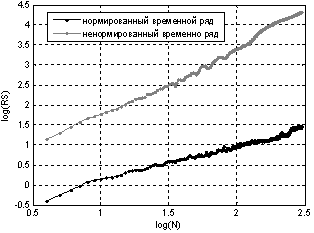
Рис. 4. - графики RS-траектории для нормированной и ненормированной выборки среднесуточного электропотребления
Показатель Хёрста не изменился, однако анализ V-статистики показал, что лучше для анализа RS-траектории после нормирования временного ряда.
Рассмотрим нормированный ряд получасового энергопотребления. На рис. 5 приведены графики RS-траектории при использовании в анализе всех выборок для нормированного и ненормированного временных рядов. На рис. 6 приведены графики V-статистики для аналогичного случая.
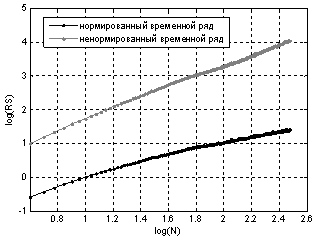
Рис. 5. - графики RS-траектории при использовании в анализе всех выборок для нормированного и ненормированного временных рядов
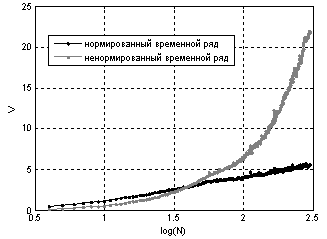
Рис. 6. графики V-статистики при использовании в анализе всех выборок для нормированного и ненормированного временных рядов
В области больших выборок (больше 300) возникают колебания графиков как V статистики, так и RS-траектории, что делает невозможным анализ наличия циклов длиной больше 300. Поэтому, можно сократить время обработки данных, ограничив максимальный объём подвыборки.
На представленных графиках присутствуют разрывы соответствующие суточному и недельному циклам, что совпадает с ожидаемыми циклами ряда энергопотребления.
Таким образом, для временных рядов среднесуточного и получасового ряда энергопотребления можно применять RS-анализ по всем подвыборкам, что позволяем добиться более точного определения длительности цикла, а также позволяет использовать достаточно большую выборку любой длины, не подбирая специально число элементов (даже если длина выборки является простым числом, анализ будет проведен). Предварительное нормирование выборки не является обязательным, но делает график Н – траектории более удобным для визуального анализа. V-статистика может быть использована только для случая нормированной выборки.
Еще один традиционный способ предварительной подготовки временного ряда к дальнейшему анализу – фильтрация шума. Применим для фильтрации вейвлет-анализ [4] и проанализируем полученный временной ряд методом нормированного размаха.
Для разложения по вейвлету используется избыточное дискретное вейвлет-преобразование (ИДВП), для реализации которого используется алгоритм «Избыточный Хаар» (алгоритм «a trous») [1]. В результате исходный временной ряд можно представить как:
, (4)
где 
– аппроксимация на уровне р, 
– коэффициенты детализации на уровнях 
соответственно. Фильтрация осуществляется путем отбрасывания последних коэффициентов детализации при восстановлении сигнала.
Величина р называется глубиной вейвлет-разложения (далее глубиной разложения) и обозначает количество уровней декомпозиции, которые используются для приближения исходного сигнала. Этот показатель определяет количество получаемых в результате разложения временных рядов и влияет на вид этих временных последовательностей. В таблице 1 приведены значения коэффициента Хёрста для различных уровней декомпозиции временного ряда получасового электропотребления при различной глубине разложения.
Таблица 1
Значения коэффициента Хёрста для различных уровней декомпозиции временного ряда
|
|
Исходный сигнал |
Аппроксимация |
Детализация 1 |
Детализация 2 |
Детализация 3 |
Детализация 4 |
Детализация 5 |
Детализация 6 |
|
Н |
0,8197 |
0,812 |
0,15 |
0,18 |
0,2 |
0,2 |
0,3 |
0,3 |
|
0,815 |
0,18 |
0,15 |
0,2 |
0,22 |
0,3 |
|
||
|
0,810 |
0,18 |
0,15 |
0,2 |
0,22 |
|
|
||
|
0,8104 |
0,15 |
0,18 |
0,2 |
|
|
|
||
|
0,813 |
0,15 |
0,18 |
|
|
|
|
Как видно из таблицы, фильтрация шума в рассматриваемом временном ряду не оказывает существенного влияния на показатель Хёрста, и даже немного понижает его. Отсюда можно сделать вывод, что данные либо не содержат шума, либо он пренебрежимо мал. Тем не менее, проведенные исследования показали, что для зашумленных сигналов фильтрация позволяет повысить коэффициент Хёрста, а значит предсказуемость временного ряда.
Что касается глубины вейвлет-разложения, то можно сказать, что увеличение уровней детализации сигнала является безрезультатным и лишь увеличивает время расчета. В [5] даны рекомендации по величине р для временных рядов в различными показателями Хёрста.
Заключение
Применение метода нормированного размаха для анализа временного ряда электропотребления выявило ожидаемые суточные и недельные циклы колебания электрической нагрузки. Предварительное нормирование выборки не является обязательным, но делает график Н – траектории более удобным для визуального анализа. V-статистика может быть использована только для случая нормированной выборки. Фильтрация шума не дает увеличения показателя Хёрста в случае, если амплитуда данного шума составляет менее 10% от амплитуды сигнала.
Работа выполнена при финансовой поддержке гранта Президента Российской Федерации №14.Z56.14.3734-МК
Рецензенты:
Поляхов Н.Д., д.т.н., профессор, профессор ФГАОУ ВО Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина), г.Санкт-Петербург;
Путов В.В., д.т.н., профессор, профессор ФГАОУ ВО Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина), г. Санкт-Петербург.
Библиографическая ссылка
Филатова Е.С., Филатов Д.М., Стоцкая А.Д. АНАЛИЗ ВРЕМЕННОГО РЯДА ЭЛЕКТРОПОТРЕБЛЕНИЯ МЕТОДОМ НОРМИРОВАННОГО РАЗМАХА // Современные проблемы науки и образования. – 2014. – № 5. ;URL: https://science-education.ru/ru/article/view?id=15063 (дата обращения: 19.04.2024).