Исследование явлений реальной действительности (наблюдение изучаемых явлений; умозрительное описание и объяснение; разработка теории, увязывающей факты) является основной целью науки. Теории могут развиваться и без обращения к наблюдениям и дать возможность предсказать, что произойдет под влиянием различных условий. Теоретические выводы могут проверяться на основе новых наблюдений. Если выводы теории согласуются с данными наблюдений, уверенность в правильности теории возрастает. Иначе ее следует признать несостоятельной. Приведенный метод исследования реальной действительности отличается цикличностью: факты, завершающие один цикл, являются началом и основой следующего цикла. Если наблюдения не подтверждают справедливость предсказаний, ведется поиск более совершенной теории. Иногда указанная схема исследований не выдерживается: теории появляются до обнаружения соответствующих явлений или теории, обоснованные наблюдениями, остаются непроверенными. Таким образом, исследование может начинаться с любого этапа.
Особое место занимает моделирование процессов и явлений. Наибольшими возможностями обладает математическое моделирование, позволяющее исследовать процессы, имеющие различное физическое содержание, но описываемые одинаковыми математическими соотношениями [1,5,7,8,9]. Заметим, что математическое моделирование успешно применяется и в самой математике (например, решения, полученные численными методами, являются моделями истинных решений – моделями реальных объектов).
Сложность и многообразие процессов функционирования реальных систем не позволяют получить абсолютно адекватные математические модели. Математическая модель, описывающая формализованный процесс функционирования системы, в состоянии охватить только основные, характерные закономерности. Надо помнить, что нет возможностей указать формальные правила для выбора характеристик состояний и параметров исследуемых реальных систем. Исследователь вынужден руководствоваться лишь собственной интуицией, опирающейся на постановку прикладной задачи и понимание природы процессов функционирования системы [2,4,10].
Анализ каждой сложной системы – это уникальная проблема, требующая не только разносторонней культуры, но и изобретательства и таланта. В системном анализе сочетаются экспериментальное, эвристическое и строгое математическое начала. В настоящее время системный анализ, как синтетическая дисциплина, включает целый ряд разделов, носящих характер самостоятельных научных дисциплин [3,11, 12].
Основная проблема прикладного математического анализа состоит в определении общей закономерности на основе отдельных частных наблюдений. Это относится и к задачам строительного материаловедения.
Как правило, общая схема взаимодействия переменных в исследуемой системе имеет вид приводимой на рисунке.
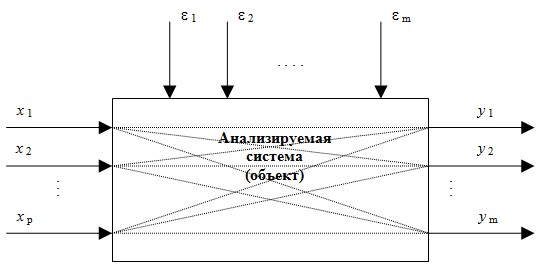
Рис. Взаимодействие переменных в системе
Входные переменные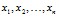 
(независимые, объясняющие переменные; факторы, предикторы (предсказатели)) описывают условия функционирования системы. Некоторые из них поддаются регулированию или частичному управлению. Поведение, результат, эффективность функционирования системы характеризуются выходными переменными 
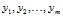(отклики; результирующие, объясняемые переменные). Случайные латентные переменные 
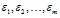(не поддаются непосредственному измерению) отражают влияние на 
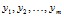соответственно неучтённых на входе факторов (случайные ошибки измерения анализируемых показателей; «остатки»). Так, например, при зимнем бетонировании применяется электропроводный бетон, прочность которого зависит от его состава. Здесь факторами будут процентное содержание портландцемента –
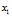, песка – 
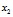, графита – 
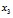, воды – 
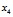соответственно. В качестве 
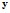будет прочность электропроводного бетона. Влияние не учитываемых переменных войдёт в состав 
.
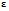Основная задача состоит в построении функции
= 
,
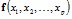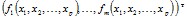в некотором принятом смысле позволяющей наилучшим образом восстанавливать значения переменной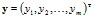 
по 
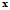
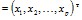, т – символ транспонирования.
План исследования начинается с установления конечной прикладной цели. Далее производятся выбор структуры математической модели, интерпретация получаемых результатов. В строительном материаловедении основными целями исследований обычно являются:
-
установление самого факта наличия (или отсутствия) статистически значимой связи между переменным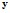и
и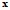 
;
-
прогноз (восстановление)
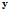по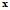 
(здесь интересуют лишь значения 
(
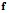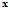), но не структура самой функции);
-
выявление причинных связей между
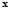и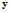 
, частичное управление 
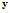путём регулирования 
.
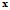Среди компонент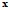 
и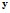 
различают:
-
количественные (например, процентное содержание входящих в материал компонент);
-
порядковые или ординальные (позволяют упорядочивать анализируемые объекты по степени проявления в них изучаемого свойства; например, уровень образования работника, разряд рабочего и т.д.);
-
классификационные или номинальные (позволяют разбивать объекты на не поддающиеся упорядочиванию однородные классы; например, способы обработки железобетонных изделий, наличие конкурирующих добавок или заполнителей и др., профессия работника, отрасль промышленности, мотив миграции семьи и т.д.).
Решение этих задач позволяет определить физический смысл статистических связей (например, исследования в области промышленности строительных материалов по определению зависимостей изучаемых свойств материалов от ряда факторов [1,13]).
Отметим, не существует стандартных приёмов и методов для правильного определения структуры модели (общий вид функции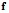 
(
) ).
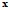Укажем основные используемые этапы статистического исследования зависимостей.
1. Постановочный. Здесь каждому элементарному объекту исследования ставится в соответствие набор анализируемых показателей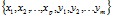 
. Определяются конечные цели исследования, тип исследуемых зависимостей, форма и степень точности статистических выводов.
2. Информационный этап состоит в сборе по результатам n измерений статистической информации вида
.
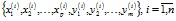3. Корреляционный анализ устанавливает наличие или отсутствие какой-либо связи между исследуемыми переменными, определяется структура связей и их теснота.
4. Определение класса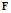 
допустимых решений. На этом этапе определяется вид, структура искомой связи между 
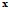и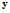 
(семейство функций 
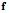). Часто описание даётся в форме параметрического семейства функций 
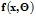(параметризация модели).
5. Вычисление оценок параметров, входящих в исследуемое уравнение статистической связи.
Если класс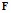 
задаётся в виде параметрического семейства функций
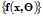, то задача сводится к подбору (статистическому оцениванию) значений Θ из условий экстремума некоторого функционала (например, метода наименьших квадратов).
6. Анализ точности полученных уравнений связи.
Часть исследований, объединяющая этапы 4, 5, 6, является основной задачей регрессионного анализа.
Разработка методологических принципов синтеза строительных материалов специального назначения на основе моделирования процессов формирования их структуры и свойств фактически сводится к решению ряда взаимосвязанных задач:
- в соответствии с введенной иерархией критериев и выделенными комплексами решаемых частных задач строится иерархическая структура системы (материала) с оценками её элементов (служит основой перспективного планирования всего комплекса разработок и отдельных систем);
- определяются методологические принципы синтеза строительных материалов (например, для разработки радиационно-защитных материалов с регулируемыми структурой и свойствами) с использованием классической теории управления, методов системного анализа в сочетании с экспериментальными, эвристическими методами материаловедения;
- осуществляется идентификация кинетических процессов формирования структуры и основных физико-механических характеристик материала с оценкой точности их математического моделирования;
- разрабатывается обобщенная модель кинетических процессов;
- определяются связи между параметрами структуры и кинетических процессов;
- строятся функционалы качества;
- анализируются возможности и выбор метода преодоления неопределенностей целей;
- предлагается единая концепция синтеза строительных материалов со специальными свойствами, допускающая использование итеративного способа.
Целесообразно строительный материал рассматривать как сложную систему, что в полной мере позволяет использовать системный подход при моделировании структуры и свойств композиционных материалов специального назначения. Появляется возможность на основе когнитивного моделирования [6] разработать иерархическую структуру качества и соответствующую ей иерархическую структуру материала специального назначения, а далее, с применением методов идентификации и на основе специально разработанного функционала, производить многокритериальный синтез строительного материала. Использование такого подхода позволило создать сверхтяжелые бетоны для защиты от радиации, а также химически-стойкие материалы, представляющие интерес на международном рынке защитных материалов и технологии их производств.
Рецензенты:
Береговой В.А., д.т.н., профессор кафедры «Технология строительных материалов и деревообработки» Пензенского государственного университета архитектуры и строительства, г. Пенза;
Логанина В.И., д.т.н., профессор, зав. кафедрой «Управление качеством и технологии строительного производства» Пензенского государственного университета архитектуры и строительства, г. Пенза.
Библиографическая ссылка
Гарькина И.А., Данилов А.М., Петренко В.О. ИЗ ОПЫТА РАЗРАБОТКИ МАТЕРИАЛОВ СПЕЦИАЛЬНОГО НАЗНАЧЕНИЯ // Современные проблемы науки и образования. – 2014. – № 5. ;URL: https://science-education.ru/ru/article/view?id=15043 (дата обращения: 20.04.2024).