Одной из основных задач образования является формирование активной творческой личности, что, в свою очередь, требует развития мыслительной деятельности, совершенствования практических умений и навыков и т.д. [12, 13, 9]. В ряду этих актуальных проблем важное место занимает проблема формирования и развития пространственных представлений обучающихся. Несмотря на столь большую роль, которую играют пространственные представления, сформированность их у выпускников школ находится на остаточно низком уровне [10, 4].
При исследовании проблемы формирования и развития пространственных представлений обучающихся возникает вопрос о существовании специфики данного понятия в методике обучения математике. В процессе изучения математики, в частности, геометрии, происходит формирование представлений о геометрических конфигурациях, о взаимном расположении их элементов и отношениях между ними, а затем осуществляется дальнейшее оперирование созданными представлениями в ходе решения задач.
Особенность таких представлений состоит в том, что сами пространственные конфигурации в геометрии являются не объектами реального мира, а мыслительными образами, полученными в результате абстрагирования от этих объектов и содержащими в себе их существенные свойства и признаки. Для формирования таких представлений, уже на первых этапах необходима опора на определенные знания о рассматриваемых геометрических объектах, то есть сразу же начинает работать не только пространственный (создание образа), но и логический (выявление существенных признаков) компонент мышления. Пространственные представления по отношению к мышлению являются исходной базой, условием развития, но и формирование представлений требует предварительного овладения понятиями и фактами. Можно сказать, что процесс формирования пространственных представлений о геометрических объектах проходит на основе знаний о них [7].
Таким образом, содержание пространственных представлений в теории и методике обучения математике следует рассматривать не просто как образ отраженного объекта или явления, оно включает в себя также и знания, доступные обучаемым данного возраста, связанные с этим объектом и извлеченные в процессе его восприятия. Это скорее результат визуального мышления, сочетающего в себе взаимосвязанные пространственный и логический компоненты мышления.
Итак, под пространственным представлением, формируемым в процессе обучения геометрии, будем понимать обобщенный образ геометрического объекта, складывающийся в результате переработки (анализа) информации о нем, поступающей через органы чувств. Другими словами, пространственное представление геометрического объекта является результатом деятельности визуального мышления, связанного с этим объектом.
В исследовании Н.А. Резник [11] рассмотрена структура визуальной деятельности учащихся в процессе изучения математики, но автор не соотносит ее с формированием пространственных представлений школьников. Логика нашего исследования требует рассмотрения основных этапов визуальной деятельности в процессе формирования пространственных представлений обучаемых и выделения основных видов этой деятельности при обучении математике.
Первым шагом на любом этапе познания, в том числе и при формировании представлений, является восприятие, «живое созерцание» определенной визуальной информации, например, чертежа, схемы, модели, рисунка и т.п. Для того чтобы сделать его действенным, необходимо не просто смотреть на предлагаемые для восприятия зрительные образы, а видеть заложенную в них информацию, то есть осуществлять анализ визуальной информации.
Анализ визуальной информации начинается с осознания общей структуры информационного сообщения, заложенного в данном зрительном образе (модели, рисунке, чертеже, схеме и др.) и выделения его элементов. Учебная математическая информация, задаваемая наглядным образом, довольно четко подразделяется на элементы. Например, при изображении пространственных или плоских геометрических конфигураций, в одних случаях к элементам можно отнести сами эти фигуры, в других – выделенные на чертеже их составляющие (высоты, углы, стороны, вершины и др.). Таким образом, происходит расчленение, зрительный анализ информации, в котором важную роль играет опознание отдельных ее фрагментов (узнавание), отождествление одинаковых, сходных по форме или по смыслу ее элементов. Система связей выделенных элементов, образующих целое – исходную информацию – будет составлять структуру данной визуальной информации. Осознание структуры исходной визуальной информации заключается в определении связей между ее элементами.
В ходе активного зрительного восприятия визуальной информации обучаемый отождествляет отдельные ее фрагменты с известными ему достаточно простыми объектами и понятиями, которые можно назвать стандартами. Под визуальными стандартами будем понимать такую визуальную интерпретацию математического понятия (свойства), которая наиболее полно и точно отображает его словесное определение. При этом акцент на образ способствует установлению немедленной зрительной ассоциации с абстрактным понятием, которое предшествует словесному описанию.
Распознавание стандартной ситуации, стандарта может происходить как по постановке задачи (применить признак параллельности для построения сечения куба), так и неявно, в процессе выделения знакомого представления в новых условиях (стороны треугольника – отрезки, вершины – точки), уяснения частного вида более общего знакомого понятия (треугольник – равносторонний треугольник).
Таким образом, в посильном для изучения материале обучаемый находит некоторые известные ему объекты, материализованные, например, в виде элементов чертежа, схемы, графика, модели; выделяет их, дифференцирует по степени сходства, определяет известный ему структурный стандарт по отношению ко всей представленной визуальной информации. Получение начальных, явным способом предлагаемых, данных информации приводит к вычленению признаков геометрического объекта, которые являются основой для формирования его первичного образа [8].
Далее обучаемый приступает к уточнению и детализации исходной визуальной информации, сравнивает ее с некоторым обобщенным образом (стандартом, эталоном). Вследствие проделанной работы происходит получение (выявление) новой, дополнительной информации, при этом еще раз уточняются и проверяются знания об объекте, оценивается его отличие от стандарта. Таким образом, в памяти обучаемого происходит окончательное закрепление – образование содержательных образов (пространственных представлений).
Вся деятельность визуального мышления при работе с наглядным материалом направлена на формирование обобщенных пространственных представлений, несущих в себе определенную содержательную информацию об объекте. Созданные пространственные представления не должны быть чем-то застывшим, их внедрение в учебный процесс предполагает не только последовательное восстановление созданных представлений (воспроизведение), но и, при необходимости, их расчленение, сборку отдельных элементов в единое целое – новое образование (оперирование образами геометрических объектов и конструирование образов новых геометрических конфигураций), включение пространственных представлений в новые связи, что будет способствовать формированию обобщенных пространственных представлений, близких к понятиям.
Развитие сформированных представлений, обогащение их содержания осуществляется в процессе решения задач, требующих оперирования ранее созданными пространственными представлениями, происходит включение пространственных представлений в новые связи, помещение их в новые условия, определяемые условием задачи. В ходе визуального анализа формируется тактика переработки этой информации в соответствии с поставленными задачами, оперирование созданными пространственными представлениями в процессе их решения, происходит мысленное составление плана работы. По своим целям и учебным возможностям этот этап можно отнести к поисковой деятельности [1, 3]. Обучаемый определяет порядок действий, пытается в уме выполнить некоторые из знакомых ему операций, рассмотреть возможные варианты решения задачи, прогнозировать результат. Каждый геометрический образ имеет определенную структуру, позволяющую зрительно выделить и проанализировать его логический «фундамент». Подобная структура есть некоторая визуальная модель информационного сообщения, которую можно использовать в решении поставленной задачи [6].
В процессе решения задач, ориентированных на развитие пространственных представлений, представления приобретают новые формы, направляющие мыслительную деятельность обучаемого так, что из исходных данных он может извлечь ориентиры и подсказки, построить догадку, приводящую к получению правильного ответа. В ходе поиска решения задачи осуществляется порождение новых пространственных представлений, несущих определенную визуально-логическую нагрузку и делающих видимым значение исходного объекта или его свойства. Отправными моментами и точками опоры такого процесса является запас готовых, сформированных у обучаемого пространственных представлений, их элементы и структура, визуально обозримые связи между ними.
Процесс решения таких задач включает: а) перевод текста в визуальную информацию; б) анализ визуальной информации, распознавание стандартов (сформированных ранее пространственных представлений); в) включение их в новые условия, определяемые задачей; г) выявление ориентиров и подсказок, составление мысленного плана решения; д) решение задачи, получение ответа.
Рассмотрим, например, задачу на построение сечения куба плоскостью, проходящей через три заданные точки (М![]() А1Д1, Р
А1Д1, Р![]() В1С1, К
В1С1, К![]() СД).
СД).
а) Перевод текста в визуальную информацию (см. рис. 1):
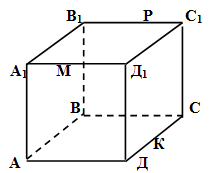
Рис. 1
б) Анализ визуальной информации: выделяются элементы данной структуры (куба) – ребра, грани куба, заданные точки, принадлежащие ребрам. Стандарт – представление о кубе, включающее знания о нем.
в) Включение стандарта в новые связи, определенные задачей: М![]() А1Д1, Р
А1Д1, Р![]() В1С1, К
В1С1, К![]() СД.
СД.
г) Определение подсказок и ориентиров, составление плана решения:
- точки М и Р принадлежат плоскости одной грани, следовательно, через них можно провести прямую МР;
- противоположные грани куба параллельны, следовательно, через точку К можно провести прямую КЕ, параллельную МР;
- Е – точка пересечения прямых КЕ и АД, Е и М принадлежат одной грани, следовательно, можно провести прямую МЕ;
- противоположные грани куба параллельны, следовательно, через точку Р можно провести прямую РО, параллельную МЕ;
- О – точка пересечения прямых РО и СС1, О и К принадлежат одной грани, следовательно, можно провести прямую ОК;
- МРОКЕ – искомое сечение куба.
д) Задача решается фактически с помощью чертежных инструментов (см. рис. 2).
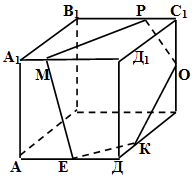
Рис. 2
Обобщая все сказанное выше, можно выделить основные этапы (определить последовательность) формирования и развития пространственных представлений в процессе визуальной деятельности:
1. Восприятие и анализ визуальной информации.
2. Распознавание стандартов.
3. Получение новой (дополнительной) информации (первичный образ).
4. Включение формируемого пространственного представления в новые связи (обобщенный образ).
5. Оперирование пространственными представлениями в новых условиях, определяемых задачей (развитие пространственных представлений) [5].
Итак, пространственные представления, создаваемые в процессе обучения геометрии, рассматриваются нами как результат визуального мышления, связанного с объектом восприятия, представление о котором формируется. Анализ визуальной деятельности позволил выявить этапы формирования и развития пространственных представлений при обучении математике и определить основные ее виды, лежащие в основе данного процесса: узнавание, воспроизведение, оперирование пространственными представлениями, конструирование новых пространственных представлений.
Рецензенты:
Фролов И.В., д.п.н., профессор, заведующий кафедрой физики, теории и методики обучения физике Арзамасского филиала «Нижегородский государственный университет им. Н.И. Лобачевского», г. Арзамас;
Санина Е.И., д.п.н., профессор кафедры общих математических и естественнонаучных дисциплин ГБОУ ВПО МО «Академия социального управления», г. Москва.
Библиографическая ссылка
Маклаева Э.В. ЭТАПЫ ФОРМИРОВАНИЯ И РАЗВИТИЯ ПРОСТРАНСТВЕННЫХ ПРЕДСТАВЛЕНИЙ ОБУЧАЮЩИХСЯ В ПРОЦЕССЕ ОБУЧЕНИЯ МАТЕМАТИКЕ // Современные проблемы науки и образования. 2014. № 5. ;URL: https://science-education.ru/ru/article/view?id=14938 (дата обращения: 09.02.2026).



