Современная тенденция развития транспортного строительства в России направлена на использование в производстве материалов техногенного сырья, в частности промышленных отходов. Рециклинг отходов способствует защите окружающей среды от загрязнения, решает проблему утилизации опасных отходов и обеспечивает промышленность дешевым сырьём. Наиболее перспективными материалами на сегодняшний день являются композиционные материалы (КМ) на основе древесных и промышленных отходов. В России использование КМ в сфере транспортного строительства принимает промышленные масштабы. Расширение области применения и создание новых КМ обуславливает предъявление соответствующих требований по физико-механическим характеристикам, в частности по прочностным параметрам, что приводит к необходимости разработки новых методов и средств математического моделирования свойств композитов [2].
В настоящее время в достаточной мере проработаны положения общей теории математического моделирования, созданы теоретические основы общей методологии моделирования КМ. Однако существующие методы расчета характеристик элементов транспортного строительства, как правило, основаны на предположениях о характере распределения микронапряжений в матрице и волокнах, что позволяет получить относительно простые аналитические соотношения напряженного и деформированного состояний композитов. Такие методы часто не обеспечивают необходимой точности расчетов.
Таким образом, на данный момент весьма актуальным является создание новых научных основ технологии получения эффективных и экологически безопасных композиционных материалов с использованием отходов лесной, нефтехимической, полиэтиленовой и других отраслей промышленности, что позволит создать новые элементы и изделия, используемые в транспортном строительстве [4].
Весьма актуальным является исследование физических свойств природных полимеров, к которым относится древесина. Композиционный материал чаще всего работает в условиях сложного напряженного и деформированного состояний (НДС). Это утверждение полностью относится и к изделиям транспортного строительства, таким как шпалы, плиты, блоки и т.д., состоящим, в основном, из композита и заполнителя в виде древесины [5]. Однако существующие в настоящее время приборы для механических испытаний композиционного материала реализуют в испытываемых образцах, как правило, простое НДС – одноосное растяжение-сжатие, простой или чистый сдвиг, изгиб.
Обратим внимание на то, что нормальные напряжения являются внешней удельной силой, которая приложена к образцу определенной формы и меняет внутренние напряжения, это условные напряжения, или условный эквивалент внутренних напряжений, т.к. обязательным условием являются форма образца и определенный порядок проведения испытаний. Что такое внутренние напряжения, как и где они возникают, можно понять, только разобравшись в физике процесса сопротивляемости материала деформированию (понятие элементарного объема из механики разрушения, в котором и происходят характерные изменения материала при его деформировании).
Мы можем измерить продольные и поперечные деформации вдоль и поперек оси приложенной силы, которые определяются как алгебраические суммы проекций векторов внутренних физических деформаций.
Это несоответствие усложняет задачу прогнозирования механических свойств композита, работающих в различных изделиях специального назначения в реальных условиях эксплуатации. На основе экспериментов, проведенных в простом НДС, с помощью чисто расчетных методов трудно с хорошей точностью рассчитать свойства композита в сложном НДС.
В настоящее время механические свойства композиционных материалов для шпал, плит и др. задаются при проектировании в большинстве случаев всего двумя характеристиками (модулями Юнга и всестороннего сжатия) [6]. Сколько и какие характеристики надо включать в расчетный метод проектирования композита, какими зависимостями описывать механические свойства – такие вопросы в настоящее время исследованы недостаточно. Если мы не будем изучать этот вопрос - не поймем, как правильно включить свойства материалов в расчетные методы, и попытки приблизить результат расчета к реальности не приведут к требуемому повышению качества изделия [3].
Появление высокопроизводительной и недорогой вычислительной техники, а также программное обеспечение к ней значительно облегчает многие трудоемкие математические расчеты.
Рассмотрим спроектированные составы древесного полимерпесчаного композиционного материала (ДППКМ) для изделий транспортного строительства, расчет которых был основан на обеспечении прочности и жесткости при различных видах механических нагрузок – кратковременных, длительно действующих и динамических, остались мало изученными и неучтенными в нем целый ряд физических воздействий – усадка, набухание под действием воды и их сочетания. Сложным и совершенно не изученным являются напряженное и деформированное состояния в окрестности произвольной точки объема элемента конструкции из древесного композита, возникающие в нем под действием вышеназванных факторов.
В связи с изложенным в качестве одной из основных задач исследований явился анализ напряженного и деформированного состояний в кубе из ДППКМ под действием усадки и набухания при всестороннем увлажнении и, в особенности, стесненного набухания древесного заполнителя, в который диффузионно при адсорбции из полимера проникает вода.
За объект исследований был принят куб из ДППКМ, представляющий собой кубик из древесины сосны (рис. 1), выпиленный из ее ствола в соответствии с тремя взаимно перпендикулярными плоскостями упругой симметрии и заключенный в полимерную оболочку из полимерпесчаного КМ (рис. 2).
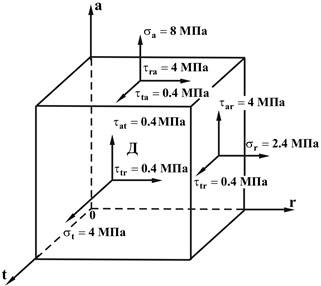
Рис. 1. Объемное напряженное состояние у произвольной точки «О» в объеме кубика из древесины сосны под действием усадочных напряжений в полимерной оболочке из ППКМ и давления набухания.
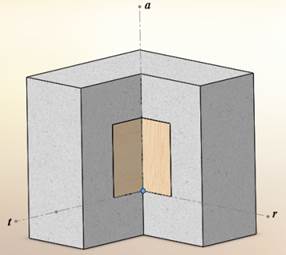
Рис. 2. Куб из древесины сосны, помещенный в полимерную оболочку из ППКМ.
Это позволило, ввиду малого объема кубика, пренебречь кривизной годичных слоев и приписать древесине свойства ортогональной анизотропии, т.е. считать ее ортотропным телом, имеющим три взаимно перпендикулярные плоскости упругой симметрии. Две из них продольные (по отношению к годичным слоям) – это радиальная и тангенциальная плоскости, третья – перпендикулярная к направлению волокон [1].
Направления, нормальные к плоскостям упругой симметрии, называют главными направлениями упругости. Их совмещают с направлениями координатных осей и обозначают соответственно: a – вдоль волокон, r – радиальное направление поперек волокон, t – тангенциальное направление поперек волокон.
Таким образом, модель объекта испытаний выглядит следующим образом (рис. 3).

Рис. 3. Модель объекта исследований.
Для определения главных напряжений, положения главных площадок, а также главных упругих относительных деформаций и их направления, помимо нормальных напряжений, изображенных на рисунке 1, использовали (при Т=20 °С и W=12%) следующее.
Упругие относительные деформации кубика из древесины, растяжение (рис. 1):
![]()
![]()
![]()
Модули сдвига: Gra=0,114×104 МПа, Gtr=0,005×104 МПа, Gta=0,071×104 МПа.
Положительные по своему направлению касательные напряжения:
|τar|=|τra| = 4 МПа; |τrt|=|τtr| = 0,4 МПа; |τat| = |τta| = 0,4 МПа.
В результате произведен анализ напряженного состояния в кубике древесины сосны (рис. 1), определены компоненты тензора напряжений:
σt = 0,4 МПа, σr = 2,4 МПа, σа = 8,0 МПа,
|τar| = |τra| = 4,0 МПа; |τrt| = |τtr| = 0,4 МПа; |τat| = |τta| = 0,4 МПа;
инварианты: I1 = σt+σr+σа; I1 = 14,4, I2 = σrσt+σrσа+σtσа-τ2tr-τ2ar-τ2at; I2 = =44,48, I3 = σrσtσа+σrσа+σtσа-τ2trσа-τ2arσt-τ2atσr+2τtrτarτat; I3 = 12,416.
Произведен поиск корней полинома (ri) с использованием определителя «М», т.е. найдены значения главных напряжений (учитывая, что σ1>σ2>σ3, МПа):
σ1 =10,37; σ2 = 3,97; σ3 =0,311.
Произведен анализ деформированного состояния, найдены компоненты тензора деформаций: ![]() εt=0,008; εr=0,004; εa=0,00065; γra=τra/Gra; γtr=τtr/Gtr; γta=τta/Gta; γra=3,509×10–3; γtr=8,0×10–3; γta=5,634×10–4.
εt=0,008; εr=0,004; εa=0,00065; γra=τra/Gra; γtr=τtr/Gtr; γta=τta/Gta; γra=3,509×10–3; γtr=8,0×10–3; γta=5,634×10–4.
Главные деформации для осей а-t: ![]() ;
;
![]() .
.
Главные деформации для осей t–r:
![]() ;.
;.
![]()
Главные деформации для осей а–r:
![]() ;
;
![]() .
.
Проведенные расчеты показали, что наибольшее главное напряжение, равное σ1=10,37 МПа, меньше, чем предел прочности ППКМ при растяжении (![]() =19,87 МПа), но несколько выше предела пропорциональности (
=19,87 МПа), но несколько выше предела пропорциональности (![]() =9,69 МПа), но наибольшую опасность представляет собой величина главной относительной деформации по направлению между осями t–r, равная 10×10-3, которая превышает даже максимальные относительные деформации при трещинообразовании, равные 6,6×10-3, т.е. действие воды ухудшило напряженное и деформированное состояния внутри куба из ДППКМ.
=9,69 МПа), но наибольшую опасность представляет собой величина главной относительной деформации по направлению между осями t–r, равная 10×10-3, которая превышает даже максимальные относительные деформации при трещинообразовании, равные 6,6×10-3, т.е. действие воды ухудшило напряженное и деформированное состояния внутри куба из ДППКМ.
По результатам вычислений были созданы компьютерные имитационные модели возникающих напряжений и деформаций [5], возникающие по направлению вдоль волокон (ось а), по радиальному направлению поперек волокон (ось r), по тангенциальному направлению поперек волокон (ось t). На рисунке 4 представлено напряженное и деформированное состояния объекта исследования.
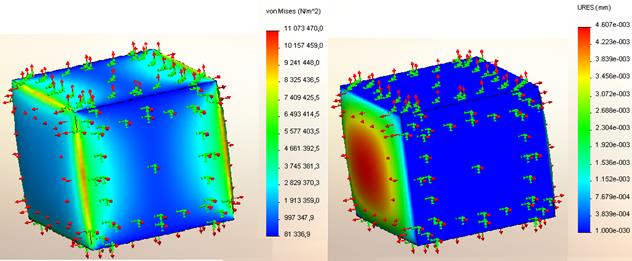
Рис. 4. Наибольшие напряжения и деформации, возникающие в кубике из древесины сосны по тангенциальному направлению поперек волокон (напряженное и деформированное состояния).
Анализируя построенные модели, можно сделать вывод, что в результате набухания древесного заполнителя, в который при адсорбции из полимера проникает вода, максимальные напряжения возникают на кромках куба. Наибольшие напряжения и деформации возникают в тангенциальном направлении.
Исходя из анализа вычислений и полученных компьютерных имитационных моделей, была получена общая модель объекта исследования, из которой видно, что напряжения, возникающие вследствие разбухания древесного наполнителя, воздействуют на полимерную оболочку из ППКМ, а полимерная оболочка на наполнитель. Таким образом, максимальное напряжение, возникающее при таком взаимодействии, составляет 15,19 МПа, а деформация не превышает 0,0263 мм.
Выводы
Таким образом, получены с применением ЭВМ аналитические выражения, позволяющие подсчитывать главные напряжения и относительные деформации, учитывающие прочностные и упругие характеристики двух основных компонентов ДППКМ – полимерной матрицы и древесины, что позволило определить основную причину появления микро- и макротрещин, а затем разрушение структуры этого материала – это низкую деформативность отвержденного полимерного связующего. Предложенный метод соответствует современным требованиям компьютерного материаловедения.
Рецензенты:
Астанин В.К., д.т.н., профессор, заведующий кафедрой технического сервиса и технологии машиностроения ФГБОУ ВПО «Воронежский государственный аграрный университет имени императора Петра I», г. Воронеж.
Мануковский А.Ю., д.т.н., доцент, профессор кафедры промышленного транспорта, строительства и геодезии ФГБОУ ВПО «Воронежская государственная лесотехническая академия», г. Воронеж.
Библиографическая ссылка
Стородубцева Т.Н., Аксомитный А.А. МОДЕЛИРОВАНИЕ СЛОЖНОГО НАПРЯЖЕННОГО СОСТОЯНИЯ ДРЕВЕСИНЫ И ПОЛИМЕРНОЙ МАТРИЦЫ // Современные проблемы науки и образования. 2014. № 5. ;URL: https://science-education.ru/ru/article/view?id=14585 (дата обращения: 01.03.2026).



