На сегодняшний день задача инкассации является одной из наиболее актуальных из класса задач маршрутизации, поскольку каждая компания, предоставляющая подобные финансовые услуги, нуждается в оптимизации своих затрат.
Существует множество вариаций различных ограничений для данного типа задач, например, ограничения по времени заезда, по количеству депо и по виду транспортных средств, и применяются они как совместно, так и по отдельности [6].
Рассмотрим классическую задачу с дополнительными ограничениями: по времени и количеству человек, которое необходимо для обслуживания того или иного объекта. Для данной задачи математическая модель примет следующий вид:
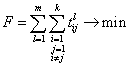(1)
, 
,
(2)
(3)
(4)
(5)
Целевая функция (1) минимизирует время обслуживания объекта, здесь 
– время, затрачиваемое на преодоление пути от объекта 
до объекта 
; 
– индекс, отвечающий за обход по маршрутам; 
– количество маршрутов. Ограничение (2) означает, что каждый объект обслуживается один раз, а также может принадлежать только одному лепестку. Ограничение (3) подразумевает под собой максимальный объем груза, который вмещается в транспортное средство, где 
– грузоподъемность автомобиля; 
– вес точки, который необходимо погрузить в машину; 
– вес, который необходимо выгрузить. (4) – ограничение на время закрытия объекта: 
– время закрытия объекта, 
– время обслуживания точки, 
– время выезда -ой бригады из депо. Ограничение (5) говорит о том, что количество обслуживающих рабочих, приехавших на объект, не должно быть меньше, чем необходимо данному объекту.
Данная задача относится к NP-трудных задач. Существует несколько методов решения таких задач, а именно – точные, эвристические и метаэвристические методы [4]. Точные методы основываются на полном переборе всех возможных решений, что, в свою очередь, делает их неэффективными, поскольку длительность поиска решений занимает большой промежуток времени [2]. Минус точных методов учитывается в эвристических. Они производят относительно ограниченный поиск решений, которые дает довольно хорошее решение за приемлемое время, но решение является приблизительным [2]. Самыми оптимальными методами, которые находят довольно быстро и хорошее решение, являются метаэвристические методы. Но в данных методах также имеется минус –есть параметр, который напрямую влияет на результат, исходя из входных данных [3].
Метаэвристические методы представляют собой двухэтапные алгоритмы[7]. Идея данных методов заключается в следующем: на первом этапе находится приближенное решение, на втором происходит его улучшение. При реализации второго этапа сложностей не возникает, поскольку улучшающие методы хорошо изучены, к ним можно отнести метод отжига, генетический алгоритм и муравьиный алгоритм и др. Но была обнаружена проблема нахождения метода, который на первом этапе получал бы маршрут наиболее близкий к оптимальному, т.е. с небольшой погрешностью.
Задача в данной постановке подробно разбирается в работе [1]. В ней рассмотрен подробно алгоритм решения выше поставленной задачи, а также приведена блок-схема изложенного метода.
В данной работе представлены доработанные процедуры по формированию маршрута: Sort By Last Time и Add Point Without Waiting. Ниже приведена блок-схема новой функции Add Point, которая включает в себя вышеуказанные процедуры (рис.1).
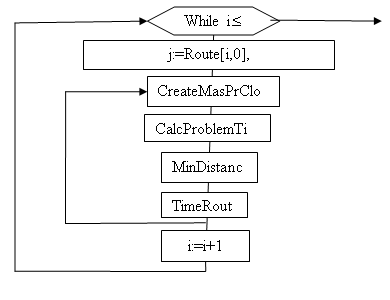
Рис. 1. Блок-схема процедуры Add Point
Алгоритм, заложенный в основу данной процедуры, является модификацией жадного метода, т.е. в маршрут добавляется точка с минимальным расстоянием при условии, что она удовлетворяет всем ограничениям, наложенным на время.
В блоке Create Mas Pr Close формируется массив, в котором точки расположены в порядке возрастания времени закрытия объектов при помощи формулы: 
, где 
– последняя включенная в маршрут. После сформирования массива берется первый его элемент 
и относительно него проводится процедура Calc Problem Time, которая показывает, успеет ли бригада обслужить другие объекты, если заедет в объект. В основе данной процедуры лежит следующая формула: 
. Если 
для всех точек принимает значение больше нуля, то это означает, что бригада успевает во все точки, с учетом заезда в объект.
В Min Distance формируется массив точек, которые находятся на минимальном расстоянии от точки . Именно в данной процедуре заключается идея «жадного алгоритма» [5], т.е. бригада заезжает в ближние точки, в которые успевает. После того, как выбирается какой-либо объект 
из массива Min Distance, проверяется условие на включение в маршрут данной точки по формуле: 
, где 
. Если данная величина больше нуля, то ждать открытия объекта не нужно, и в данный объект можно заехать, прежде чем ехать в первый закрывающийся. После того, как объект включается в маршрут, необходимо поменять время бригады в пути.
Алгоритм выполняется до тех пор, пока все объекты не будут включены в маршрут. И данный набор процедур выполняется для всех лепестков.
Для проверки алгоритма был разработан программный продукт. Данные в программу скачиваются из файла Microsoft Excel и хранятся в ней в виде динамических массивов. Это вызывает ряд неудобств, связанных с обращением к элементам массива, но делает программу более универсальной и оптимальной по количеству занимаемой памяти. Для хранения нескольких параметров, относящихся к одной точке, в ячейках массива используют записи с несколькими полями. Такой тип хранения переменных выбран в связи с тем, что, обращаясь к определенной переменной, можно быть уверенным в соответствии данных выбранной точке.
В работе берется 81 точка с учетом депо, то есть 80 объектов, которые необходимо обслужить. Количество человек, обслуживающих каждую из точек, составляет 2 или 3 человека. Время выезда бригад из депо одинаково, также как и вместимость транспортных средств. Заданы различные веса для каждой точки, различное время закрытия и открытия, а также время обслуживания.
После запуска программы получено 6 лепестков. Рассмотрим более подробно 4 лепесток. На рис.2 представлен маршрут движения транспортного средства по выбранному лепестку.
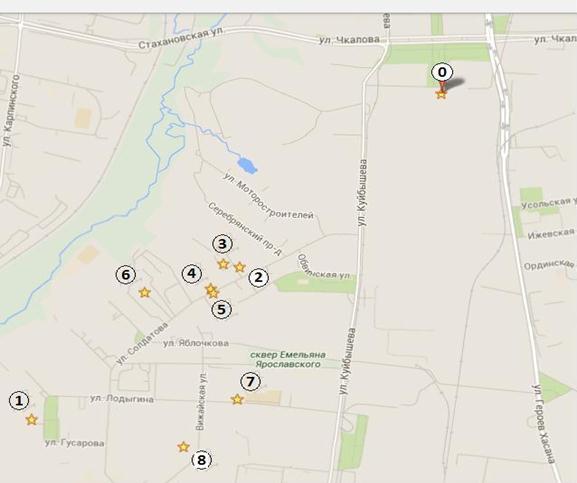
Рис. 2. Маршрут 4 лепестка
Маршрут по лепестку проложен оптимально, кроме переезда из точки 1 в точку 2, так как расстояние между ними больше, чем расстояние от объекта 1 до объекта 6. Такой «скачок» обоснован тем, что пункт 2 открывается раньше, чем пункт 6.
Погрешность получившегося решения составляет 28% по сравнению с теоретически рассчитанным маршрутом. Разница в результатах обосновывается тем, что алгоритм не содержит в себе способов оптимизации работы. Так как в случае, когда вводится ограничение на время, оптимальный план ухудшается, то полученную таким образом погрешность можно считать вполне приемлемой.
Минусом данного алгоритма также является то, что он адаптирован для точек, сконцентрированных на небольшой территории. В коде программы адреса хранения переменных из внешнего файла заданы статически, это может вызвать ряд неудобств, связанных с перекачиванием данных.
Среди положительных особенностей алгоритма стоит выделить учет несимметричности матрицы расстояний; быструю обработку большого объема данных; универсальность, за счет возможности менять входные данные (осуществлять скачивание из других файлов Microsoft Excel); уничтожение обработанных данных из оперативной памяти, после закрытия программы; возможность посмотреть файл с полученными результатами, формирующийся в процессе выполнения алгоритма программой.
Проанализировав полученные результаты, можно сказать, что полученное решение адаптировано для реальных условий, так как затраты транспортных ресурсов являются адекватными; маршруты строятся с учетом выбранных ограничений; имеет место быстродействие программного продукта; но в связи с выявленной погрешностью алгоритм нуждается в доработке с помощью улучшающих методов.
Рецензенты:
Абдулаев А.Р., д.ф.-м.н., профессор, ФГБОУ ВПО «Пермский национальный исследовательский политехнический университет», г. Пермь.
Цаплин А.И., д.т.н., профессор, ФГБОУ ВПО «Пермский национальный исследовательский политехнический университет», г. Пермь.
Библиографическая ссылка
Егорова О.Е., Закирова У.В., Осечкина Т.А. МОДИФИКАЦИЯ ДВУХЭТАПНЫХ АЛГОРИТМОВ ДЛЯ РЕШЕНИЯ ЗАДАЧ МАРШРУТИЗАЦИИ С ВРЕМЕННЫМИ ОКНАМИ // Современные проблемы науки и образования. – 2014. – № 5. ;URL: https://science-education.ru/ru/article/view?id=14563 (дата обращения: 16.04.2024).