Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Губин В.Н. 1

---

1 ФГАОУ ВО «Национальный исследовательский Томский политехнический университет»

В работе рассматривается модель резервирования системы с дискретным временем. В качестве критерия стратегии резервирования выбрано среднее время безотказной работы на бесконечном промежутке. Согласно экспериментальным данным, весь промежуток работы системы разбивается на непересекающиеся промежутки постоянства функции K0(r). Получены условия, при которых оптимальная стратегия состоит во включении двух исправных элементов. Найдены границы интервала, на котором значение оптимальной стратегии K0(r) равно 2. Далее рассмотрен вопрос об оптимальности нулевой стратегии и доказано, что нулевая стратегия для модели резервирования по критерию среднего времени на бесконечном промежутке никогда не является оптимальной. Это означает, что если система работает на бесконечном промежутке, то не следует включать все элементы сразу (если имеется больше двух элементов в резерве). Полученные результаты позволяют сократить алгоритм поиска оптимальной стратегии для рассматриваемой модели резервирования и могут быть использованы на практике для улучшения такого показателя качества системы, как среднее время безотказной работы.

Статья в формате PDF

127 KB

нулевая стратегия

система с дискретным временем

оптимальная стратегия

Модель резервирования

1. Губин В.Н., Травкина В.В. Две задачи динамического резервирования // Вестник Томского государственного университета. Математика и механика. – 2013. – № 5(25). – С. 5-12.

2. Пестов Г.Г., Ушакова Л.В. Оптимальные стратегии в задаче динамического резервирования // Изв. АН СССР. Техническая кибернетика. – 1971. – № 5.

3. Пестов Г.Г., Ушакова Л.В. Исследование оптимальных стратегий в задаче динамического резервирования // Изв. АН СССР. Техническая кибернетика. – 1973. – №5.

4. Чистяков В.П. Курс теории вероятностей. – 5-е изд. – М.: Агар, 2000. – 256с.

5. Беллман Р., Дрейфус С. Прикладные задачи динамического программирования. – М.: Наука, 1985. – 458 с.

6. A. Renyi. Wahrscheinlichkeitsrechnung. Berlin: VEB Deutscher Verlag der Wissenschaften, 1966.

В связи с научно-техническим прогрессом в мире появляются всё новые технические устройства, и, соответственно, возникает необходимость повышения эффективности работы этих технических устройств. В связи с этим все чаще возникают задачи увеличения показателей качества того или иного устройства, таких как среднее время безотказной работы, надежность и другие. Это особенно важно в тех сферах жизни человека, где оборудование является дорогостоящим, труднодоступным или не подлежит ремонту. В данной работе рассматривается одна из таких задач, в которой необходимо указать стратегию оптимального управления резервом, если в наличии осталось небольшое кличество элементов, а также исследовать на оптимальность нулевую стратегию на бесконечном промежутке по критерию среднего времени работы.

Пусть имеется система S с дискретным временем, состоящая из конечного числа параллельно включенных в смысле надежности идентичных элементов. В моменты времени t_k=k Δ, где k = 0, 1, 2, … проводится проверка исправности включенных в работу элементов. Исправные элементы в резерве (не включённые в работу) остаются исправными. Система функционирует на промежутке [1, ∞). Вероятность безотказной работы одного элемента в течение промежутка длиной Δ равна p, вероятность отказа одного элемента за этот же промежуток – q.

Введем характеристики системы:

1) T(k,r) ­– среднее время работы системы при следующей стратегии: в момент начала работы системы из r имеющихся в наличии исправных элементов в работу включается k элементов, после первой проверки используется стратегия, оптимальная по критерию среднего времени безотказной работы;

2) T(r) – среднее время безотказной работы системы при оптимальной стратегии, если в

наличии имеется r исправных элементов;

3) Под K₀(r) будем понимать то количество элементов, которое нужно включить в работу при оптимальной стратегии, если в наличие имеется r исправных элементов.

Тогда по формуле полного математического ожидания [4], [5] имеем:

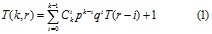
В [1] формула (1) записана в виде сигмы-многочлена:

 ,

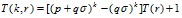где 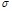 – оператор, действующий на множестве оптимальных стратегий следующим образом:

 .

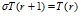Сигма-оператор впервые ввели Пестов Г.Г. и Ушакова Л.В. в своих работах [2,3], в которых исследуются свойства оптимальных стратегий на конечном промежутке и в качестве критерия выбрана вероятность безотказной работы системы.

Требуется определить, с какого момента будет оптимальной следующая стратегия: после каждой проверки в работу включается два элемента, пока система не откажет. Иными словами, сколько должно остаться элементов в резерве для того, чтобы оптимальной стратегией до конца работы системы было постоянное включение двух элементов.

Ясно, что K₀(1)=1. Поскольку K₀(r) возрастает [1], то на некотором промежутке [r1,r2] значение оптимальной стратегии постоянно и равно 2. Покажем, что r₁=2, то есть K₀(2)=2.

Очевидно, что при любом r>1 и 0<p<1 справедливо неравенство T(2,r)-T(1,r)>0, то есть если имеется r исправных элементов, то в работу следует включать не меньше двух элементов. Значит, .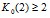

Воспользуемся свойством оптимальных стратегий, изложенным в работе [1].

Теорема 1: Для оптимальной стратегии выполнено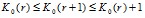 

Из теоремы 1 следует, что K₀(r) возрастает, но не более чем на 1. Отсюда получаем, что K₀(2)=2. Следовательно, при 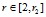, значение K₀(r)=2. Значит, задача сводится к тому, чтобы найти r₂= r₂ (p). Далее потребуется следствие, сформулированное в [1].

Следствие: Если T(r,k-1)≤T(r,k), то k≤ k₀(r); если T(r,k-1)>T(r,k), то k≥ k₀(r).

Так как на отрезке [2,r2] значение K₀(r)=2, то для всех 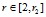 выполнено 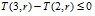. Найдем r₂= r₂ (p) из этого неравенства. Рассмотрим разность

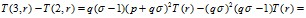
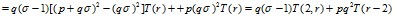
Вычислим T(r) из предположения K₀(r)=2:

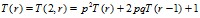
Отсюда получаем рекуррентную формулу для вычисления T(r)

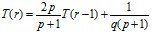
Введем обозначения

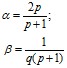
Тогда методом математической индукции можно доказать следующую формулу:

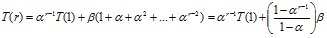
Учитывая, что 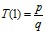, получим

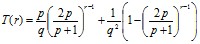
Для удобства преобразуем данное выражение к следующему виду:

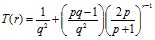 (3)

Так как K₀(r-2)= K₀(r-1)=2 при r > 3, то для вычисления значений T(r-1) и T(r-2) используем также соотношение (3). Имеем

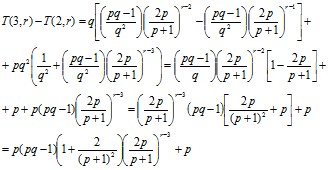 (4)

Таким образом, задача сводится к решению неравенства

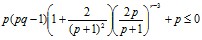
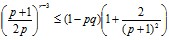(5)

Введем обозначения

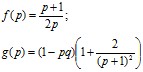
Легко видеть, что f(p)>1 и g(p)>1 при 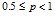. Тогда из неравенства (4) имеем

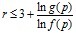  (6)

Следовательно, если 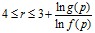, то оптимальное количество элементов, включаемых в работу, равно 2.

Рассмотрим далее задачу об оптимальности нулевой стратегии для введенной выше модели резервирования на бесконечном промежутке.

Определение. Стратегия, при которой все имеющиеся в наличии исправные элементы включаются в работу, называется нулевой стратегией [3].

Изучением вопроса оптимальности нулевой стратегии для модели резервирования на конечном промежутке по критерию надежности занимались в своих работах Пестов Г.Г. и Ушакова Л.В. Ими было найдено условие оптимальности нулевой стратегии, изложенное в работе [3].

В данной работе доказано, что на бесконечном промежутке нулевая стратегия никогда не является оптимальной, в виде следующей теоремы.

Теорема 2. Для любого r>2 справедливо неравенство K₀(r)<r.

Замечание: Неравенство K₀(r)<r означает, что нулевая стратегия для рассматриваемой в данной работе модели никогда не будет оптимальной (если r >2), то есть для того, чтоб система дольше проработала, всегда необходимо оставлять в запасе некоторое количество элементов.

Доказательство.

В силу свойства 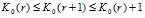 [2] получаем, что

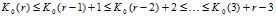 (7)

Покажем, что K₀(3)=2, то есть T(2,3)>T(3,3).

Если K₀(3)=3, то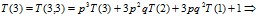 

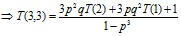 (8)

Если же K₀(3)=2, то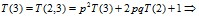 

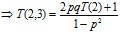 (9)

Определим знак разности T(2,3)-T(3,3). Имеем

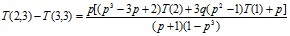 (10)

Так как знаменатель в (9) положителен, определим знак числителя, учитывая, что

.

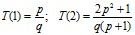Имеем

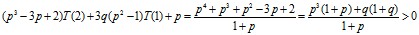
Таким образом, T(2,3)>T(3,3) при любом значении 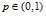. Значит, K₀(3)=2.

Возвращаясь к неравенству (7), имеем

.

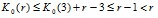Теорема доказана.

Следствие: Для модели резервирования на бесконечном промежутке K₀(3)=2.

Таким образом, если всего имеется три элемента, то расходовать их следует экономно, включая в работу два элемента, до тех пор пока не останется один элемент.

Для вычисления оптимальной стратегии в работе [1] был предложен алгоритм, основанный на использовании метода динамического программирования Беллмана [5], согласно которому на первом шаге вычисляется T(1)=p/q. Далее, используя свойство оптимальных стратегий, можно его упростить. То есть если вычислены значения T(1), T(2), ... , T(r-1) и K0(1), K0(2), ... , K0(r-1), то для нахождения K0(r) следует вычислить два значения: T(K0(r-1)) и T(K0(r-1)+1).

Если T(K0(r-1))> T(K0(r-1)+1), то K0(r)= K0(r-1); если же T(K0(r-1))< T(K0(r-1)+1), то K0(r)= K0(r-1)+1. Таким образом, количество операций на выполнение поиска оптимальной стратегии значительно уменьшается по сравнению с непосредственным перебором.

Выводы:

1. В работе найдены границы промежутка, как функции параметра p, на котором оптимальной стратегией является включение в работу двух элементов.
2. Полученные результаты можно использовать для сокращения алгоритма поиска оптимальной стратегии, предложенного в [1]. А именно, как только в резерве осталось меньше, чем 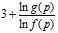   , то в работу постоянно включается 2 элемента.
3. Доказано, что нулевая стратегия для рассматриваемой модели никогда не будет оптимальной (за исключением случаев r=1, 2). Это значит, что хотя бы один элемент всегда нужно оставлять в резерве. Данное свойство также упрощает алгоритм поиска оптимальной стратегии.

Рецензенты:

Трифонов А.Ю., д.ф.-м.н., профессор, профессор кафедры квантовой теории поля физического факультета, ФГБОУ ВПО «Национальный исследовательский Томский государственный университет», г. Томск;

Пестов Г.Г., д.ф.-м.н., профессор, профессор кафедры математического анализа механико-математического факультета, «Национальный исследовательский Томский государственный университет», г. Томск.

Библиографическая ссылка