При оптимальном проектировании козловых кранов одной из задач является определение оптимальной конструкции механизма передвижении крана. Решение данной задачи заключается: в определении оптимальной компоновки механизма, а именно оптимального общего числа ходовых колес zк, количества приводных колес zпр и приводов механизма zдв; выборе оптимальной кинематической схемы привода, определении оптимальной конструкции отдельных элементов привода.
Цель
Целью оптимального проектирования механизмов передвижения козловых кранов является снижение затрат на их изготовление и эксплуатацию.
Материал и методы исследования
Учитывая, что к крановым механизмам предъявляется широкий спектр противоречивых требований, перспективным представляется использование при их проектировании методов многокритериальной оптимизации, позволяющей оценивать различные решения по нескольким параметрам, в частности метода многокритериальной оптимизации, основанного на применении принципа Парето [2, 4]. Для сравнения отдельных решений задачи оптимального проектирования механизма передвижения используется векторный критерий оценки качества решения, включающий в себя параметры, оказывающие непосредственное влияние на технико-экономические свойства машины. В состав векторного критерия для механизма передвижения должны быть включены следующие величины: себестоимость механизма C, как параметр определяющий капитальные затраты на изготовление; масса механизма М, как параметр, определяющий эксплуатационные затраты и стоимость монтажа механизма; КПД механизма η, также оказывающий влияние на эксплуатационные затраты. Требования, предъявляемые к конструкции механизма передвижения и имеющие обязательный характер, задаются в виде ограничений, например, условие обеспечения необходимой прочности узлов механизма.
Суть принципа Парето заключается в том, что среди всех возможных решений механизма X существует некоторое множество решений Pf(X), между которыми лицом, принимающим решения, (ЛПР) не может быть выражено четкое предпочтение. Данное множество называется множеством парето-оптимальных решений или множеством Парето. Любое парето-оптимальное решение превосходит другие парето-оптимальные решения хотя бы по одному из критериев оптимальности, но при этом уступает любому из них также хотя бы по одному другому критерию. В то же время каждое парето-оптимальное решение превосходит любое прочее решение, не вошедшее во множество Парето, по всем критериям. Формирование множества Парето является первой задачей, которую необходимо решить при оптимальном проектировании механизма передвижения крана.
На предварительной стадии лицо, принимающее решения, ЛПР должно определить наиболее перспективные компоновки механизма передвижения и кинематические схемы привода, отличающиеся типом применяемого редуктора или мотора-редуктора, наличием или отсутствием открытой зубчатой передачи, а также способом соединения вала колеса с тихоходным валом редуктора или мотора-редуктора. Механизм передвижения при этом представляется как сложная техническая система, состоящая из отдельных модулей: 1 – модуль электродвигателей и системы управления, 2 – модуль приводных и неприводных колесных установок и кранового рельсового пути, 3 – модуль трансмиссии (включает в себя редуктор, при необходимости соединительные муфты и трансмиссионные валы), 4 – модуль открытой зубчатой передачи (при ее наличии), 5 – модуль тормоза (или тормозов), 6 – объединенный модуль всех металлических конструкций балансиров (при их наличии). Состав модулей может меняться в зависимости от рассматриваемой кинематической схемы привода. Для некоторых компоновок механизма передвижения имеются ограничения по возможности применения различных кинематических схем привода.
Формирование множества парето-оптимальных решений для механизма передвижения следует проводить отдельно для каждого сочетания выбранных ЛПР компоновок механизма передвижения и кинематических схем привода, при этом задача сводится к выбору оптимальных решений для каждого из модулей. В качестве решений для отдельных модулей могут быть рассмотрены как серийно выпускаемые покупные изделия (электродвигатели, колесные установки, редукторы, моторы-редукторы, соединительные муфты и тормоза), так и оригинальные конструкции. При этом должны быть составлены базы данных по всем основным элементам механизма, в состав которой входят все серийно выпускаемые и оригинальные конструкции с указанием их массы, себестоимости, КПД и других параметров.
На каждый из отдельных модулей накладывается своя система ограничений: по прочности, надежности, технологичности, условиям сборки и др. На всю систему механизма передвижения целиком также накладывается ряд ограничений, прежде всего ограничение по заданной техническим заданием скорости передвижения крана. На скорость передвижения крана оказывают влияние: частота вращения вала выбранного электродвигателя nдв, диаметр применяемого ходового колеса Dк, передаточное отношение редуктора uр и открытой зубчатой передачи uоп. При этом изменение одного из перечисленных параметров неизбежно должно сопровождаться изменением какого-либо другого с тем, чтобы в итоге была обеспечена необходимая скорость передвижения крана v. Таким образом, в процессе поиска оптимального решения помимо прочего необходимо определить оптимальные значения вышеперечисленных взаимозависимых параметров. Поставленная задача по своей структуре близка к известной в литературе задаче об оптимальной загрузке судна [5], для решения которой может быть использован метод динамического программирования [1].
Для того, чтобы можно было легко менять распределение указанных выше параметров, определяющих скорость передвижения крана, но имеющих различную размерность, необходим ввести новый безразмерный параметр u, называемый степенью редукции.
Требуемая степень редукции для всей системы определится:
![]()
где nдвmax - максимальная скорость электродвигателя для всех имеющихся в базе данных электродвигателей; Dкmax - максимальный диаметр колеса из всех имеющихся в базе; uрmin, uопmin - минимальные имеющиеся в базе данных значения передаточного отношения редукторов и открытой зубчатой передачи.
Для отдельных решений каждого из модулей степень редукции определится следующим образом:
для 1 го модуля: ![]()
для 2 модуля: ![]()
для 3 модуля: ![]()
для 4 модуля: ![]()
где nдвf, Dкf, uрf, uоп - соответственно обороты двигателя, диаметр ходового колеса, передаточные числа редуктора и открытой передачи для некоторого f-го решения, f – номер решения в базе данных для соответствующего модуля.
Таким образом, условие обеспечения необходимой скорости движения может быть записано в следующем виде
![]() (1)
(1)
где ![]() – степень редукции для некоторого рассматриваемого x-го решения.
– степень редукции для некоторого рассматриваемого x-го решения.
![]()
Предварительно для каждого из модулей должны быть сформированы частные множества парето-оптимальных решений отдельно для каждой степени редукции, в дальнейшем на основе метода динамического программирования, рассматривая сочетания различных частных парето-оптимальных решений для первого и второго модуля, будет составлено общее множество парето-оптимальных решений для двух первых модулей. Далее, рассматривая сочетания полученных общих парето-оптимальных решений для двух первых модулей с частными парето-оптимальными решениями для третьего модуля, формируется множество общих парето-оптимальных решений для первых трех модулей. Повторив аналогичную процедуру для оставшихся модулей, на последнем шаге будет получено множество парето-оптимальных решений для всей системы механизма для рассматриваемого варианта сочетания компоновки механизма с кинематической схемой привода.
Алгоритм формирования множества Парето для отдельного варианта сочетания компоновки механизма передвижения с кинематической схемой приведен на рис. 1. При этом выбрана кинематическая схема, содержащая все возможные модули. Для обозначения отдельных решений вводятся следующие индексы: i - номер рассматриваемого модуля (шага); ji - номер степени редукции для i-го модуля; n - номер частного парето-оптимального решения в формируемом множестве парето-оптимальных решений, полученных для i-го модуля и j-ой степени редукции; s - номер рассматриваемой кинематической схемы; z - номер общего парето-оптимального решения Xiyz, полученного на текущем i-ом шаге при степени редукции y; ki-1 - номер степени редукции для общих парето-оптимальных решений, полученных на предыдущем шаге (при рассмотрении «i-1»-го модуля); m - номер общего парето-оптимального решения Xi-1km, полученного на предыдущем шаге и степени редукции k; yi - степень редукции, получаемая на текущем i-ом шаге при сочетании n-го частного парето-оптимального решения Xijn, полученного для i-го модуля при степени редукции ji с общим парето-оптимальным решением Xi-1km, полученным на предыдущем «i-1»-ом шаге при степени редукции k и имеющим номер m; q - номер рассматриваемой компоновки механизма, s - номер рассматриваемой кинематической схемы.
Для первых трех модулей общие парето-оптимальные решения образуются как сочетание частных парето-оптимальных решений для рассматриваемого модуля Xijn с общими парето-оптимальными решениями, полученными на предыдущем шаге (для всех уже рассмотренных ранее модулей) Xi-1km.. Степени редукции рассматриваемого общего решения u сравниваются с полученными ранее uy (блок 10). Если подобная степень редукции ранее встречалась, то рассматриваемое решение сравнивается с полученными ранее парето-оптимальными решениями Xiyz с той же степенью редукции uy (блоки 15, 16). Если данная степень редукции получена впервые, решение запоминается как первое парето-оптимальное решение с этой степенью редукции (блок 13). В результате формируются множества парето-оптимальных решений на каждом шаге, вплоть до четвертого. На четвертом шаге для каждого из общих парето-оптимальных решений, полученных для трех первых модулей, определяются оптимальные параметры открытой зубчатой передачи таким образом, чтобы обеспечить заданную скорость передвижения крана (блок 35).
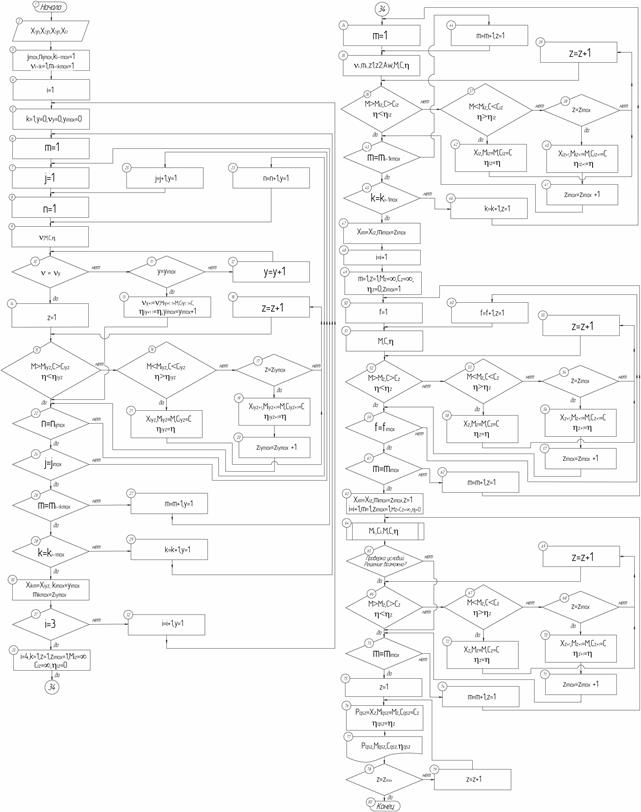
Рис. 1. Блок-схема алгоритма формирования множества парето-оптимальных решений
Все полученные на четвертом шаге решения будут иметь одинаковую степень редукции, поэтому могут быть обозначены просто X4z Сравнивая все полученные решения с помощью аналогичного алгоритма (блоки 36, 37), формируем множество общих парето-оптимальных решений для первых четырех модулей. На пятом шаге для каждого решения рассматриваются различные варианты тормоза, полученные решения сравниваются между собой (блоки 52, 53), в результате получаем множество общих парето-оптимальных на 5-м шаге (блоки 56, 58) На последнем шаге для каждого полученного парето-оптимального решения в специальной подпрограмме определяются оптимальные конструкции балансиров для многоколесных систем (блок 64), вычисляются общие значения массы М и себестоимости С механизма. При этом каждое полученное решение окончательно проверяется по всем ограничениям, накладываемым на всю систему привода (блок 65). Решения, удовлетворяющие всем условиям, сравниваются между собой по алгоритму, уже использованному ранее (блоки 66, 67). В итоге формируется область общих парето-оптимальных решений для всей системы для сочетания q-ой компоновки механизма с s-ой кинематической схемой привода (блоки 70, 72).
Для кинематических схем, не содержащих открытую зубчатую передачу, на третьем шаге при выборе редуктора проверяется выполнение условия (1), после чего исключаются общие решения для трех первых модулей, не обеспечивающие заданную скорость передвижения. После этого, минуя четвертый шаг, сразу осуществляется переход к пятому и далее к шестому шагу.
На последующей стадии сравниваются между собой все общие парето-оптимальные решения, полученные для разных сочетаний компоновок механизма q с кинематическими схемами привода s алгоритму, подобному приведенному выше; решения, уступающие какому либо другому по всем параметрам векторного критерия, исключаются. В итоге окончательно формируется множество парето-оптимальных решений для механизма передвижения.
Из полученного множества Парето для механизма передвижения ЛПР должно выбрать окончательное решение, в случае если полученное множество Парето окажется слишком широким для того, чтобы ЛПР смогло совершить осознанный выбор, необходимо воспользоваться одним из известных методов сужения множества Парето [3].
Заключение
Предложенный метод оптимального проектирования имеет следующие преимущества: позволяет автоматизировано рассмотреть при проектировании механизма передвижения применение различных всех перспективных по мнению ЛПР компоновок механизма, кинематических схем привода, а также всех доступных на конкретном заводе-изготовителе комплектующих механизма, что в режиме «ручного» проектирования практически невозможно из-за ограниченных сроков подготовки технического проекта; применение для поиска оптимального решения динамического программирования позволяет существенно сократить время поиска по сравнению с методом последовательного перебора, при этом гарантируя нахождение глобального экстремума по каждому из рассматриваемых критериев оптимальности.
Рецензенты :
Хальфин М.Н., д.т.н., профессор, заведующий кафедрой «Подъемно-транспортные, строительные и дорожные машины» Южно-Российского государственного политехнического университета (НПИ) имени М.И. Платова, г. Новочеркасск.
Самохвалов В.Н., д.т.н., профессор, заведующий кафедрой «Строительные, дорожные машины и технология машиностроения» Самарского государственного университета путей сообщения, г. Самара.
Библиографическая ссылка
Кобзев Р.А. МНОГОКРИТЕРИАЛЬНОЕ ОПТИМАЛЬНОЕ ПРОЕКТИРОВАНИЕ МЕХАНИЗМОВ ПЕРЕДВИЖЕНИЯ КОЗЛОВЫХ КРАНОВ С ПРИМЕНЕНИЕМ ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ // Современные проблемы науки и образования. 2014. № 4. ;URL: https://science-education.ru/ru/article/view?id=14368 (дата обращения: 14.03.2026).



