В современном обществе рынок труда требует всё новых знаний от молодых специалистов. При их обучении в вузе приходится вводить в учебный план новые дисциплины взамен старых, а нередко вовсе начинать обучение по новому направлению. При этом надо соблюдать многочисленные требования государственного стандарта высшего образования: ограничения на суммарный объем дисциплин в семестре, число форм контроля и другие. Возникает нелегкая задача разработки многочисленных учебных планов.
В числе других факторов учебного плана (объем, наличие курсовых или контрольных работ) на успешность усвоения студентами дисциплин оказывает влияние последовательность их изучения.
Целью данной работы является моделирование качества получаемых студентами знаний для изучения возможностей автоматизации составления учебных планов. Для этого решается задача формального описания последовательности освоения дисциплин. Используется математический аппарат временных иерархических раскрашенных сетей Петри (РСП) [3]. Данный аппарат позволяет наглядно представить различные события, что в свою очередь может привести к применению когнитивных технологий.
Для моделирования учебного процесса сети Петри использованы в [1]. Здесь в пределах семестра оцениваются контрольные и лабораторные работы, посещение и пропуск занятий в баллах, принимается решение деканатом о переводе на другой семестр, но целиком учебный план не моделируется.
Моделирование
Смоделируем зависимость качества подготовки специалистов от последовательности изучения предметов с помощью РСП (рис. 1). Согласно рабочим программам дисциплин, они формируют свои компетенции, см. стандарт [4], номера которых представим цветом l маркеров в позициях сети (табл. 1). Например, компетенция ОК-1 такая: «Способен использовать, обобщать и анализировать информацию ... ». Компетенции необходимы для профессиональной деятельности выпускника и успешного изучения других дисциплин (или их разделов, если рассматривается отдельно взятая дисциплина).
Рассмотрим пример. В Чувашском государственном университете для бакалавров по профилю «Прикладная информатика» начало изучения дисциплины «Основы теории управления» (ОТУ) запланировано с 1 курса. Это слишком рано, так как ее изучение должно базироваться на знаниях и умениях, приобретённых при изучении курсов «Математика», «Теория вероятностей и математическая статистика», «Основы теории цепей». Согласно рабочей программе, изучение ОТУ означает формирование следующих общекультурных компетенций: ОК-1, ОК-2, ОК-5, ОК-10, и профессиональных компетенций: ПК-3, ПК-9, ПК-17, ПК-20, ПК-21, ПК-22. Математика формирует компетенции ОК-1 и ПК-10. Теория вероятностей и математическая статистика – ОК-1, ОК-5 и основана на входных знаниях ОК-2, ОК-9, ОК-10, ПК-20.
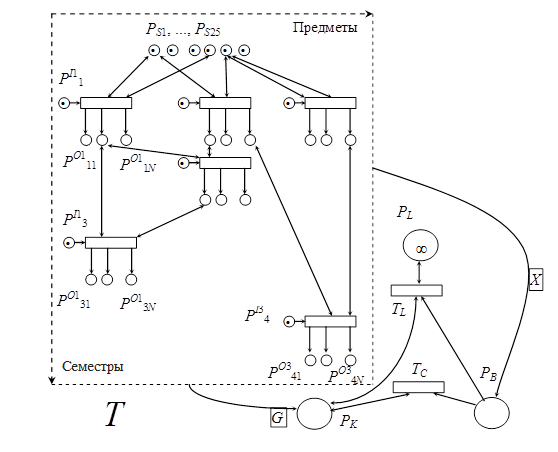
Рис. 1. Модель усвоения и применения знаний
T - иерархический переход, означающий выполнение учебного плана;
PS1, ..., PS25 - позиции, соответствующие школьным знаниям;
POijk - позиция, предназначенная для k-й компетенции, формируемой i-й дисциплиной в j-м семестре, где k = 1, ..., N (N - число компетенций), i = 1, ..., 3, j = 1, ...,4;
PIij - позиция, содержащая набор факторов для преподавания i-го предмета в j-м семестре;
PB - позиция для хранения профессиональных запросов;
PK - позиция, содержащая модель группы выпущенных специалистов;
PL - позиция, содержащая информацию Интернета, библиотеки и т.п.;
TL - переход, означающий использование библиотеки, Интернета и т.д.;
TC - переход, означающий быстрое выполнение профессионального запроса компетентным специалистом;
X - кратность дуги, означающая количество профессиональных запросов.
Школьные знания представлены цветами c маркеров в позициях PS1, ..., PS25 (по числу школьных предметов). И школьные знания, и полученные в вузе со временем забываются [5]. Введем эффект забывания x1, характеризующий память студентов, например, x1=0.1. Для простоты будем считать, что эффективность компетенцииχ’ = χ – wx1, (1)
где w – число семестров, прошедших со времени последнего обращения к маркеру. Время отложено по оси ординат, дискретно и представлено семестрами. Последовательность срабатывания переходов определяется, согласно данной оси, т.е. первыми срабатывают самые верхние, а последними – нижние переходы. Подобные дополнительные правила для переходов описаны по ходу изложения.
По оси абсцисс отложены номера изучаемых предметов. Это упрощенный рисунок, здесь показаны только три предмета и четыре семестра. Схему можно продолжить рисовать далее в ширину и высоту.
Сеть иерархическая: часть, охваченная пунктиром, образует иерархический переход T. Позиция POijk на выходе любого перехода внутри T предназначена для k–й компетенции, формируемой i–й дисциплиной в j–м семестре. Здесь k = 1, ..., N, где N – число компетенций, i = 1, ..., 3, j = 1, ...,4. Маркера в этой позиции пока нет, но когда он появится, то будет означать компетенцию, определяемую расположением позиции. Например, крайняя левая позиция предназначена для ОК-1.
Если студент что-то выучит плохо, значит, будет меньше цвет χ маркера. Это число связано с полученной оценкой, но не равно ей вследствие необъективности оценивания. Стрелки обратно означают, что компетенция не исчезает, напротив, освежение ее в памяти при использовании приводит к подкреплению. Из рисунка следует, что каждый из переходов внутри T может сработать только один раз и представляет собой изучение дисциплины в течение семестра и промежуточный контроль (зачет, экзамен).
Позиция PIij слева такого перехода содержит набор факторов для преподавания i-го предмета в j-м семестре как цвета маркера. Эти цвета оказывают влияние на цвет выходного маркера c операцией «нечеткий минимум»:
χ = min{μ(α), μ(β), μ(δ), μ(γ), μ(ε), μ(ν), μ(φ), μ(χ")},
где μ – функция принадлежности, χ” – минимальная из эффективностей компетенций χ’ во всех входных позициях, определяемых по (1).
Например, если расписание хорошее (μ(γ) ≈ 0.9), а учебно-лабораторная база плоховата (μ(δ) ≈ 0.6), и для простоты не учитывать остальные условия, то минимум из них χ=0.6. Формы графиков μ должны учитывать, что например, даже если аудитории плохие, студенты все равно сдают зачет и что-то узнают.
Отсутствие возбужденных переходов в переходе T означает, что он сработал. При этом все маркеры из всех позиций POijk объединяются и помещаются в виде маркера в позицию PK, причем, если у них одинаковые компетенции, они объединяются операцией «max» для χ. Это делается столько раз, сколько студентов в группе (G).
Пусть, например, Математика в 1 семестре сформировала ОК-1 с цветом 0.7. Теория вероятностей и математическая статистика во 2 семестре – 0.5. ОТУ в 3 семестре – 0.5. Бакалавры сокращенного срока обучения выпускаются после 6 семестра, и так как x1=0.1, от цвета Математики остается 0.7-0.1*6=0.1, от ОТУ – 0.2. Освеженные в памяти компетенции препятствуют снижению цвета маркера при учете забывания. Так, если ОТУ использовало компетенцию от предмета «Теория вероятностей и математическая статистика», то это продлевает на 3 семестр компетенцию со значением 0.5, и от данного предмета тоже останется 0.2. Из полученных цветов max{0.1, 0.2, 0, 0.2} = 0.2, это и есть остаточные знания по данной компетенции, или цвет маркера.
Таблица 1
Цвета маркеров
|
№ п.п. |
Позиция |
Цвет (атрибут) или их набор |
|
1. |
POijk |
χ – вещественное число, оценивающее компетенцию |
|
2. |
PIij |
α – размер оплаты преподавателю, β – квалификация преподавателя, δ – учебно-лабораторная база, γ – качество расписания занятий по предмету, ε - морально-психологическая обстановка, ν – объем (зачетных единиц трудоемкости), φ – наличие курсовых или контрольных работ |
|
3. |
PSi |
χ – вещественное число, оценивающее уровень знания i-го школьного предмета |
|
4. |
PK |
Четверка {χ, ΛS, Ω, θ}, где χ={χ1, χ2, ...} – множество вещественных чисел, оценивающих ту или иную компетенцию конкретного выпускника; ΛS={λ1, λ2, ...} – набор номеров компетенций специалиста; Ω = {ω1, ω2, ...} – набор текстов компетенций; θ – место трудоустройства. Номера элементов χ, ΛS и Ω привязаны друг к другу, их число одинаково. |
|
5. |
PB |
ΛB={λ1, λ2, ...} – набор компетенций, необходимых для выполнения поручения, q – место трудоустройства |
|
6. |
PL |
λ – номер компетенции |
|
7. |
PM |
t – время обработки запроса |
Рассмотрим часть сети Петри вне T, это временная сеть Петри. После срабатывания T появляется возможность обработки многочисленных поручений работодателей, это моделируется появлением X маркеров со случайным набором атрибутов в позиции PB. Выпускается группа специалистов, что моделируется появлением G маркеров в позиции PK. При этом специалисты сразу трудоустраиваются, т.е. их атрибуты θq принимают какие-либо из сгенерированных значений атрибута θ маркеров в PB.
Переход TC означает, что в соответствии с поступившим из PB профессиональным запросом (например, таким как разработка какого-либо программного модуля) специалист компетентен и может быстро его выполнить. Переход TC вначале сравнивает реквизиты запроса (номера компетенций) с атрибутами одного из маркеров в позиции PK. Обозначим его Mg(Pk), он моделирует знания случайно выбранного выпускника, трудоустроенного в соответствии с атрибутом θ маркера из PB. Таких компетенций может и не быть по стандарту. Если есть совпадение, причем для каждого элемента LB цвет c соответствующего элемента множества C выбранного маркера на удовлетворительном уровне x5, например, x5=0.2, то переход срабатывает за короткое время. Соответствие определяется по номеру компетенции или, если такого номера нет, по смыслу текста (области знаний из стандартного классификатора).
Если нет совпадения, TC не возбужден, тогда срабатывает переход TL. Он означает необходимость воспользоваться библиотекой, Интернетом, советами коллег или даже провести небольшое исследование. Время его работы значительно больше, чем у TC. При срабатывании TL также освежаются знания, полученные по диплому, поэтому Mg(Pk) для соответствующего цвета λh увеличивает цвет χh: χh=min{1, χh+x3}, где x3 – некоторая константа, например, 0.2. Может приобретаться новый опыт, не входящий ни в одну компетенцию. Тогда Mg(Pk), для своего ωh, наиболее близкого по смыслу этому опыту, добавляет новую часть, причем устанавливается цвет χh, в некоторую константу x4, например, в значение 0.5, так как для хорошего усвоения требуется повторение.
Старые знания склонны к забыванию, а также к моральному устареванию. Т.е. при срабатывании TL для всех маркеров в PK и ∀h, χh=χh–x6, где x6 – некоторая константа забывания, например, равная 0.0001. Если не удается удовлетворить профессиональные нужды забытыми или морально устаревшими знаниями lh из позиции PK, последние попутно обновляются, используя переход TL. Это обновление происходит не до максимума χ. Так как только многократное повторение данного запроса приводит к прочному запоминанию правил удовлетворения запроса, то в данном случае для простоты воспользуемся формулой: χh =min{1, χh +x2}, где x2 – некоторое число, зависящее от умственных способностей специалистов, например, 0.2. Средняя скорость время работы сети оценивает среднюю производительность специалистов. Чтобы она сразу по выпуску была высокой, нужно обеспечить хороший учебный план, расписание и прочие условия для обучения.
Цвета маркеров в позициях PIij могут зависеть от эффективности работы специалистов. Эффективность определяется работодателями и формирует то или иное общественное мнение, оказывающее давление на руководство вуза. Последнее может выплачивать премии преподавателям, обновлять оборудование, ремонтировать аудитории. Эта зависимость сложная и косвенная, поэтому, вначале для простоты можно принять, что цвета всегда являются одинаковыми, тем не менее, их надо установить в соответствии с реальными значениями. Связь с работодателем существует и прямая, когда студенты направляются на практику на предприятие. В этом случае при генерации атрибутов ΛS маркеров в PK нужно заранее дополнять тексты компетенций Ω в соответствии с сгенерированными для соответствующего работодателя θ.
При составлении учебного плана важно руководствоваться принципом оптимизации структуры перехода T приведенной на рис. 1 сети Петри в смысле компромиссного знания выпускниками всех дисциплин учебного плана. Кроме этого, нужно оптимизировать распределение курсовых и контрольных работ, а также зачетных единиц трудоемкости по дисциплинам, т. е. имеются различные распределяемые ресурсы, ограничения стандарта и время размещения дисциплин в плане. Этим задача напоминает задачу составления расписания, где также распределяются ресурсы, время размещения, ограничения, но только добавляется периодичность.
Знаний в голове у студентов останется тем больше, чем, в частности, лучше составлены учебный план и расписание. Расписание занятий уже давно составляется автоматически. Разработана программа составления расписания учебных занятий, использующая алгоритм, предложенный в [2]. В нем имеет решающее значение последовательность выборки занятий для их размещения, так как плохая последовательность может привести к локальному экстремуму целевой функции расписания, довольно далекому от глобального по значению критерия качества. Использование вышеприведенной сети Петри также показывает важность выбора разумной последовательности каких-либо событий для хорошего качества итогового результата.
Заключение
Предложенная математическая модель показывает важность правильного планирования последовательности изучения студентами дисциплин учебного плана. Предложенная сеть Петри моделирует также социальную систему по подготовке кадров и их использованию в народном хозяйстве.
Она получена из двух самостоятельных фрагментов – иерархического перехода, моделирующего выполнение учебного плана, и модели обновления полученных знаний. Эти фрагменты затем соединены друг с другом, а также замкнуты при помощи обратной связи, что стало возможным благодаря наглядности сетей Петри, что, в сущности, и есть использование когнитивной технологии. Хотя данная раскрашенная сеть Петри является расширением классических сетей Петри, она не используют ингибиторных дуг.
В процессе создания хороших условий для обучения принцип поиска правильной последовательности важно соблюсти не только относительно выбора времени изучения дисциплин, но и для формирования хорошего расписания занятий (последовательность их выбора для помещения в сетку часов).
Практическая значимость применения новой модели в том, что она направлена на улучшение качества подготовки молодых специалистов.
Рецензенты:
Афанасьев А.А., д.т.н., профессор кафедры автоматики и управления в технических системах ФГБОУ ВПО «Чувашский государственный университет им. И.Н. Ульянова», г. Чебоксары.
Охоткин Г.П., д.т.н., профессор, декан факультета радиоэлектроники и автоматики ФГБОУ ВПО «Чувашский государственный университет им. И.Н.Ульянова», г. Чебоксары.
Библиографическая ссылка
Димитриев А.П. МОДЕЛИРОВАНИЕ УСВОЕНИЯ И ПРИМЕНЕНИЯ УЧЕБНОГО МАТЕРИАЛА НА РАСКРАШЕННЫХ СЕТЯХ ПЕТРИ // Современные проблемы науки и образования. 2014. № 4. ;URL: https://science-education.ru/ru/article/view?id=14367 (дата обращения: 06.03.2026).



