Проблема оперативного и точного определения местоположения движущихся объектов была и остаётся одной из основных при решении задач навигации летательных аппаратов, кораблей, прочих транспортных средств.
При этом постоянно растущая интенсивность транспортных потоков на улицах городов, в воздушном пространстве и акваториях портов обуславливает непрерывное повышение требований к точности определения навигационных параметров.
Принципы построения навигационных систем, использующих радиояркостные карты местности, подробно рассмотрены в работах [6-9].
В то же время в сложной современной помеховой обстановке в последние десятилетия одними из основных средств навигации на большинстве видов подвижных объектов стали инерциальные навигационные системы (ИНС). Наиболее востребованными и привлекательными для беспилотных летательных аппаратов являются бесплатформенные инерциальные навигационные системы (БИНС) [5], концептуальное рассмотрение которых и составляет основное содержание данной статьи.
Перед другими навигационными системами ИНС имеют такие преимущества, как:
-
высокая информативность и универсальность применения (ИНС определяет всю совокупность пилотажно-навигационных параметров, необходимых для управления ЛА),
-
полная автономность действия,
-
высокая помехозащищенность,
-
возможность высокоскоростной выдачи информации (до 100 Гц и выше).
Так называемые бесплатформенные ИНС (БИНС), которые не используют для стабилизации своих инерциальных датчиков таких сложных и дорогостоящих технических устройств, как гиростабилизированные платформы, особенно интенсивно развивались в последнее время.
К числу потенциальных преимуществ БИНС по сравнению с платформенными ИНС можно отнести:
-
меньшие размеры, массу и энергоемкость;
-
существенное упрощение механической части системы и ее компоновки и, как следствие, повышение надежности системы;
-
сокращение времени установки начальных параметров;
-
универсальность системы, поскольку переход к определению тех или иных параметров навигации осуществляется алгоритмически.
В соответствии с принципами, которыми пользуются при разработке и реализации инерциальных систем, различают следующие их типы.
-
В геометрических системах платформа стабилизирована таким образом, что ее абсолютная угловая скорость равна нулю. При этом ориентация платформы относительно инерциальной системы координат остается неизменной. В таких системах рама вращается с помощью часового механизма вокруг земной оси, сохраняющей неизменное направление в инерциальном пространстве. Скорость вращения рамы равна угловой скорости Земли Ωз, так что рама остается параллельной некоторой плоскости меридиана.
-
В аналитических системах гироскопы и акселерометры смонтированы жестко на объекте. Эти системы называют бескарданными или бесплатформенными инерциальными системами. Угловые скорости объекта измеряются гироскопами, а переносные ускорения – акселерометрами. Вычислитель «запоминает» начальную ориентацию и определяет местоположение объекта в любой момент времени.
Для всех типов систем необходим вычислитель, чтобы рассчитывать координаты места движущегося объекта.
Толкование инерциальной навигации следует из рассмотрения задачи определения положения объекта на плоской поверхности. В соответствии с первым законом Ньютона движущийся по плоской поверхности объект при отсутствии действующей на него силы пребывает в состоянии прямолинейного движения с постоянной скоростью. Зная начальные условия, то есть начальное положение объекта, его курс и скорость, можно определить текущее положение движущегося объекта в зависимости от времени [3].
Второй закон Ньютона устанавливает, что направление движения изменяется под действием приложенной к объекту силы. При этом ускорение направлено по линии действия силы. В декартовых координатах второй закон Ньютона выражается в форме:
![]() или
или ![]()
Эти соотношения применительно к движущемуся объекту связывают силу тяги, массу объекта и производную по времени от скорости (ускорение). Измерения ẍ и ÿ с последующим интегрированием дают значения приращений, составляющих скорости ẋ и ẏ. Эти приращения добавляются к начальным значениям ẋ0 и ẏ0 и дают составляющие текущей скорости. Интегрирование же составляющих скорости позволяет получить соответствующие приращения начальных значений координат x и y. Так определяется текущее местоположение объекта. Для пояснения принципа инерциальной навигации рассмотрим работу элементарного акселерометра на следующем примере. Человек в равномерно движущемся лифте наблюдает за массой, подвешенной к потолку на пружине, и пытается определить характер своего движения на основании отклонения пружины. Если масса m, а ускорение свободного падения g, то пружина растягивается силой mg. Если лифт движется с ускорением a, то пружина будет дополнительно нагружена силой ma, направление которой зависит от знака ускорения. Наблюдатель без дополнительных данных не в состоянии определить причину растяжения пружины (гравитационная сила, сила тяги подъемника или совокупность обеих сил). В общем случае растяжение пружины эквивалентно величине mg-ma, где g и a имеют положительное значение, будучи направленными вниз. При движении лифта с ускорением вверх сила, действующая на массу, равна mg-ma=m(g-a)=mf[4]/
Величина f называется кажущимся ускорением. Приведенные рассуждения справедливы при проектировании ускорений на вертикальную ось. Величина f может быть представлена в виде векторного уравнения![]() . Акселерометр измеряет только кажущееся ускорение, то есть разность между абсолютным и гравитационным ускорениями (ускорением свободного падения). Это обстоятельство принципиально затрудняет реализацию инерциальных систем, потому что для вычисления пути необходимо исключить из показаний акселерометра гравитационные ускорения. Для простейшего случая навигации на плоской поверхности в декартовой системе координат, когда объект находится в состоянии покоя, один из таких акселерометров располагается по оси Х, другой – по оси Y[3]/
. Акселерометр измеряет только кажущееся ускорение, то есть разность между абсолютным и гравитационным ускорениями (ускорением свободного падения). Это обстоятельство принципиально затрудняет реализацию инерциальных систем, потому что для вычисления пути необходимо исключить из показаний акселерометра гравитационные ускорения. Для простейшего случая навигации на плоской поверхности в декартовой системе координат, когда объект находится в состоянии покоя, один из таких акселерометров располагается по оси Х, другой – по оси Y[3]/
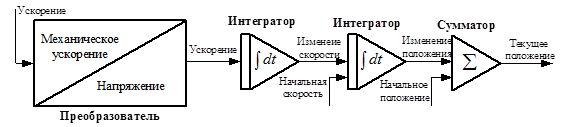
Рис.1. Схема одноканальной инерциальной навигации на плоской поверхности
Двойное интегрирование выходных сигналов этих акселерометров дает приращение координат X и Y в функции времени.
Упрощенная схема одноканальной инерциальной системы на плоской поверхности (рис. 1) имеет в своем составе акселерометр, первый и второй интеграторы, датчик начальных условий (скорости и координат), а также вычислитель-сумматор.
Если гравитационные ускорения не учтены или не исключены, то возникают следующие погрешности.
Погрешность в азимуте. Положение оси чувствительности акселерометра по азимуту должно быть известно до того, как его выходной сигнал может использоваться в процессе решения навигационной задачи. Пусть платформа, на которой установлен акселерометр, смещена по азимуту на некоторый малый угол ![]() (рис. 2). Тогда, если импульс начального ускорения, которое испытывает движущийся объект, связан с движением вдоль линии ОА, выходная информация акселерометра интерпретируется неверно, регистрируя движение вдоль линии 0В. Указанная ошибка CD в определении координат объекта является линейной функцией произведения начальной ошибки в определении азимута на пройденную дальность [2].
(рис. 2). Тогда, если импульс начального ускорения, которое испытывает движущийся объект, связан с движением вдоль линии ОА, выходная информация акселерометра интерпретируется неверно, регистрируя движение вдоль линии 0В. Указанная ошибка CD в определении координат объекта является линейной функцией произведения начальной ошибки в определении азимута на пройденную дальность [2].

Рис. 2. К определению ошибки выставки акселерометров в азимут
Погрешность определения горизонта. Влияние азимутальной погрешности на решение навигационной задачи выражается достаточно просто. Погрешности определения горизонта, влияние которых проследить несколько сложнее, создают, однако, в самолетной навигации более серьезные ошибки. Для рассматриваемого случая плоской Земли предположим, что гравитационное ускорение ![]() перпендикулярно плоской поверхности. Тогда, если платформа горизонтальна, то ось чувствительности акселерометра параллельна поверхности Земли, и инерционная масса акселерометра не смещается относительно начального положения.
перпендикулярно плоской поверхности. Тогда, если платформа горизонтальна, то ось чувствительности акселерометра параллельна поверхности Земли, и инерционная масса акселерометра не смещается относительно начального положения.
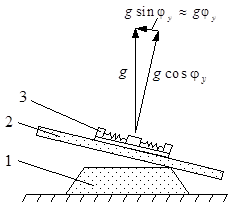
Рис. 3. Влияние отклонения платформы в горизонтальной плоскости
Если платформа 2 смещена относительно оси ![]() на достаточно малый угол
на достаточно малый угол ![]() (рис. 3), то допустимо приближение
(рис. 3), то допустимо приближение ![]() , при этом основная составляющая силы тяжести чувствительной массы акселерометра 3 воспринимается основанием 1 прибора. Но вторая составляющая действует вдоль оси чувствительности акселерометра и интерпретируется как действительное ускорение объекта и после двойного интегрирования дает ошибочные данные об изменении положения объекта.
, при этом основная составляющая силы тяжести чувствительной массы акселерометра 3 воспринимается основанием 1 прибора. Но вторая составляющая действует вдоль оси чувствительности акселерометра и интерпретируется как действительное ускорение объекта и после двойного интегрирования дает ошибочные данные об изменении положения объекта.
Обобщенные функциональные схемы БИНС приведены на (рис. 4 и 5). На (рис. 4) показана обобщенная структура системы, работающей в инерциальной системе координат. Информация с блока гироскопов (БГ) в виде проекций вектора угловой скорости ΩΒ на связанные с объектом оси используется в алгоритме ориентации (АО) для формирования матрицы А направляющих косинусов между связанными и инерциальными осями.
Данные с блока акселерометров (БА) в виде проекций вектора кажущегося ускорения nB на связанные с объектом оси в блоке пересчета (БП) пересчитываются к инерциальным осям с использованием полученной матрицы ориентации. Вычисленные проекции кажущегося ускорения на инерциальные оси (полученный вектор n1) передаются в блок решения навигационного алгоритма (НА). Выходные параметры БИНС в этом случае представляются инерциальными декартовыми координатами радиус-вектора местоположения RI = [XI,YI,ZI]T, проекциями абсолютной скорости движения VI = [VxI,VyI,VzI]T, а также матрицей ориентации объекта в выбранной инерциальной системе координат А[1].
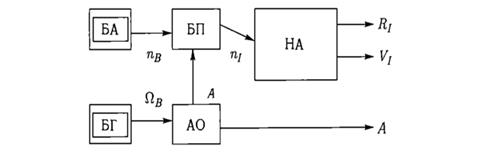
Рис. 4. Обобщенная блок-схема БИНС, работающая в инерциальной системе координат
Вторая типовая схема построения БИНС представлена на (рис. 5). Этот вариант реализует алгоритм системы, работающей во вращающейся (наиболее часто – горизонтальной) системе координат.
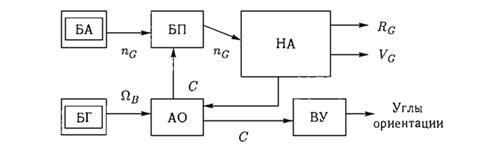
Рис. 5. Обобщенная блок-схема БИНС, работающая во вращающейся системе координат
Как и в предыдущем случае, информация с БГ в виде проекций вектора угловой скорости ΩΒ подаётся на связанные с объектом оси, используется в АО. Однако на этот раз определяется матрица С направляющих косинусов между связанными осями и осями, которые вращаются с угловой скоростью ΩG. Это приводит к необходимости модифицировать алгоритм ориентации и привлечь для его реализации вычисленные в НА проекции вектора ΩG, что отображено на схеме дополнительной связью. Информация с БА в виде проекций вектора кажущегося ускорения nG на связанные с объектом оси передается в БП для приведения к навигационным осям с использованием полученной матрицы ориентации С. Вычисленные проекции (полученный вектор nG) передаются в блок решения НА, в зависимости от вида определяемой скорости. На выходе БИНС формируется радиус-вектор местоположения объекта RG, вектор скорости VG = [VXG,VYG,VZG], a также углы ориентации.
В частном случае, когда в качестве навигационного базиса выбран горизонтный, ориентированный по странам света трехгранник, на выходе системы будут сформированы географические координаты радиус-вектора местоположения Rg = [φ,λ,h], проекции относительной скорости движения UG = [UN,UE,UZ], а также углы ориентации объекта в географической системе координат – истинный курс ψ, тангаж υ и крен γ [5].
В обоих рассмотренных вариантах, которые можно считать типовыми, показания акселерометров предварительно приводились к осям навигационного базиса (инерциального или вращающегося). Можно предложить алгоритмы, когда ведется прямое интегрирование показаний акселерометров в связанных с объектом осях. Однако в этом случае потребуется большая скорость обработки навигационных данных, поскольку угловое движение беспилотных маневренных летательных аппаратов рассматриваемых классов является достаточно динамичным и, как следствие, проекции вектора кажущегося ускорения η на связанные с аппаратом оси меняются быстро (угловые скорости могут достигать 360 °/с). В приведенных выше схемах эта проблема, в известной степени, снимается за счет проецирования вектора кажущегося ускорения на навигационный базис, т. к. угловая скорость этого базиса существенно меньше, чем связанного, и проекции вектора n на нем меняются с меньшей скоростью. Тем не менее, учитывая бурное развитие вычислительных средств, схема прямого интегрирования показаний акселерометров может быть реализована, хотя в настоящее время серийно подобные БИНС не выпускаются.
Заключение
В работе рассмотрены основные принципы построения беспилотных инерциальных навигационных систем, с помощью которых могут решаться задачи определения местоположения различных движущихся объектов.
Рецензенты:
Поршнев С.В., д.т.н., профессор, зав. кафедрой радиоэлектронных информационных систем, ФГАОУ ВПО «Уральский федеральный университет имени первого Президента России Б.Н. Ельцина», г. Екатеринбург.
Иванов В.Э., д.т.н., профессор, зав. кафедрой технологий средств связи, ФГАОУ ВПО «Уральский федеральный университет имени первого Президента России Б.Н. Ельцина», г. Екатеринбург.
Библиографическая ссылка
Доросинский Л.Г., Богданов Л.А. ОСНОВЫ И ПРИНЦИПЫ ПОСТРОЕНИЯ ИНЕРЦИАЛЬНЫХ НАВИГАЦИОННЫХ СИСТЕМ // Современные проблемы науки и образования. 2014. № 5. ;URL: https://science-education.ru/ru/article/view?id=14356 (дата обращения: 09.02.2026).



