Мы считаем, что один из возможных подходов в решении данной проблемы в применении к математическим дисциплинам - развитие понимания сути рассматриваемой проблемы, в том числе на интуитивном уровне. С этой целью следует вводить в процесс преподавания проведение простейших вычислительных экспериментов и визуализацию результатов, в том числе с применением современных пакетов вычислительной математики. Наиболее удобной нам представляется система WolframAlpha, которая является облачным сервисом всемирно известной системы Mathematica. Основное достоинство сервиса - возможность осуществлять вычисления, не устанавливая систему на свой персональный компьютер. Для вычислений достаточно зайти на сайт [4].
В данной работе мы демонстрируем применение системы WolframAlpha для иллюстрации понятия фрактала и элементов теории графов.
Фракталы
Понятие фрактала было введено Бенуа Мандельбротом. Фракталы представляют собой структуры, имеющие определенные особенности и свойства, такие как самоподобие (которое делает фрактал масштабно-инвариантным) и масштабирование по степенному закону [2, 3]. В соответствии с этими особенностями фрактальные зависимости имеют вид прямой на графиках, где обе оси имеют логарифмический масштаб. Размерность фрактала не обязательно является целым числом. Так, фрактальная размерность детерминистического процесса равна 1, а случайного - 1,5.
Продемонстрировать наглядно фрактал можно на примере упомянутого в [3] фрактала, называемого салфеткой Серпинского (рис. 1). Для построения данного фрактала достаточно напечатать в строке ввода «sierpinski gasket». Система не только показывает изображение после пяти итераций, но и наглядно демонстрирует алгоритм его получения, а также показывает размерность фрактала (~1,585; на рис.1 значение не отражено).
Фрактальная размерность временного ряда может находиться в пределах от 1 до 2. Фракталы могут описывать, например, временной ряд курса акций. Статистика временного ряда с фрактальными размерностями, отличными от 1,5, сильно отличается от гауссовой статистики и не обязательно подчиняется нормальному распределению. В частности, фрактальная природа рынка акций выражается в том, что кривые 1-, 5-, 10-, 20-, 30- и 90-дневных прибылей внешне выглядят одинаково (масштабно инвариантны) [2, 3]. Если мы не знаем, для какого периода времени построен график, мы не сможем это определить по его виду.
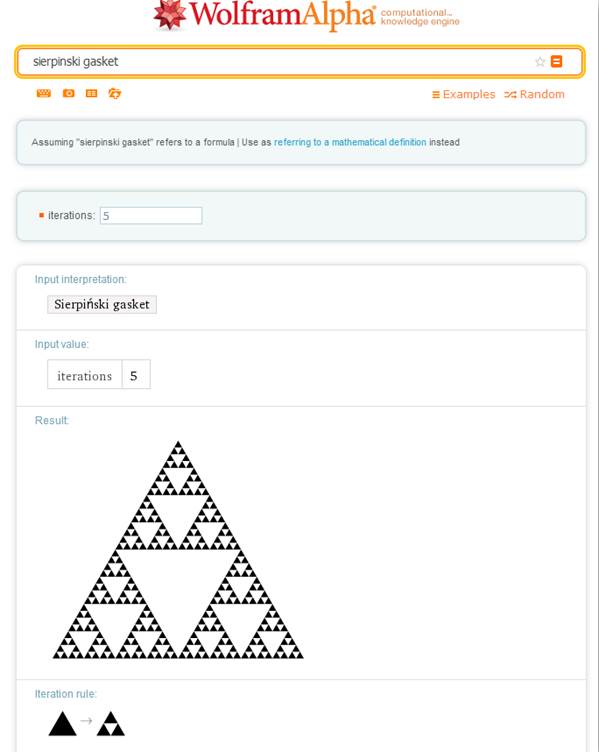
Рис. 1. Салфетка Серпинского
Фрактальность рынка также проявляется в том, что кривые распределения прибылей могут существенно отличаться от гауссовых (вероятность средних значений выше, чем для нормального распределения, и высока вероятность экстремально больших (более 3 сигм) отклонений). Это свойство также легко продемонстрировать в системе WolframAlpha. В настоящее время сервер использует мощные вычислительные ресурсы, интегрированные с множеством баз данных. В частности, можно получить сведения о динамике стоимости акций наиболее известных корпораций. Например, чтобы получить данные о корпорации Apple и узнать текущую стоимость ее акций, достаточно в строке вычислений ввести краткое название AAPL. Помимо различных сведений, важных для фундаментального анализа, можно увидеть графики изменения стоимости акций компании за различные периоды времени с кривыми гауссового приближения (рис. 2). Очевидно, что последние три графика достаточно далеки от графиков гауссового распределения.
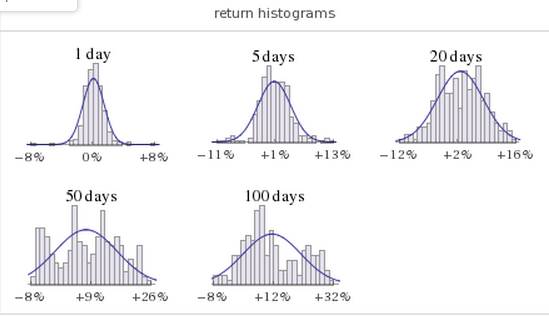
Рис. 2. Графики изменения стоимости акций компании Apple
Информативными являются также графики изменения стоимости акций за выбранный период времени. Так, можно наблюдать резкий рост стоимости акций компании после появления на рынке планшетных компьютеров. Кроме обычного вида графика можно «построить» график скользящей средней с различными интервалами сглаживания, а также получить данные в виде так называемых японских свечей.
В системе доступны также сведения о ряде российских компаний. Например, чтобы получить котировку акций Сбербанка, достаточно в строке вычислений ввести краткое название SBER (рис. 3). Из рис. 3 видно, что в настоящий момент стоимость одной акции Сбербанка составляет 491,11 рублей.
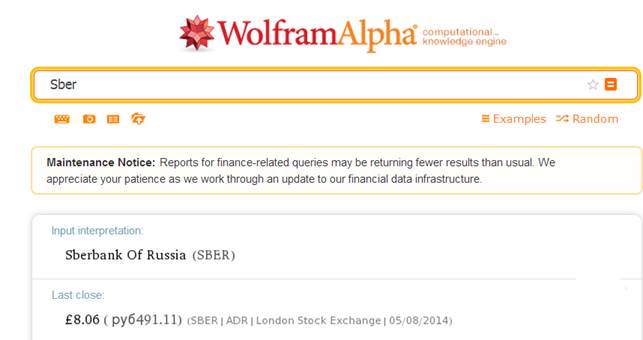
Рис. 3. Работа со строкой вычислений в системе WolframAlpha
Задачи теории графов
В курсе дискретной математики традиционно рассматривается такой раздел, как теория графов [1]. Строгое определение графа можно найти в учебниках по дискретной математике. Мы будем рассматривать граф как множество точек (называемых вершинами или узлами), соединенных между собой направленными или ненаправленными линиями (ребрами). С помощью графов часто оказывается удобным описывать многие системы (физические, технические, экономические, биологические, социальные и другие) и решать ряд задач (например, связанных с логистикой).
Чтобы задать граф в системе WolframAlpha, достаточно указать вершины, соединенные ребрами, например, 1®2, 2®1 и т.д.
Графы возникли в восемнадцатом столетии, когда известный математик Леонард Эйлер пытался решить теперь ставшую классическим примером задачу о Кенигсбергских мостах. В то время в городе Кенигсберге было два острова, соединенных семью мостами с берегами реки Преголь и друг с другом.
Задача, которую решал Эйлер, состоит в следующем: осуществить прогулку по городу таким образом, чтобы, пройдя ровно по одному разу по каждому мосту, вернуться в то же место, откуда начиналась прогулка. Решая эту задачу, Эйлер изобразил Кенигсберг в виде графа, отождествив его вершины с частями города, а ребра - с мостами, которыми связаны эти части. Эйлеру удалось показать, что решения задачи не существует.
Граф, для которого существует решение описанной выше задачи, называется эйлеровым. Чтобы выяснить в системе WolframAlpha, является ли граф эйлеровым, после задания графа необходимо написать eulerian cycle. В частности, граф задачи о Кенигсбергских мостах эйлеровым не является (рис. 4). В теории графов циклом называется замкнутый маршрут, все ребра которого различны. Эйлеров цикл - это цикл, который содержит все ребра графа, причем каждое ребро проходится ровно один раз.
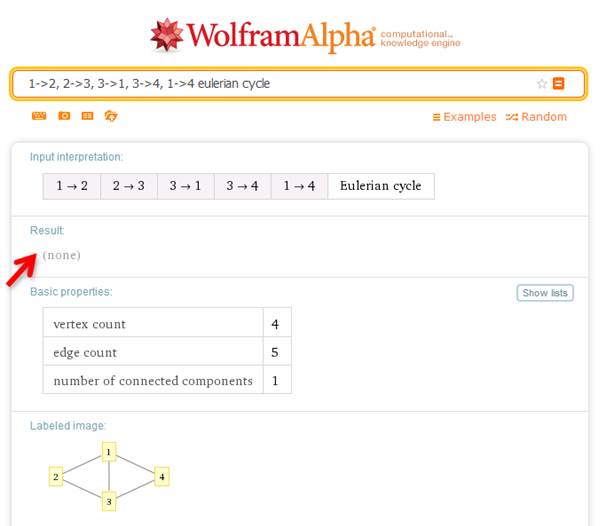
Рис. 4. Поиск эйлерова цикла в графе
Интересным случаем является также гамильтонов граф, содержащий гамильтонов цикл, в котором проходятся все вершины, причем каждая по одному разу. В отличие от эйлерова цикла, строгий математический критерий существования гамильтонова цикла в произвольном графе еще не найден. Решение этой проблемы имеет практическую ценность, так как оно связано с известной задачей о коммивояжере, который должен объехать несколько пунктов и вернуться обратно. Он обязан побывать в каждом пункте в точности по одному разу и заинтересован в том, чтобы затратить на поездку как можно меньше времени. Если при выполнении вычислений, показанных на рис. 3, вместо «eulerian cycle» написать «hamiltonian cycle», система даст ответ {1, 2, 3, 4,1}, что, очевидно, соответствует гамильтонову циклу данного графа.
Заключение
Облачные сервисы - это новый подход, предполагающий распределенную и удаленную обработку и хранение данных. В основе облачных вычислений выделяют такие особенности, как доступность через интернет, виртуализация, простота и стандартность. В данной работе мы рассматривали возможности облачного сервиса всемирно известной вычислительной системы Mathematica. «Облако» представляет собой крупный data-центр (или сеть взаимосвязанных между собой серверов), в котором хранятся файлы и совершаются все вычислительные операции. Это значит, что автоматически снимаются все проблемы, связанные с производительностью компьютера и количеством свободного места на винчестере. Все приведенные выше примеры можно реализовать даже на смартфоне или планшетном компьютере.
Одним из ключевых понятий сферы облачных технологий является Softwareas a Service (сокращенно - SaaS, т.е. ПО как сервис). Согласно SaaS-концепции вы как бы берете продукт в аренду, причем используете только те функции, которые вам нужны. Использование облачных вычислений также полностью снимает проблему компьютерного пиратства. Компьютерные программы достаточно дороги. Студенты и ВУЗы часто не в состоянии их купить. Используя технологию SaaS, вы получаете бесплатный или за небольшую плату онлайн-сервис, предоставляющий полные или ограниченные функциональные возможности программы. Среди наиболее известных современных систем вычислительной математики подобный сервис предлагают системы Mathematica и Mathcad.
Остановимся кратко на реализации облачных вычислений в Mathcad. Это сайт [6] Санкт-Петербургского политехнического университета (научный руководитель проекта - проф. Р.И. Ивановский) и расчетный сервер [4] НИУ МЭИ под научным руководством проф. В.Ф. Очкова. Основным достоинством системы Mathcad является реализация решений задач на естественном математическом языке с привлечением мощного математического аппарата (решение алгебраических и дифференциальных уравнений и систем, научная графика и анимация, статистика и т.п.). Расчеты, сделанные в среде Mathcad, можно публиковать в Интернете или Интранете для интерактивного использования по технологии MathcadCalculationServer (MCS). Хотя оба сервера принадлежат техническим ВУЗам, среди разработок достаточно много задач с экономическим содержанием. На этих сайтах можно найти не только справочно-информационные материалы в различном виде, но и «живые» расчеты, в которых можно изменить исходные данные и получить новый ответ.
В данной работе мы рассмотрели примеры применения облачного сервиса WolframAlpha в процессе преподавания математических курсов в экономическом ВУЗе, в частности, связанных с дискретной математикой, теорией графов, финансовыми вычислениями и т.п. Кроме упомянутых выше преимуществ предлагаемого нами подхода, следует отметить также повышение интереса студентов к изучению достаточно сложных дисциплин, использующих математические вычисления и экономико-математическое моделирование.
Рецензенты:
Черняев С.И., д.т.н., профессор кафедры «Промышленная экология и химия» Калужского филиала ФГБОУ ВПО «Московский государственный технический университет им. Н. Э. Баумана», г. Калуга.
Обрубов Ю.В., д.ф.-м.н., доцент кафедры «Высшая математика» Калужского филиала ФГБОУ ВПО «Московский государственный технический университет им. Н. Э. Баумана», г. Калуга.
Библиографическая ссылка
Князева И.В., Семененко М.Г., Кулакова Н.Н. ВНЕДРЕНИЕ ЭЛЕМЕНТОВ СОВРЕМЕННЫХ МАТЕМАТИЧЕСКИХ ИДЕЙ В ОБРАЗОВАТЕЛЬНЫЙ ПРОЦЕСС ЭКОНОМИЧЕСКОГО ВУЗА // Современные проблемы науки и образования. 2014. № 4. ;URL: https://science-education.ru/ru/article/view?id=14323 (дата обращения: 06.03.2026).



