В задачах автосервиса исходными предпосылками являются как качество ремонта каждого отдельного автомобиля, так и правильная организация всей ремонтной базы. Всегда нужно знать, какое количество авторемонтных мастерских или заводов нужно иметь для того, чтобы обеспечить своевременный ремонт автомашин. Если их будет мало, то возможно образование очереди автомобилей, ожидающих ремонта, которая может привести к большим материальным потерям: простои машин могут оказаться более дорогостоящими, чем расширение ремонтной базы. При этом неограниченное ее расширение не только неразумно, но и нереально: необходимо знать оптимальное решение, позволяющее решить задачу так, чтобы обеспечить минимальный простой автомашин в ожидании ремонта и расширить ремонтную базу без неоправданных финансовых издержек. Естественный путь решения задачи – итерационный, связанный с последовательной корректировкой принятых решений.
Определение оптимальной, в принятом смысле, организации функционирования обслуживающей системы одними качественными методами принципиально невозможно [4…6] и требует применения количественных методов решения (разработка математических методов; отыскание основных характеристик процессов обслуживания; оценка качества функционирования всей обслуживающей системы). Так, чтобы определить среднее число машин, нуждающихся в ремонте в данный момент, требуется установить число автомашин, выходящих из строя за определенный промежуток времени (зависит от времени года, от состояния дорог в данном районе, от квалификации водителей, соблюдения графиков профилактических осмотров и числа случайных факторов (нужно знать ее вероятностные характеристики)). Далее, как правило, нужно определить время ремонта (зависит от характера поломки или аварии, оснащенности ремонтной базы, опыта персонала по обслуживанию, наличия запасных частей и т.д.).
Знание потока требований (количество машин, нуждающихся в ремонте и осмотре) и времени обслуживания (ремонта) позволяет более строго решить задачу определения среднего числа автомашин, находящихся в ремонте.
Аналогичные задачи возникают и в деятельности транспортно-логистических компаний: оптимизация транспортных издержек и маршрутов перевозки грузов; расчет транспортных расходов; организация и обеспечение доставки товаров, экономическое обоснование вариантов доставки независимо от объема груза. Число заявок на обслуживание (перевозок грузов) может быть гораздо большим, чем могут обслужить все транспортные средства, принадлежащие конторе (ограничение приема заявок). Естественным ограничением является длина очереди (число заявок, ожидающих обслуживания). Если очередная заявка поступает в момент, когда очередь достигла определенной величины, она не принимается (отказ в обслуживании). При доставке срочных грузов заказчик не может ждать, пока его заявка может быть удовлетворена; заявка будет для конторы потеряна. Заказчик будет использовать другие возможности доставки своих грузов по назначению и в нужные сроки с привлечением других компаний. Существенным является определение вероятности того, что очередная заявка не будет принята на обслуживание. Задача усложняется тем, что время доставки грузов, заявки на перевозки которых поступили раньше, также является случайной величиной; указать точно, когда освободятся машины, заранее нельзя. Это время зависит от ряда факторов: откуда и куда нужно перевести грузы; какое время будет затрачено на погрузку и разгрузку (зависит от габаритов груза, тары, вида погрузки; от времени суток и времени года; от качества дороги; характера движения по дорогам и т.д.).
Для того чтобы предпринять какие-то конкретные шаги по реорганизации обслуживающей системы для улучшения качества ее функционирования, сначала следует изучить поток требований (с количественной оценкой), поступающих в эту систему, и определить требуемые математические методы [1…3].
Процесс поступления заявок на обслуживание есть случайный процесс: поток требований описывается случайной функцией ![]() (определяет число требований, нуждающихся в обслуживании за промежуток времени
(определяет число требований, нуждающихся в обслуживании за промежуток времени ![]() ; за данный промежуток времени
; за данный промежуток времени ![]() может и не поступить ни одного требования, а может поступить
может и не поступить ни одного требования, а может поступить ![]() требований; принимает только целочисленные значения).
требований; принимает только целочисленные значения).
Каждая реализация (число реализаций может быть бесконечным) случайной функции ![]() является неслучайной функцией одного аргумента времени; невозможно определить все ее реализации для полного описания. Поэтому используют другой способ ее задания. А именно: случайная функция
является неслучайной функцией одного аргумента времени; невозможно определить все ее реализации для полного описания. Поэтому используют другой способ ее задания. А именно: случайная функция ![]() будет полностью определена, если для любых положительных промежутков времени
будет полностью определена, если для любых положительных промежутков времени ![]() , можно указать число требований, поступивших за каждый из этих промежутков. Поток требований будет полностью описан, если будет известна вероятность
, можно указать число требований, поступивших за каждый из этих промежутков. Поток требований будет полностью описан, если будет известна вероятность ![]() для любой группы целых положительных чисел
для любой группы целых положительных чисел ![]() . Эта вероятность может быть отлична от нуля только тогда, если при
. Эта вероятность может быть отлична от нуля только тогда, если при ![]() величины
величины ![]() удовлетворяют условию
удовлетворяют условию ![]() (функция
(функция ![]() не убывает с возрастанием
не убывает с возрастанием ![]() ). Как видим, принципиально можно описать любой поток требований, но описание не всегда будет простым и достаточно удобным; изучение процесса массового обслуживания является далеко не тривиальной задачей. К счастью, на практике нередки потоки, обладающие свойствами, позволяющими найти более простые способы их описания. В частности, многие потоки требований обладают свойством стационарности (вероятность поступления заданного количества требований в течение определенного промежутка не зависит от начала отсчета времени, а зависит от длины промежутка). Поток будет стационарным, если закон распределения группы случайных величин
). Как видим, принципиально можно описать любой поток требований, но описание не всегда будет простым и достаточно удобным; изучение процесса массового обслуживания является далеко не тривиальной задачей. К счастью, на практике нередки потоки, обладающие свойствами, позволяющими найти более простые способы их описания. В частности, многие потоки требований обладают свойством стационарности (вероятность поступления заданного количества требований в течение определенного промежутка не зависит от начала отсчета времени, а зависит от длины промежутка). Поток будет стационарным, если закон распределения группы случайных величин ![]() совпадает с законом распределения
совпадает с законом распределения ![]() ; распределение случайных величин зависит от
; распределение случайных величин зависит от ![]() и не зависит от величины
и не зависит от величины ![]() (любой произвольный отрезок времени). Заметим, для стационарных потоков
(любой произвольный отрезок времени). Заметим, для стационарных потоков ![]() ;
; ![]() ; вероятность того, что ровно
; вероятность того, что ровно ![]() требований будет получено за промежуток времени
требований будет получено за промежуток времени ![]() , равна вероятности получения
, равна вероятности получения ![]() требований за промежуток времени
требований за промежуток времени ![]() .
.
Часто в реальных потоках число требований, поступивших в систему после произвольного момента времени ![]() , не зависит от того, какое число требований поступило в систему до момента
, не зависит от того, какое число требований поступило в систему до момента ![]() (отсутствие последействия). Известно [4…6], стационарный поток без последействия полностью характеризуется системой функций
(отсутствие последействия). Известно [4…6], стационарный поток без последействия полностью характеризуется системой функций ![]() ,
,![]() (вероятность того, что за промежуток времени
(вероятность того, что за промежуток времени ![]() при
при ![]() поступит точно
поступит точно ![]() требований).
требований).
При ординарном потоке (![]() или
или ![]() при
при ![]() , где
, где ![]() - вероятность появления за промежуток времени
- вероятность появления за промежуток времени ![]() не меньше двух требований) одновременное появление двух или большего числа требований считается невозможным; вероятность того, что появится больше одного требования за малый промежуток
не меньше двух требований) одновременное появление двух или большего числа требований считается невозможным; вероятность того, что появится больше одного требования за малый промежуток ![]() есть бесконечно малая величина более высокого порядка, чем
есть бесконечно малая величина более высокого порядка, чем ![]() .
.
Параметр стационарного потока (может быть неограниченно большой) есть ![]() или
или ![]() ;
; ![]() - вероятность того, что за время
- вероятность того, что за время ![]() поступит по крайней мере одно требование на обслуживание.
поступит по крайней мере одно требование на обслуживание.
Для стационарного ординарного потока с ограниченным последействием (обобщением простейшего потока) достаточно знания функции ![]() . Пальма (для простейшего потока - одной постоянной
. Пальма (для простейшего потока - одной постоянной ![]() ),
), ![]() - вероятность отсутствия требований за время
- вероятность отсутствия требований за время ![]() при условии, что за предшествующий промежуток времени
при условии, что за предшествующий промежуток времени ![]() поступило по крайней мере одно требование (
поступило по крайней мере одно требование (![]() - предшествующий
- предшествующий ![]() и смежный с ним промежуток времени);
и смежный с ним промежуток времени); ![]() - вероятность поступления по крайней мере одного требования за время
- вероятность поступления по крайней мере одного требования за время ![]() ;
; ![]() - условная вероятность отсутствия требований за время
- условная вероятность отсутствия требований за время ![]() при условии, что за промежуток времени
при условии, что за промежуток времени ![]() поступило хотя бы одно требование. Функция
поступило хотя бы одно требование. Функция ![]() равна вероятности того, что за время
равна вероятности того, что за время ![]() не поступит ни одного требования при условии, что в начальный момент поступило по крайней мере одно требование. Если
не поступит ни одного требования при условии, что в начальный момент поступило по крайней мере одно требование. Если ![]() есть начальный момент потока, а
есть начальный момент потока, а ![]() - моменты поступления последовательных требований, то
- моменты поступления последовательных требований, то ![]() так как
так как ![]() ,
, ![]() . Поток требований будет задан, если известны все моменты поступления требований или промежутки между смежными требованиями. Поскольку
. Поток требований будет задан, если известны все моменты поступления требований или промежутки между смежными требованиями. Поскольку ![]() - случайные величины, то для определения потока требований необходимо задать их закон распределения. Известно, для стационарного ординарного потока с ограниченным последействием функции распределения имеют вид:
- случайные величины, то для определения потока требований необходимо задать их закон распределения. Известно, для стационарного ординарного потока с ограниченным последействием функции распределения имеют вид:
![]()
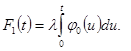
При ![]() стационарный ординарный поток с ограниченным последействием превращается в простейший поток.
стационарный ординарный поток с ограниченным последействием превращается в простейший поток.
Время обслуживания ![]() характеризует пропускную способность одного обслуживающего аппарата (не является оценкой качества обслуживания); является случайной величиной и может быть описано законом распределения
характеризует пропускную способность одного обслуживающего аппарата (не является оценкой качества обслуживания); является случайной величиной и может быть описано законом распределения ![]() ; обычно используется показательный закон распределения
; обычно используется показательный закон распределения ![]() ;
; ![]() . При показательном законе распределения времени обслуживания вероятность того, что обслуживание закончится вскоре после его начала велика. В реальных процессах обслуживания это свойство нередко не имеет места. Поэтому используются и другие законы распределения времени обслуживания (для решения задач массового обслуживания с любым законом распределения времени обслуживания можно воспользоваться методом Монте-Карло).
. При показательном законе распределения времени обслуживания вероятность того, что обслуживание закончится вскоре после его начала велика. В реальных процессах обслуживания это свойство нередко не имеет места. Поэтому используются и другие законы распределения времени обслуживания (для решения задач массового обслуживания с любым законом распределения времени обслуживания можно воспользоваться методом Монте-Карло).
Характер задач массового обслуживания во многом определяется структурой обслуживающей системы. Основные типы задач определяются характеризующими систему критериями. Выделяются системы обслуживания с потерями и без потерь. Нередко требование покидает систему и в других условиях (ограниченное время пребывания требования в системе обслуживания). Иногда используется ограничение времени ожидания начала обслуживания (смешанные системы обслуживания; требование покидает систему, если начало обслуживания превосходит определенную величину; если обслуживание начато, оно будет закончено независимо от того, какое время будет затрачено на обслуживание). Используются классификации обслуживающих систем с учетом ограниченности или неограниченности числа обслуживающих аппаратов или исходя от ограниченности или неограниченности потоков требований.
Укажем основные критерии эффективности для процессов массового обслуживания. Для систем с потерями важнейшей характеристикой является вероятность отказа в обслуживании (вероятность потери требования; вероятность отказа равна вероятности того, что все обслуживающие аппараты окажутся занятыми; степень загрузки обслуживающей системы определяется средним числом занятых аппаратов).
При оценке систем обслуживания без потерь в качестве критерия рассматривается длина очереди (случайная величина; определяется числом требований, ожидающих обслуживание; зависит от того, когда и сколько требований поступило в систему; сколько времени затрачено на обслуживание поступивших требований и т.д.). В качестве показателя длины очереди (критерий не является полным) часто используется ее математическое ожидание (характеризует потери из-за простаивания в очереди). С точки зрения обслуживания и чистых потерь за счет ожидания в очереди лучше использовать время ожидания начала обслуживания ![]() (случайная величина; зависит от количества требований, находящихся в данный момент в очереди, времени окончания обслуживания всех предыдущих требований и т.д.). Полной характеристикой времени ожидания будет закон распределения
(случайная величина; зависит от количества требований, находящихся в данный момент в очереди, времени окончания обслуживания всех предыдущих требований и т.д.). Полной характеристикой времени ожидания будет закон распределения ![]() (вероятность того, что обслуживание очередного времени будет начато немедленно, совпадает с вероятностью того, что в обслуживающейся системе есть хоть один свободный аппарат). Определение закона распределение не всегда просто. Поэтому используются более простые критерии: среднее время ожидания начала обслуживания, среднее число занятых обслуживающих аппаратов и др.
(вероятность того, что обслуживание очередного времени будет начато немедленно, совпадает с вероятностью того, что в обслуживающейся системе есть хоть один свободный аппарат). Определение закона распределение не всегда просто. Поэтому используются более простые критерии: среднее время ожидания начала обслуживания, среднее число занятых обслуживающих аппаратов и др.
Для обслуживающих систем смешанного типа от специфики условий каждой задачи могут появиться и свои специфические критерии. Так, в процессах обслуживания, в которых требование не может находиться в обслуживающей системе больше заданного времени и покидает ее, используется время, затраченное на обслуживание тех требований, которые покинут систему до окончания обслуживания. Требование покидает систему, когда его обслуживание закончено или истекло допустимое время пребывания в системе, а также в случае, когда обслуживание требования или не начато совсем, или произведено частично (непроизводительные затраты). Часто в качестве критерия используется время, затраченное каждым аппаратом на обслуживание таких требований, и суммарное время, затраченное всеми аппаратами системы.
Анализировалась работа автотранспортной компании, имеющей в своем распоряжении 5 автомашин и обеспечивающей круглосуточную срочную доставку грузов (при ограниченном числе заявок на доставку; отказ в обслуживании при количестве заявок >10 (максимальная длина очереди – 10; прием заявок прекращается, пока не будет обслужена одна очередная заявка и очередь уменьшится)). Поток заявок предполагается простейшим, среднее количество заявок в час ![]() . Вероятность поступления ровно
. Вероятность поступления ровно ![]() заявок за время
заявок за время ![]() :
: ![]() При показательном законе распределения времени доставки груза (время обслуживания; зависит: от того, где находится груз, куда его необходимо доставить, вида груза, времени суток, качества дороги и т.д.) параметр
При показательном законе распределения времени доставки груза (время обслуживания; зависит: от того, где находится груз, куда его необходимо доставить, вида груза, времени суток, качества дороги и т.д.) параметр ![]() будет равен единице, если на удовлетворение одной заявки требуется один час.
будет равен единице, если на удовлетворение одной заявки требуется один час.
Определим показатели работы компании (вероятность того, что все машины заняты; среднюю длину очереди и др.). Здесь требованием на обслуживание является заявка на доставку груза; обслуживающий аппарат - автомашина; обслуживание – доставка груза; число обслуживающих аппаратов системы (компании) ![]() , максимальная длина очереди
, максимальная длина очереди ![]() ; наибольшее число заявок обслуживаемых и ожидающих обслуживания
; наибольшее число заявок обслуживаемых и ожидающих обслуживания ![]() . Вероятность того, что все машины заняты, есть
. Вероятность того, что все машины заняты, есть 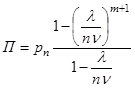 ;
;
![]() - вероятность того, что занято точно
- вероятность того, что занято точно ![]() обслуживающих аппаратов при условии, что общее число требований, находящихся на обслуживании не превосходит числа обслуживающих аппаратов, определяется (при
обслуживающих аппаратов при условии, что общее число требований, находящихся на обслуживании не превосходит числа обслуживающих аппаратов, определяется (при ![]() ) в соответствии с
) в соответствии с 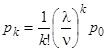 ,
, ![]() ;
; ![]() - среднее число требований, поступающих в систему за единицу времени;
- среднее число требований, поступающих в систему за единицу времени; ![]() - среднее время обслуживания одной автомашиной одного требования;
- среднее время обслуживания одной автомашиной одного требования; ![]() - вероятность того, что все обслуживающие машины свободны,
- вероятность того, что все обслуживающие машины свободны, 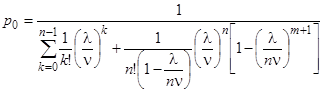 ;
; ![]() - наибольшая допустимая длина очереди;
- наибольшая допустимая длина очереди; ![]() - число обслуживающих автомашин.
- число обслуживающих автомашин.
С учетом ![]() ,
, ![]() получим
получим
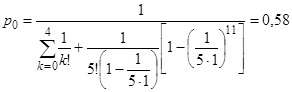 ;
; 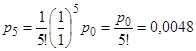 .
.
Имеем ![]() ; вероятность полной загруженности компании мала.
; вероятность полной загруженности компании мала.
Качество обслуживания определится средней длиной очереди (среднее число требований, ожидающих начало обслуживания)
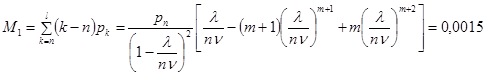 ;
;
практически очереди не будет.
Таким образом, при выбранных значениях (![]() ,
,![]() ,
,![]() ) заказчик практически не получит отказа в обслуживании, однако и загрузка машин будет незначительна (задаваясь иными значениями
) заказчик практически не получит отказа в обслуживании, однако и загрузка машин будет незначительна (задаваясь иными значениями ![]() ,
,![]() ,
,![]() , можно скорректировать работу компании в необходимом направлении).
, можно скорректировать работу компании в необходимом направлении).
Рецензенты:
Родионов Ю.В., д.т.н., профессор, директор Автомобильно-дорожного института ПГУАС, профессор кафедры «Эксплуатация автомобильного транспорта», г. Пенза.
Логанина В.И., д.т.н., профессор, зав. кафедрой «Управление качеством и технологии строительного производства» ПГУАС, г. Пенза.
Библиографическая ссылка
Гарькина И.А., Данилов А.М., Карев М.Н. АВТОСЕРВИС И ПЕРЕВОЗКИ С ПОЗИЦИЙ ТЕОРИИ СИСТЕМ МАССОВОГО ОБСЛУЖИВАНИЯ // Современные проблемы науки и образования. 2014. № 4. ;URL: https://science-education.ru/ru/article/view?id=14281 (дата обращения: 06.03.2026).



