На основании Распоряжения от 14 февраля 2008 г. N 300р об утверждении стандарта ОАО "РЖД" в локомотивных депо Октябрьской железной дороги проводится техническая учеба сотрудников. При этом в соответствии с Указанием Т-17/у от 22 апреля 2011 г. разрешено проведение технический занятий с использованием системы дистанционного обучения (СДО) на базе ЦИИТО (Центра интернет/интранет технологий в обучении) ФГБОУ ВПО ПГУПС. Каждый сотрудник имеет доступ к учебным материалам через сети передачи данных ОАО «РЖД» и/или Интернет, что позволяет ему проходить обучение в удобное для него время и в удобном месте.
Сотрудникам локомотивных бригад необходимо присутствовать на технических занятиях несколько раз в месяц и проходить тестирование по итогам этих занятий. При этом важной является задача анализа и оценивания результатов обучения. Это связано как с организационными проблемами, так и с экономическими, поскольку сотрудники, успешно завершившие изучение месячных тем, получают денежное вознаграждение.
Машинисты локомотивов имеют возможность повысить уровень своей заработной платы при условии повышения класса. На основании приказа 23Ц «О порядке проведения испытаний, выдачи свидетельств на право управления локомотивом, моторвагонным подвижным составом на путях общего пользования и присвоения класса квалификации машинистам локомотивов и моторвагонного подвижного состава» от 11 ноября 1997 г. для получения нового класса необходимо провести проверку знаний законодательства Российской Федерации, приказов, указаний, инструкций и иных актов МПС России, а также проверку знаний о порядке действий в нестандартных ситуациях. В процессе обучения с использованием СДО проверка знаний осуществляется постоянно.
В работе [5] был проведен анализ и оценка проходного балла тестирования. Однако, данный метод не учитывал то, что вопросы могут быть неравнозначными. Одним из способов решения этой проблемы является оценка значимости вопросов с помощью экспертной группы. Однако, такой способ требует существенных финансовых и организационных затрат и является фактически неприменимым на практике.
С другой стороны, мы имеем большой банк данных результатов тестирования машинистов, имеющих большой опыт работы. Качество их ответов позволит придать вопросам соответствующие веса, определяющие их значимость. Предлагаемый метод использует эти данные в качестве эталона для проведения оценки результатов тестирования претендентов на повышение класса.
В данной работе предлагается построение математической модели оценивания результатов тестирования, использующей дискриминантный анализ – метод классификации многомерных наблюдений в ситуации, когда имеется несколько обучающих выборок данных.
Первой выборкой является набор результатов тестирования машинистов, которые рассматриваются как эксперты. Второй выборкой – набор результатов помощников машинистов, заведомо не прошедших тестирование. Поскольку в работе [5] был получен проходной балл в интервале от 70% до 80%, то в качестве верхнего порогового значения нами выбран средний балл в 60%. Для помощников, набравших средний балл более 60%, проведем более детальный анализ, используя упомянутый выше дискриминантный метод многомерной классификации.
Использование дистанционного обучения при проведении технических занятий позволяет использовать достаточно широкий функционал современных информационных технологий. Тестирование, проводимое при помощи СДО, дает возможность хранить результаты тестирования всех сотрудников, а также проводить анализ полученных результатов. Кроме того существует возможность дифференцирования полученных ответов на основе должности сотрудника.
В качестве результатов тестирования рассматриваются результаты проведенного теста по одной из основных инструкций на железном транспорте – «Инструкция по движению поездов и маневровой работе на железнодорожном транспорте РФ - Приложение №8 к приказу Минтранса России от 04.06.2012г. №162». В результате исследования были получены две обучающие выборки, построенные по одному и тому же набору вопросов.
Задача дискриминантного анализа относится к разделу многомерного статистического анализа. Она представляет собой задачу классификации многомерных наблюдений в случае, когда имеются так называемые обучающие выборки.
В общем виде задача формулируется следующим образом.
Пусть имеется 2 совокупности ![]() и
и ![]() каждая из которых содержит
каждая из которых содержит ![]() k-мерных наблюдений
k-мерных наблюдений ![]() ,
, ![]() Пусть вероятность того, что наблюдение ведется над индивидуумом из генеральной совокупности
Пусть вероятность того, что наблюдение ведется над индивидуумом из генеральной совокупности ![]() равна α, тогда соответствующая вероятность для генеральной совокупности
равна α, тогда соответствующая вероятность для генеральной совокупности ![]() – (1-α).
– (1-α).
Новым наблюдением является k-мерный вектор ![]() Необходимо установить правило, по которому этот вектор будет отнесен к одной из возможных совокупностей
Необходимо установить правило, по которому этот вектор будет отнесен к одной из возможных совокупностей ![]() или
или ![]()
В нашем случае обучающими выборками являются:
![]() Результаты тестирования машинистов.
Результаты тестирования машинистов.
![]() Результаты тестирования помощников машинистов, набравших средний балл 60% и ниже.
Результаты тестирования помощников машинистов, набравших средний балл 60% и ниже.
Требуется принять решение по данному результату (при сдаче новым сотрудником) для помощника машиниста, считать ли прохождение теста успешным (будет ли отнесен результат к совокупности ![]() ).
).
Для решения поставленной задачи используем байесовский подход.
В случае, когда распределения вероятностей обучающих выборок известны, и плотности распределений равны ![]() и
и ![]() соответственно, критерий принятия решения выглядит следующим образом.
соответственно, критерий принятия решения выглядит следующим образом.
Область значений ![]() вектора Y разбивается на две части
вектора Y разбивается на две части ![]() , определяемые как
, определяемые как
![]() ,
,
![]() . (1)
. (1)
В случае, если наблюдение ![]() , отнесем его к совокупности
, отнесем его к совокупности ![]() , иначе - к совокупности
, иначе - к совокупности ![]() .
.
В задаче тестирования априорные вероятности неизвестны. Однако и в этом случае, метод Байеса является допустимым, т.е. таким, который нельзя улучшить.
Экспериментальное исследование
Для теста, состоящего из 10 вопросов, выбранных из общего пула, были собраны результаты ответов машинистов и помощников, затем была проведена сравнительная оценка вероятностей правильных ответов на вопросы для этих двух групп. Полученные результаты приведены на рис.1. По диаграмме видно, что не все машинисты дают 100% ответы на вопросы, что позволяет на основе эмпирических данных судить о значимости каждого из вопросов теста для экспертной группы.
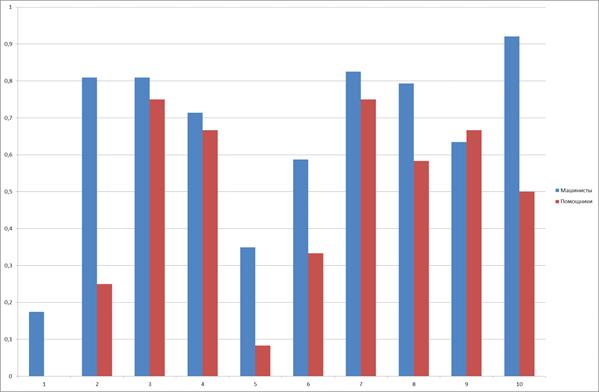
Рис.1. Сравнение оценок вероятностей получения верных ответов
В данном случае результаты тестирования являются случайными величинами дискретного типа, следовательно, вместо плотностей будем рассматривать распределения ![]() и
и![]() . В ходе анализа будем считать выбранные вопросы тестирования независимыми между собой. Тогда каждое наблюдение состоит из 10 независимых случайных величин, имеющих распределение Бернулли таких, что
. В ходе анализа будем считать выбранные вопросы тестирования независимыми между собой. Тогда каждое наблюдение состоит из 10 независимых случайных величин, имеющих распределение Бернулли таких, что
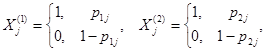
![]()
Вероятности правильных ответов ![]() оцениваются по имеющимся выборкам данных.
оцениваются по имеющимся выборкам данных.
Заметим, что никто из помощников машинистов не дал правильного ответа на первый вопрос, что дало ![]() . Для проведения дальнейшего анализа подправим полученное нулевое значение вероятности, заменив его на малое значение
. Для проведения дальнейшего анализа подправим полученное нулевое значение вероятности, заменив его на малое значение ![]() . Тогда эмпирически оцененные распределения
. Тогда эмпирически оцененные распределения ![]() и
и ![]() будут иметь вид
будут иметь вид
![]() ,
, 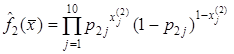 .
.
Используя критерий (1), отнесем наблюдение к соответствующей совокупности. Поскольку у нас не имеется никаких априорных условий, позволяющих отнести нового претендента к одной из групп, положим в критерии (1) значение ![]() .
.
Проведя анализ результатов тестирования помощников машинистов, мы увидели в частности, что часть результатов со средним баллом 70% являются более близкими к эталонной группе и данные результаты теста приняты нашим методом как успешные. Тогда как другие результаты с тем же баллом были признаны неуспешными. Проведя оценку ошибки дискриминации с помощью следующей формулы
![]()
мы получили, что она составляет 6%.
В заключении заметим, что хотя в исследовании были рассмотрены выборки результатов тестов, состоящих только из 10 вопросов, метод может применяться для тестовых блоков любой длины.
Рецензенты:
Боровских Ю.В., д.ф.-м.н., профессор кафедры «Математика и моделирование», ФГБОУ ВПО Петербургский государственный университет путей сообщения Императора Александра I, г.Санкт-Петербург.
Грибкова Н.В., д.ф.-м.н., профессор кафедры «Математика и моделирование», ФГБОУ ВПО Петербургский государственный университет путей сообщения Императора Александра I, г.Санкт-Петербург.
Библиографическая ссылка
Седов М.С., Гадасина Л.В., Куранова О.Н. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ОЦЕНИВАНИЯ РЕЗУЛЬТАТОВ ТЕСТИРОВАНИЯ ЛОКОМОТИВНЫХ БРИГАД ДИРЕКЦИИ ТЯГИ ОКТЯБРЬСКОЙ ЖЕЛЕЗНОЙ ДОРОГИ ФИЛИАЛА ОАО «РЖД» // Современные проблемы науки и образования. 2014. № 4. ;URL: https://science-education.ru/ru/article/view?id=14139 (дата обращения: 06.03.2026).



