При решении задачи синтеза управления необходимо найти математическое выражение, которое описывает функциональную зависимость управления от координат пространства состояния объекта управления. Найденная функция должна для любого начального состояния объекта из некоторой заданной области находить управление, которое обеспечит достижение цели управления с оптимальным значением заданного критерия качества. В последнее время задачу синтеза системы управления стало возможным решать с помощью методов символьной регрессии [5,6,8]. Мы применяем для решения задачи синтеза управления метод сетевого оператора [1-4], который представляет математическое выражение в форме целочисленной матрицы. Одним из преимуществ метода сетевого оператора перед другими методами является использование принципа базисного решения. Согласно этому принципу множество возможных решений задается в виде одного базисного решения и множества его малых вариаций. Эволюционные преобразования множества возможных решений и поиск оптимального решения осуществляются на множестве малых вариаций базисного решения. Успешность задания базисного решения определяет скорость сходимости алгоритма поиска. Решение задачи синтеза управления имеет смысл только для множества начальных состояний объекта управления, потому что найденная синтезирующая функция описывает зависимость управления от состояния объекта. Для того, чтобы решить эту проблему, метод сетевого оператора оценивает каждое возможное решение по выполнению терминальных условий и значениям критерия качества для множества начальных состояний объекта.
В настоящей работе мы применяем метод сетевого оператора для решения задачи синтеза системы управления группой объектов. Мы рассматриваем группу объектов как один объект управления с расширенными векторами состояния и управления. Такой подход, когда каждый объект в группе объектов является самостоятельной единицей, имеющей полное знание о состоянии других объектов в группе, является на наш взгляд перспективным в виду высокого развития современных технологий и удешевления комплектующих, которые еще недавно стоили дорого.
Дополнительным ограничением задачи являются динамические ограничения, определяющие отсутствие столкновений объектов с учетом их габаритов во время процесса управления. Мы применили метод сетевого оператора для решения задачи управления двумя мобильными роботами. Метод позволил найти синтезирующую функцию, которая обеспечивает достижение цели каждым объектом, при этом удовлетворено условие отсутствия столкновений роботов и обеспечена хорошая оценка качества управления.
Задача синтеза управления группой объектов
Заданы модели 
объектов управления
, 
, (1)
где 
- вектор состояния объекта 
, 
- вектор управления объекта , 
, 
, 
, 
- компактные множества в соответствующих векторных пространствах 
, .
Заданы области начальных значений
, , (2)
Заданы терминальные условия
, 
, . (3)
где 
, 
- максимальная длительность процесса управления.
Заданы кинематические уравнения, описывающие положения габаритных точек объектов
, , (4)
где 
, .
Заданы ограничения
, 
, 
, (5)
где 
.
Выполнение условия (5) определяет отсутствие столкновения между объектами и 
.
Заданы функционалы качества
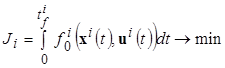, , (6)
где 
- ограниченные снизу непрерывные функции, 
.
Необходимо найти синтезирующую функцию управления в виде
, (7)
где 
.
Синтезирующая функция (7) должна обеспечивать достижение системой (1) такого целевого состояния
, , (8)
, , 
, 
, при котором выполняются условия (3) - (5) и обеспечивается минимум функционала (6).
Для решения задачи используем численный метод сетевого оператора.
Метод сетевого оператора
Подробно метод сетевого оператора описан в работах [1–4]. Применение метода сетевого оператора не предполагает никаких аналитических преобразований исходной постановки задачи. Единственным изменением задачи является замена множества начальных значений конечным множеством точек начальных значений:
, , (9)
Проверка терминальных условий (3), ограничений (5) и вычисление критерия качества (6) выполняется для каждого начального значения из (9) и терминальных условий. Окончательная оценка возможного решения определяется по сумме значений функционалов (6) для всех начальных значений из (9) с учетом штрафа за нарушение ограничений (5) и промаха при выполнении терминальных условий (3).
Сетевой оператор является структурой данных, которая позволяет описывать математические выражения в форме целочисленной матрицы.
Для организации поиска решения метод сетевого оператора использует принцип вариаций базисного решения. Метод использует четыре малые вариации, такие как замена унарной операции, замена бинарной операции, добавление унарной операции, удаление унарной операции.
Для представления вариаций используем вектор из четырех компонент
, (10)
где 
- номер малой вариации, 
, 
- номер строки и столбца, 
- номер унарной или бинарной операции.
Для реализации поиска оптимального сетевого оператора 
используется упорядоченное множество элементарных вариаций
, (11)
.
Поиск начинаем с сетевого оператора 
, который определяется исследователем по принципу максимальной близости к желаемому решению. Такой сетевой оператор называем базовым сетевым оператором.
Далее формируем множество вариаций 
, 
, и вычисляем значения целевых функций для каждого нового сетевого оператора 
.
В случае, если мы находим сетевой оператор, имеющий значение целевой функции лучшее, чем у базового сетевого оператора, тогда производим замену базового сетевого оператора на новый найденный сетевой оператор.
Для поиска можно использовать любой эволюционный алгоритм. В наших исследованиях мы использовали генетический алгоритм, который осуществлял поиск оптимального решения с помощью генетических операторов скрещивания и мутации над упорядоченными множествами элементарных вариаций (12).
Пример
В качестве примера рассмотрим синтез системы управления группой из двух мобильных роботов.
Математическая модель объектов управления имеет следующий вид [7]:
,
,
,
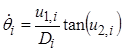где 
, 
- координаты центра масс, 
- угол, образуемый вектором скорости, 
- общий геометрический параметр робота .
Заданы начальные условия
, 
Заданы терминальные условия
, 
, 
.
Заданы ограничения на управления
, 
.
Мобильный робот представляет собой прямоугольник. Координаты углов робота определяем из соотношений
,
,
где - номер угла робота, 
.
,
,
,
,
,
,
,
.
Условие столкновения угла 
, 
, робота с роботом , , определяем из соотношений
,
,
где
,
,
,
.
Аналогично определяются условия столкновения угла , , робота с роботом , , определяем из соотношений
,
.
При выполнении условий столкновения углом робота с роботом определяем величину штрафа
,
,
.
В отсутствии столкновения штраф равнялся нулю.
Критерием качества управления являлось суммарное время попадания в терминальные условия с учетом штрафов за столкновения и точности попадания по всем начальным значениям.
При поиске решения использовали следующие параметры модели. Число роботов 
. Параметр размера робота 
. Начальные условия 
, 
, 
, 
, 
, 
, 
, 
, , 
, 
, .
Терминальные условия: 
, 
, 
, 
, 
, 
.
Ограничения на управление: 
, 
, 
, 
, 
, 
, 
, 
.
При вычислениях был использован генетический алгоритм со следующими значениями параметров: мощность начального множества возможных решений 1024, число поколений 128, число скрещиваемых пар в одном поколении 128, число векторов вариаций для одного решения 12, число поколений между сменой базисного решения 24, вероятность мутации 0.7, размерность матрицы сетевого оператора 
.
Первоначально для управления было задано тривиальное базисное решение в виде
,
,
.
,
где 
, 
.
Вместе с поиском структуры методом сетевого оператора этим же генетическим алгоритмом искали значения параметров 
,…, 
. Для алгоритма поиска параметров было задано 4 бита для целой части числа и 12 бит для дробной части числа.
При поиске решения было сделано около 10 запусков. Каждый запуск использовал новое базисное решение, которое было отобрано как наилучшее решение на предыдущем запуске. Время вычисления, затраченное на один запуск, составляло 35 мин. Вычисления выполнялись на компьютере с процессором Intel(R) Core(TM) i7-2640M CPU @ 2.80GHz 2.80 GHz.
В результате вычислений было получено следующее решение
, 
,
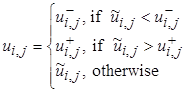где
,
,
,
,
,
,
, 
, 
,
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
.
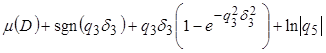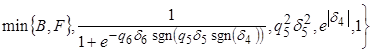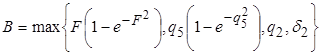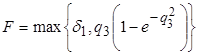Сложное математическое выражение для синтезирующей функции управления получено из найденной оптимальной матрицы сетевого оператора.
Согласно условию задачи синтезирующая функция должна обеспечивать получения управления, которое переместит двух роботов из двух различных начальных положений в одно терминальное положение. Начальные состояния были заданы так, что при движении роботов их первого начального состояния в терминальное положение должны пересекаться (см. Рис. 2).
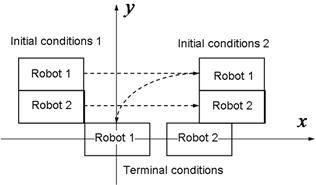
Рис.2. Начальные и конечные состояния роботов
Найденная синтезирующая функция обеспечивает такое управления, при котором оба робота их первого начального состояния перемещаются во второе состояния, а затем без пересечения траекторий перемещаются в терминальное состояние.
Результаты моделирования полученной системы управления сразу для двух начальных условий приведены на рис. 3.
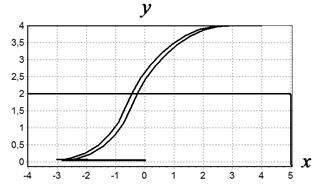
Рис.3. Траектории движения роботов из разных начальных условий
Работа выполнена при поддержке фонда РФФИ 13-08-00523-a and 14-08-00008-a.
Рецензенты:
Юрков Н.К., д.т.н., профессор, зав.кафедрой «Конструирование и производство радиоаппаратуры» ФГБОУ ВПО «Пензенский государственный университет», г.Пенза.
Никульчев Е.В., д.т.н., профессор, проректор по научной работе НОУ ВПО Московский технологический институт "ВТУ", г.Москва.
Библиографическая ссылка
Дивеев А.И., Шмалько Е.Ю. СИНТЕЗ СИСТЕМЫ УПРАВЛЕНИЯ ГРУППОЙ РОБОТОВ МЕТОДОМ СЕТЕВОГО ОПЕРАТОРА // Современные проблемы науки и образования. – 2014. – № 4. ;URL: https://science-education.ru/ru/article/view?id=14123 (дата обращения: 21.11.2024).