В задачах радиоастрономии и дистанционного зондирования поверхности решающую роль играет оптимальная или близкая к ней обработка полученных данных с тем, чтобы реализовать эффективное решение проблемы определения класса наблюдаемого сигнала. Эффективное решение проблемы определения класса [3-6] может быть получено в рамках классической теории многоальтернативной проверки статистических гипотез. По одной из них вектор принимаемых колебаний ![]() порожден только шумом. Остальные гипотезы соответствуют наблюдению различных классов сигналов. Общее число возможных классов –М, число гипотез – (М+1).
порожден только шумом. Остальные гипотезы соответствуют наблюдению различных классов сигналов. Общее число возможных классов –М, число гипотез – (М+1).
Классическое решение задачи многоальтернативной проверки гипотез приводит к структуре устройства обработки принимаемых сигналов, состоящей из М параллельных каналов формирования отношения правдоподобия или его логарифма
![]() ,
,
и решающего устройства, на М входов которого поступают значения lk. Решающее устройство выносит решение в пользу одного из М сигналов. Способ принятия решения зависит от выбранного критерия качества. При использовании критерия максимального правдоподобия решение выносится в пользу гипотезы с максимальным значением lk. В любом случае наибольший практический интерес представляет процедура формирования отношения правдоподобия и структурная схема устройства, реализующего это отношение.
Достаточная статистика для принятия решения представляет собой вектор, составленный из отношений правдоподобия для каждой из М конкурирующих гипотез. Логарифм отношения правдоподобия для k-й гипотезы может быть записан в виде:
![]()
![]() (1)
(1)
где K0 и Kk – нормирующие коэффициенты функционалов плотности распределения вероятностей для случаев наблюдения только шума и k-го сигнала на фоне шума; Q0(t,u), Qk(t,u) – комплексные матрицы, обратные матрицам взаимной корреляции принимаемого вектора ![]() для гипотез о наблюдении только шума R(t,u) и k-го сигнала на фоне шума Rk(t,u).
для гипотез о наблюдении только шума R(t,u) и k-го сигнала на фоне шума Rk(t,u).
Поскольку шум и диффузионная составляющая принимаемого сигнала ![]() являются независимыми случайными процессами, то
являются независимыми случайными процессами, то
![]() , (2)
, (2)
где
![]() (3)
(3)
– матрица корреляционных функций диффузионных составляющих вектора принимаемого сигнала.
Для определения вида матриц Q0(t,u) и Qk(t,u) следует воспользоваться интегрально-матричными уравнениями обращения [1]:
![]() ; (4)
; (4)
![]() , (5)
, (5)
где I– единичная диагональная матрица.
Для последнего слагаемого в (1) справедливо равенство [2]:
![]() , (6)
, (6)
где QAk (u,t) – решение интегрально-матричного уравнения:
![]() (7)
(7)
При условии, что шум «белый» с диагональной матрицей спектральных плотностей N0 выражения (4–7) упрощаются:
![]() , (8)
, (8)
![]() (9)
(9)
![]() , (10)
, (10)
![]() . (11)
. (11)
Пользуясь рекомендациями [1], ищем матрицу Qk(t,u) в виде
![]() , (12)
, (12)
В этом случае равенство (9) преобразуется следующим образом:
![]() . (13)
. (13)
Сравнение (11) с (13) показывает, что матрица Qk0(t,u) может быть найдена путем решения (11) при А = 1, т.е.
![]() . (14)
. (14)
Подставляя (8) в (1), получим:
![]()
![]() (15)
(15)
Последнее выражение позволяет представить один из возможных вариантов структуры устройства формирования логарифма отношения правдоподобия для k-й гипотезы (рис. 1). Из (15) и рис. 1 следует, что основу устройства формирования ![]() составляют два корреляционных канала. В одном из них вычисляется корреляция принимаемой реализации вектора
составляют два корреляционных канала. В одном из них вычисляется корреляция принимаемой реализации вектора ![]() , нормированного к мощности шумов, с вектором ожидаемого сигнала, порожденного отдельными детерминированными составляющими сигнала k-го класса
, нормированного к мощности шумов, с вектором ожидаемого сигнала, порожденного отдельными детерминированными составляющими сигнала k-го класса![]() . Во втором канале разностный сигнал
. Во втором канале разностный сигнал ![]() коррелируется с вектором
коррелируется с вектором
![]() ,
,
который представляет собой оценку диффузионной составляющей принимаемого сигнала в предположении о наблюдении сигнала k-го класса.
По существу в работе предложен оценочно-корреляционный алгоритм формирования отношения правдоподобия, другими словами, вектора достаточных статистик для принятия решения о классах наблюдаемых сигналов.
Названный алгоритм обеспечивает оптимальный приём и обработку флуктуирующего сигнала при наличии искажений и помех.
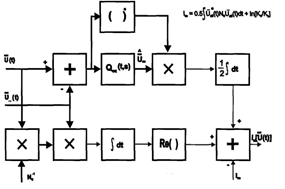
Рис. 1. Структурная схема формирования логарифма отношения правдоподобия
Потенциальные возможности решения задачи распознавания в подавляющем большинстве практических случаев характеризуются вероятностями вынесения правильных (Рпр) и ошибочных (Рош) решений. Точный аналитический расчет этих вероятностей может быть выполнен лишь в простейших частных случаях. В этих условиях для получения количественных оценок вероятностных характеристик работы системы наиболее целесообразным следует признать использование граничных соотношений Кайлата [7], которые были введены для случая проверки двух гипотез и в данной работе распространены на произвольное их количество.
При проверке (М+1) гипотез вероятность вынесения ошибочного решения равна:
![]() (16)
(16)
где рi – априорная вероятность i-й гипотезы,
p(j/i) – вероятность вынесения решения в пользу j-й гипотезы в том случае, когда истинной является 1-я гипотеза.
Это выражение можно представить в виде:
![]() (17)
(17)
В дальнейшем предполагаем, что решение в пользу того или иного класса принимается с использованием критерия минимума полной вероятности ошибки.
Используя методику [1], можно найти верхнюю границу ошибки (17) при проверке многих гипотез:
![]() (18)
(18)
В последнем выражении ChFij и ChMij – границы Чернова для вероятностей ложной тревоги и пропуска цели при проверке пары гипотез i и j независимо от остальных гипотез.
Необходимо отметить, что оценка ошибки, даваемая неравенством (18), может быть существенно завышена, причем точность оценки в общем случае уменьшается по мере увеличения числа конкурирующих гипотез.
В этих условиях представляется безусловно целесообразным нахождение и нижней границы вероятности ошибки правильной классификации (16). Для бинарного обнаружения такая граница введена Кайлатом [7]. В данной работе произведено обобщение названной границы на случай произвольного числа гипотез.
Для отыскания нижней границы вероятности ошибки воспользуемся выражением (16). Сумма по j в его правой части представляет собой вероятность вынесения ошибочного решения при наблюдении цели i-го класса. Такая ошибка возникает, если хотя бы для одной из альтернативных гипотез выполняется неравенство:
![]() (19)
(19)
в котором ![]() (20)
(20)
- логарифм отношения правдоподобия при проверке пары гипотез с номерами j и i; Wj(U) и Wi(U) – плотности распределения вероятностей значений вектора наблюдаемых данных U по гипотезам j и i. Пусть событие Аj соответствует выполнению условия (19). Тогда вероятность ошибки при наблюдении i-го класса целей представляется как вероятность суммы событий:

Используя формулу для определения вероятности суммы зависимых событий, можно убедиться в справедливости неравенства:
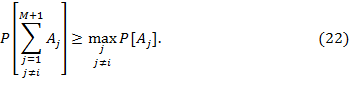
В этом выражении р[Aj] представляет собой вероятность вынесения решения в пользу j-гo класса целей при условии, что истинной является цель i-го класса при проверке только этой пары альтернатив. Обозначая эту вероятность P2(j/i) и используя (22), для вероятности ошибки (16) запишем неравенство:

где на значение j наложено единственное ограничение:
j ≠ i. (24)
Неравенство (23) позволяет оценить нижнюю границу вероятности ошибки в случае проверки более двух гипотез. Поскольку нас, в первую очередь, интересует случай распознавания трех классов, сосредоточим внимание именно на этой задаче (обобщение на произвольное число классов производится аналогично).
Используя (22) и (23), запишем два очевидных неравенства:
![]() (2/1)
(2/1)![]() (3/2)
(3/2)![]() (1/3)
(1/3)![]()
![]() (3/1)
(3/1)![]() (1/2)
(1/2)![]() (2/3)
(2/3)![]() (25)
(25)
Суммируя правые и левые части этих неравенств, получим:
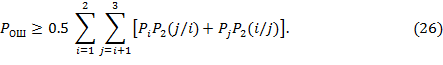
Выражение, стоящее в квадратных скобках (26), представляет собой вероятность ошибки при решении задачи проверки двух гипотез – i-й и j-й. Для оценки этой ошибки воспользуемся методикой, предложенной в [1]. При этом необходимо помнить, что в нашей постановке гипотезы с номерами i и j не образуют полной группы событий, то есть
![]() (27)
(27)
Используя критерий минимума ошибки, искомую вероятность графически можно представить в виде суммы заштрихованных на рис. 2 площадей С и D (на этом рисунке изображены апостериорные плотности вероятностей для двух рассматриваемых гипотез). В соответствии с рисунком можно записать два равенства:
![]()
![]() (28)
(28)
Суммируя их, получим:
А + В + 2(С + D) = Pi+ Рj (29)
Нетрудно заметить, что:
![]() (30)
(30)
Следовательно, искомая вероятность ошибки равна:
![]() (31)
(31)
Для оценки интеграла (31) применим неравенство Шварца:
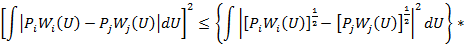
![]()
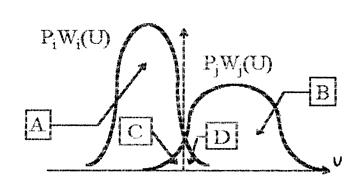
Рис. 2. К вопросу о нижней границе вероятности ошибки
После преобразования правой части (32) получим:
![]() (33)
(33)
Следовательно
![]() (j/i)
(j/i)![]() (i/j)
(i/j)![]() (34)
(34)
где
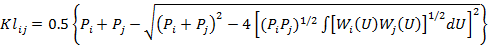 (35)
(35)
Это выражение можно представить в виде:
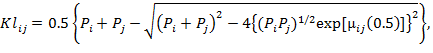 (36)
(36)
где ![]() (37)
(37)
Выражение (35) представляет собой обобщение границ Кайлата для двух гипотез i и j, не образующих полной группы событий.
Окончательно (26) запишем в виде
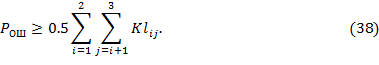
По аналогии с (26) и (27) можно найти нижнюю границу вероятности ошибки для любого числа конкурирующих гипотез. В общем случае проверки М+1 гипотез имеем:
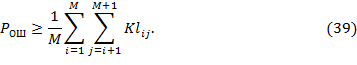
Приведенные выше выкладки получены для случая, когда наблюдаемые данные представляют собой скалярную величину. Однако все результаты справедливы, если наблюдаемые данные имеют векторный характер. Изменения при этом затрагивают только выражение (37) для логарифма производящей функции моментов, которое принимает следующий вид:
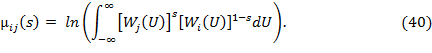
Заключение
В работе получен оптимальный (в рамках заданных условий) алгоритм обработки наблюдаемых данных с целью принятия решения о наличии сигнала, параметрах этого сигнала, а также классе принимаемого сигнала.
Конкретизация полученного алгоритма для конкретной практической задачи позволяет получить структурную схему устройства обработки, реализующего практический алгоритм решения задачи обнаружения.
Кроме того, в работе приведена методика определения вероятностных характеристик точности классификации.
Рецензенты:
Поршнев С.В., д.т.н., профессор, зав. кафедрой радиоэлектронных информационных систем, ФГАОУ ВПО «Уральский федеральный университет имени первого Президента России Б.Н. Ельцина», г. Екатеринбург.
Иванов В.Э., д.т.н., профессор, зав. кафедрой технологий средств связи, ФГАОУ ВПО «Уральский федеральный университет имени первого Президента России Б.Н. Ельцина», г. Екатеринбург.
Библиографическая ссылка
Доросинский Л.Г., Доросинский Л.Г. СИНТЕЗ И АНАЛИЗ АЛГОРИТМОВ КЛАССИФИКАЦИИ РАДИОЛОКАЦИОННЫХ СИГНАЛОВ // Современные проблемы науки и образования. 2014. № 4. ;URL: https://science-education.ru/ru/article/view?id=14116 (дата обращения: 06.03.2026).



