Задача идентификации математической модели объекта прогнозирования (ОП) основывается в выборе типа модели и оценивания её неизвестных параметров на основе анализа априорной и апостериорной (экспериментальной) информации об объекте прогнозирования.
Необходимо отметить, что в зависимости от уровня использования априорной информации об объекте различают задачи идентификации в узком и широком смысле. Идентификация в узком смысле состоит в оценивании неизвестных параметров заданного математического оператора по экспериментальной информации. При этом структура оператора (структура модели) постулируется на основе априорной информации.
Априорная информация извлекается из основных физических законов, которые заложены в основу развития постепенных отказов объекта, а также опыта эксплуатации подобных объектов. Экспериментальная информация получается в результате обработки наблюдений за параметрами объекта в процессе эксплуатации.
Цель исследования
Необходимо разработать научно-методический аппарат идентификации математической модели объекта прогнозирования в условиях неопределенности, с целью замещения объекта соответствующей моделью и последующим её исследованием.
Материал и методы исследования
К настоящему времени накоплен определенный опыт решения задач идентификации в узком смысле. Основные подходы и методы наиболее полно представлены в работах [1,2].
Однако по априорной информации удаётся обычно выявить только свойства сосредоточенности или распределённости параметров, непрерывность или дискретность протекающих процессов. Отсутствие достоверных данных о таких свойствах, как линейность или нелинейность, статичность или динамичность, стационарность или нестационарность, обусловливаемых конкретными условиями эксплуатации объекта, не позволяет априорно однозначно постулировать структуру математической модели [3].
Во многих случаях по априорной информации не удаётся выбрать даже необходимое количество существенных входных переменных, на основе которых можно достичь заданной цели. Таким образом, если при идентификации в узком смысле наблюдения используются только для оценивания неизвестных параметров модели заданной структуры, то идентификация в широком смысле позволяет по априорной и экспериментальной информации выбрать структуру модели, оценить её неизвестные параметры и проверить адекватность построенной модели реальной системе.
Результаты исследования и их обсуждение
Пусть ωi, i =
означает определённое свойство объекта, а 
– противоположное ему свойство. Тогда элемент Ωj множества
(1)
определяет логически обоснованную комбинацию наиболее общих свойств объекта, которую будем называть классом объекта.
Если в качестве ωi и соответственно понимать такие общие свойства, как сосредоточенность или распределённость параметров, линейность или нелинейность, статичность или динамичность, стационарность или нестационарность, непрерывность или дискретность, то примерами классов будут комбинации типа «объекты с сосредоточенными параметрами – нелинейные – динамические – стационарные – дискретные» или «объекты с сосредоточенными параметрами – нелинейные – динамические – стационарные – непрерывные» и т.д.
Множество Ω имеет q = 2N элементов, соответствующих различным классам ОП.
Принципиальной особенностью процесса формирования новых знаний об объекте прогнозирования является его замещение соответствующей моделью с последующим её исследованием.
Пусть vk, k = 
обозначает определённое наиболее общее свойство модели ОП, а 
– соответственно, противоположное ему свойство. Тогда логически обоснованная комбинация таких свойств (при условии их достаточной общности) может быть названа классом модели ОП Vl. Класс модели Vl является элементом множества
, (2)
называемого множеством классов моделей ОП.
Задача оценивания класса объекта прогнозирования сводится к построению некоторого решающего правила
, (3)
позволяющего на основе анализа априорной AI и апостериорной Y (экспериментальной) информации некоторым наилучшим способом сопоставить конкретному классу объекта соответствующий класс модели. Вследствие ряда обстоятельств, к которым относятся принципиально случайный характер изменения входных и выходных параметров объекта, искажённость результатов измерений параметров случайными помехами, возможная неполнота множества классов моделей (когда не все свойства объекта покрываются соответствующими свойствами модели), как правило, отсутствует принципиальная возможность построения решающего правила Фкл с нулевой вероятностью ошибочных решений [4].
Следовательно, решение задачи (3) приводит, в общем случае, к некоторой оценке класса объекта прогнозирования, называемой классом модели ОП.
Установление класса модели на основе анализа информации об объекте составляет первый (высший) уровень идентификации типа прогнозирующей модели.
Второй уровень связан с выбором структуры модели внутри некоторого выбранного класса Vl. Под структурой модели понимается вид математического оператора, известного с точностью до его параметров. Параметры могут быть как непрерывными, так и дискретными величинами (например, порядки авторегрессии и скользящего среднего в моделях Бокса – Дженкинса [5] являются дискретными параметрами, а соответствующие коэффициенты – непрерывными).
Третий уровень связан непосредственно с оцениванием значений параметров модели ОП по экспериментальным данным. Необходимо отметить различие между понятиями класса и структуры модели. Как следует из вышеизложенного, понятие класса отражает только основные свойства объекта или модели. В одном и том же классе моделей могут быть использованы различные математические операторы. Например, в классе моделей «модели с сосредоточенными параметрами – нестационарные в узком смысле – аналитические – дискретные – индивидуальные – на основе большой выборки наблюдений» могут использоваться операторы авторегрессии скользящего среднего Бокса – Дженкинса [5], экспоненциального сглаживания Брауна [6] и другие. А в классе «модели с сосредоточенными параметрами – нестационарные в узком смысле – динамические – дискретные – комбинированные (ансамблево-индивидуальные – на основе малой выборки наблюдений» имеется единственный математический оператор Силина – Заковряшина [7].
Следовательно, при такой постановке вопроса число возможных операторов в общем случае больше числа классов систем и моделей. Установлением класса модели сужается первоначальная совокупность возможных операторов, а в некоторых классах имеется только один-два эквивалентных математических оператора.
В принципе, задачу можно ставить и таким образом, чтобы в качестве элемента Vl понимать один оператор. Но тогда сильно возрастает число элементов множества V и появляются существенные трудности при выделении из наблюдений характерных признаков каждой структуры модели. В этом направлении более легко реализуемым является многоуровневый подход – на первом уровне определяется принадлежность объекта к одному из основных классов, внутри которого далее вводятся новые подклассы и т.д.
Принцип многоуровневой идентификации показан на рис. 1.
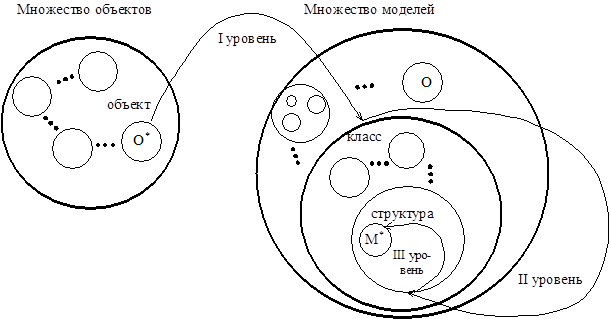
Рис. 1. Принцип многоуровневой идентификации модели объекта прогнозирования
В формализованном виде процедура многоуровневой (трёхуровневой) идентификации прогнозирующей модели может быть записана в виде системы отношений:
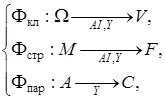(4)
где Фкл, Фстр, Фпар – есть решающие правила, которые на основе анализа априорной AI и экспериментальной Y информации (наблюдений) позволяют последовательно оценить класс модели из множества V, структуру модели из множества F и по экспериментальной информации определить значения параметров модели на множестве их значений С.
Задача оценивания класса модели ОП (задача (3)) в ряде случаев может быть решена методами дискриминантного анализа.
При этом используются так называемые дискриминантные функции di(z) от вектора признаков z, который формируется на основе совместного анализа априорной и экспериментальной информации об объекте прогнозирования. Дискриминатные функции выбираются таким образом, чтобы для всех значений z, соответствующих классу Vi, выполнялись неравенства:
di(z) > dj(z), если i ¹ j. (5)
Класс модели можно определить по номеру дискриминантной функции, имеющей наибольшее значение для наблюдаемого вектора признаков z. Тогда нерандомизированное решающее правило представляется в виде
, (6)
где s = 2n.
Вектор признаков z может быть составлен как непосредственно из наблюдений за входом и выходом исследуемого объекта, так и получаться путём известного преобразования z = L(y, u) от векторов y, u, координаты которых – измеряемые значения выходных и входных параметров объекта. Случайный характер наблюдений (а тем самым и признаков) приводит к дискриминантным функциям вида
, (7)
где рj – априорная вероятность класса Vj; Пij – потери, обусловленные отнесением i=го класса к j-му; p(z|Vj) – плотность условного распределения вероятностей признаков z для класса Vj. Отметим, что технические возможности и имеющиеся ресурсы могут быть учтены при выборе вероятностей pj, искусственно отдавая априорное предпочтение некоторых из классов Vj.
Заключение
Как уже отмечалось, по ряду причин нельзя построить метод идентификации с нулевой вероятностью ошибочных решений. Кроме того, вследствие влияния объективных факторов могут изменяться условия, в которых осуществляется моделирование. Это в равной степени относится как к характеристикам самого объекта, так и объёму и качеству исходных данных об изменении его параметров. В этих условиях процесс идентификации в виде цепочки «наблюдение – выбор структуры модели – оценивание параметров – проверка адекватности» в общем случае является многошаговым. Иными словами, если степень адекватности построенной модели недостаточна для достижения поставленной цели, задачу идентификации необходимо решать сначала, используя приобретённый опыт и стараясь получить дополнительную информацию из наблюдений.
Рецензенты:
Смагин В.А., д.т.н., профессор, профессор кафедры ФГКВОУ ВПО «Военно-космическая академия имени А.Ф. Можайского» Министерства обороны РФ, г. Санкт-Петербург.
Миронов А.Н., д.т.н., профессор, профессор кафедры ФГКВОУ ВПО «Военно-космическая академия имени А.Ф. Можайского» Министерства обороны РФ, г. Санкт-Петербург.
Библиографическая ссылка
Миронов Е.А., Платонов С.А. РЕШЕНИЕ ЗАДАЧИ ИДЕНТИФИКАЦИИ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ОБЪЕКТА ПРОГНОЗИРОВАНИЯ В УСЛОВИЯХ НЕОПРЕДЕЛЕННОСТИ // Современные проблемы науки и образования. – 2014. – № 4. ;URL: https://science-education.ru/ru/article/view?id=14029 (дата обращения: 21.11.2024).