Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Симоненков В.С. 1 Симоненкова В.А. 2

---

1 ГОУ ВПО «Оренбургский государственный университет»

2 ГОУ ВПО «Оренбургский государственный аграрный университет»

Проведен анализ влияния на радиальный прирост сосны обыкновенной климатического и биотического факторов в очагах массового размножения сосновых пилильщиков на территории Оренбургской области. Многолетние циклические колебания режимов солнечной активности, температуры и осадков вызывают синхронные колебания радиального прироста сосны обыкновенной. Радиальный прирост сосны зависит от вспышек массового размножения сосновых пилильщиков, при которых наблюдается сильная дефолиация сосны. Солнечная активность оказывает более сильное воздействие на радиальный прирост спустя два года. На радиальный прирост сосны обыкновенной доказано влияние ГТК августа текущего и следующего года, ГТК июля спустя два года, а также частичное влияние ГТК июня спустя два года. Связь между радиальным приростом деревьев и климатическими параметрами не всегда однозначна, поскольку на прирост деревьев обычно влияет комплекс факторов.

Статья в формате PDF

438 KB

сосновые пилильщики

биотический фактор

климатический фактор

сосна обыкновенная

радиальный прирост

1. Гурский А.Ак., Гурский А.Ан. Совершенствование методов оценки насаждений и ведения хозяйства в лесах Оренбургской области и Северного Казахстана. – Оренбург: ОГАУ, 2011. – 404 с.

2. Митряйкина А.М. Геоэкологическая оценка влияния гелиоклиматических факторов на радиальный прирост деревьев: автореф. дисс. канд. географ. наук. – Белгород, 2006. – 24 с.

3. Симоненкова В.А. Анализ возникновения и развития вспышек массового размножения основных листогрызущих вредителей / В.А. Симоненкова // Известия Оренбургского государственного аграрного университета. – Оренбург, 2011. – № 2. – С. 242 – 244.

4. Симоненкова В.А., Сагидуллин В.Р., Борников А.В. Влияние зоогенной дефолиации на прирост сосны обыкновенной в условиях Оренбургской области // Известия Оренбургского государственного аграрного университета. – Оренбург, 2013. – № 3. – С. 240 – 242.

5. Скомаркова М.В., Ваганов Е.А., Вирт К., Кирдянов А.В. Климатическая обусловленность радиального прироста хвойных и лиственных пород деревьев в подзоне средней тайги Центральной Сибири // География и природные ресурсы. – 2009. - № 2. – С. 80 – 85.

6. Тимофеев А.В. Динамика прироста сосны обыкновенной (Pinus sylvestris L.) под влиянием естественных и антропогенных факторов в условиях лесостепного Поволжья: дисс. …канд. геогр. наук. – СПб., 2003. – 275 c.

Важную роль в динамике прироста сосны обыкновенной (Pinus sylvestris L.) играют экотопические условия. Многолетние циклические колебания режимов солнечной активности, температуры и осадков вызывают синхронные колебания радиального прироста сосны обыкновенной [3]. Скомаркова М.В., Ваганов Е.А., Вирт К., Кирдянов А.В. [5] проводили дендроклиматические исследования годичных колец ели, пихты, сосны, березы и осины, произрастающих в подзоне средней тайги Центральной Сибири. Авторами показано, что в данных условиях влияние климатических факторов объясняет не более 53,5% изменчивости величины радиального прироста. Митряйкиной А.М. [2] были изучены максимально разнородные древесные спилы дуба черешчатого и сосны обыкновенной, индивидуальная и паратипическая изменчивость в динамике радиального прироста, особенности формирования годичных колец в условиях типичной лесостепи Среднерусской возвышенности. Между солнечной активностью (в пределах 11-летнего цикла) и величиной радиального прироста деревьев существует прямая связь со сдвигом максимума прироста от максимума солнечной активности в 1 год.

Тимофеев А.В. [6] в своей работе указывал, что режимы основных экологических факторов (солнечной активности, температуры, увлажненности) имеют циклический характер и вызывают синхронные колебания радиального прироста сосны обыкновенной.

Радиальный прирост сосны зависит от вспышек массового размножения сосновых пилильщиков, при которых наблюдается сильная дефолиация сосны (рис. 1) [4].

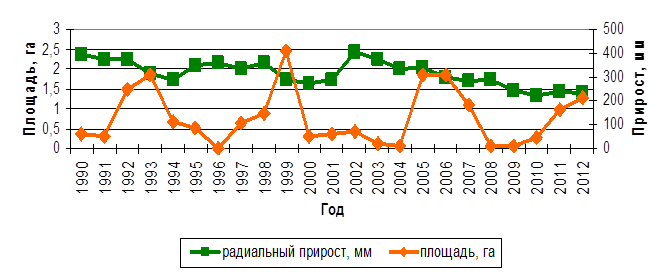
Рис. 1. Динамика радиального прироста сосны обыкновенной и очагов массового размножения сосновых пилильщиков в Соль-Илецком лесничестве

При проведении исследований зависимости радиального прироста сосны обыкновенной от ряда экологических факторов в условиях Оренбургской области оказалось трудно подобрать чистые насаждения, произрастающие без сильного воздействия хвоегрызущих филлофагов. Все насаждения сосны обыкновенной на территории Оренбургской области произрастают в очагах массового размножения сосновых пилильщиков, а также корневой или сосновой губки. Поэтому, для сравнения был использован график динамики радиального прироста сосны обыкновенной степных боров, построенный Гурским А.А. [1].

Таблица 1

Значимость воздействия на радиальный прирост сосны каждого из рассматриваемых климатических и биотических факторов

По данным Гурского А.А. [1] отмечено, что осадки, температура и влажность воздуха за апрель, сентябрь на величину радиального прироста сосны обыкновенной влияния не оказывают. По динамике индексов радиального прироста автором установлены периоды усиленного, частично умеренного роста и периоды угнетения – замедленного роста.

Для выяснения значимости воздействия на радиальный прирост сосны обыкновенной каждого из рассматриваемых климатических и биотических факторов проведен однофакторный регрессионный анализ. Исходя из предположения, что зависимость прироста от рассматриваемого фактора описывается параболой третьего порядка: Y = a1*X3 + a2*X2 + a3*X + a4, где Y – прирост сосны, мм; а1…а4 – константы уравнения; Х – значение того или иного фактора), были составлены уравнения.

Для многофакторного анализа были взяты независимые переменные, константы при которых оказались статистически значимыми (из табл. 1: ГТК_август; ГТК_август спустя год; ГТК_июль спустя два года). В результате расчетов модель оказалась статистически не значимой (р > 0.05); F (9, 8) = 1,7593; R2 = 0,664 (в программе Statistica 8.0).

Где ГТК_VIII – ГТК_август_текущего года; ГТК_VIII_1 – ГТК_август_следующего года; ГТК_VII_2 – ГТК_июля_два года спустя. Применяя пошаговую (с шагом назад) регрессию (в программе JMP) с использованием пороговых значений р, получили следующую статистически значимую модель: F (3; 16) = 3,633; р = 0,036; R2 = 0,41.

В данной программе (JMP) для удобства автоматически осуществляется отцентровка (из значений переменных возводимых в ту или иную степень вычитывается среднее значение данной переменной за период наблюдений). Курсивом выделены статистически значимые переменные. Данная модель адекватно описывает влияние ГТК_июля на прирост сосны спустя два года.

В качестве эксперимента ниже рассмотрена расширенная модель, включающая все переменные. Применяя пошаговую (с шагом вперед) регрессию (в программе JMP) с использованием пороговых значений р, получили следующий результат F (6; 3) = 9,2119; р = 0,048; R2 = 0,95.

В расширенную модель не включена «солнечная активность». Результат следующей пошаговой регрессии (с шагом вперед): F (8; 9) = 16,307; р = 0,0002; R2 = 0,94.

В следующую модель включаем все рассматриваемые независимые переменные (факторы) из предположения, что каждая независимая переменная действует на прирост сосны в текущем году.

Результат пошаговой (с шагом вперед) регрессии: F (5; 13) = 4,838; р = 0,0102; R2 = 0,65. В конечную модель включаем все переменные, за исключением солнечной активности). Результат пошаговой (с шагом вперед) регрессии: F(13; 3) = 11,7093; р = 0,033; R2 = 0,98.

На рисунках 2, 3 показано влияние солнечной активности на радиальный прирост сосны обыкновенной в условиях Оренбургской области. Солнечная активность оказывает более сильное воздействие на радиальный прирост спустя два года, что согласуется с данными Гурского А.А. [1].

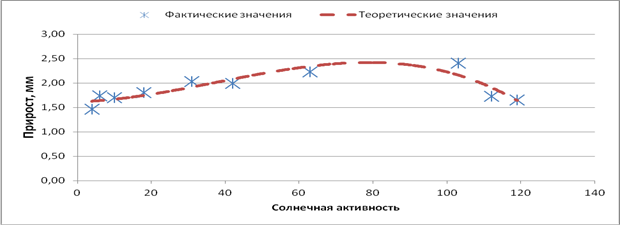
Рис. 2. Влияние солнечной активности на радиальный прирост сосны (звездочки – фактические значения, линия – теоретические значения прироста)

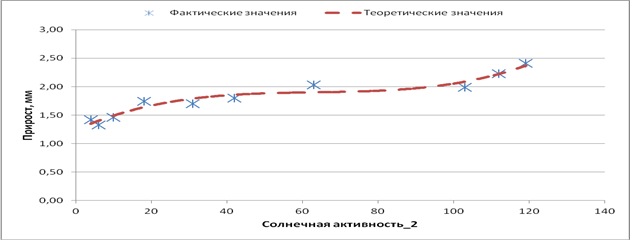
Рис. 3. Влияние солнечной активности спустя два года на радиальный прирост сосны (звездочки – фактические значения, линия – теоретические значения прироста)

На радиальный прирост сосны обыкновенной доказано влияние ГТК августа текущего и следующего года, ГТК июля спустя два года, а также частичное влияние ГТК июня спустя два года (рис. 4, 5, 6), что подтверждается данными Гурского А.А. [7], что относительная влажность воздуха и ГТК в большей мере оказывают влияние на величины индексов радиального прироста сосны обыкновенной.

На рисунках 7 – 10 показана динамика абсолютного радиального прироста сосны обыкновенной за 10, 18, 19 лет. Наиболее точно описывает динамику прироста уравнение регрессии, включающее все независимые переменные табл. 45: F (13; 3) = 11,7093; р = 0,033; R2 = 0,98.

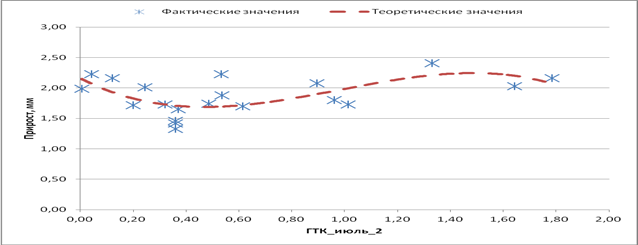
Рис. 4. Влияние ГТК июля на радиальный прирост сосны спустя два года (звездочками показаны фактические значения, линия описывает теоретические значения)

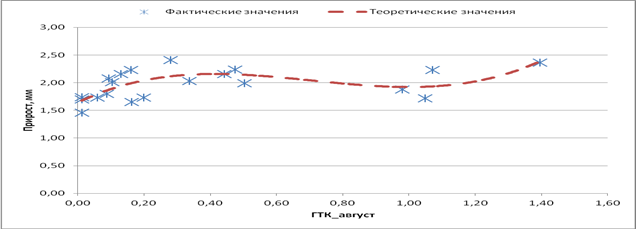
Рис. 5. Влияние ГТК_VIII на радиальный прирост сосны (звездочки – фактические значения; линия – теоретические значения)

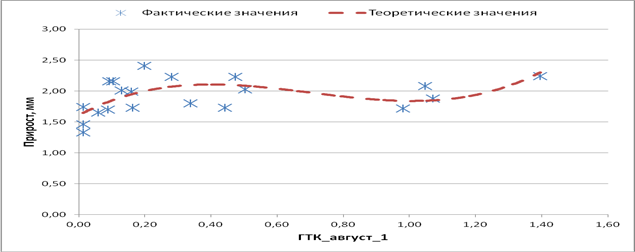
Рис. 6. Влияние ГТК_август спустя год на радиальный прирост сосны (звездочки – фактические значения; линия – теоретические значения)

В целом, на радиальный прирост сосны отмечено влияние климатических и биотических факторов, которые воздействуют с различной интенсивностью.

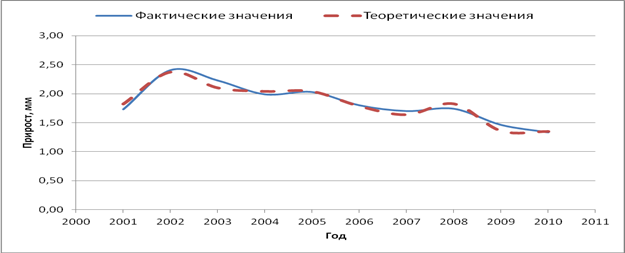
Рис. 7. Динамика прироста за 10 лет (теоретические значения получены по уравнению)

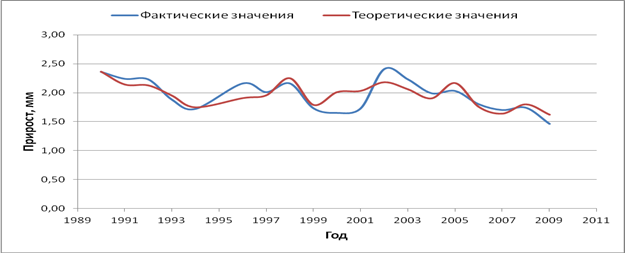
Рис. 8. Динамика прироста за 19 лет (теоретические значения получены по уравнению)

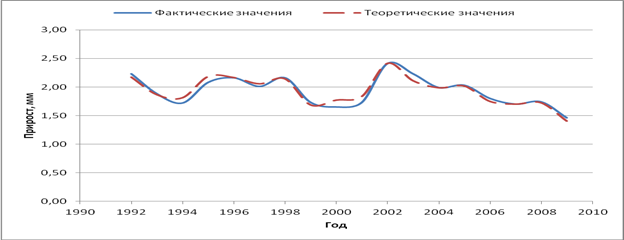
Рис. 9. Динамика прироста за 18 лет (теоретические значения получены по уравнению)

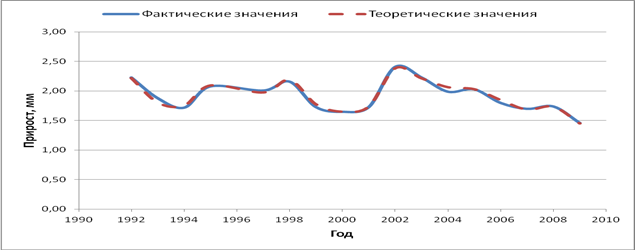
Рис. 10. Динамика прироста за 18 лет (теоретические значения получены по уравнению)

Рецензенты:

Колтунова А.И., д.с.-х.н., профессор, зам. директора института агротехнологий и лесного дела, Оренбургский государственный аграрный университет, г. Оренбург.

Абаимов В.Ф., д.с.-х.н., профессор, кафедра лесоведения, ботаники и физиологии растений, институт агротехнологий и лесного дела, Оренбургский государственный аграрный университет, г. Оренбург.

Библиографическая ссылка