Процессы сближения-стыковки-расхождения (ССР) космических аппаратов (КА) на околоземной орбите в автономном режиме уже многие годы остаются во внимании специалистов в силу целого ряда проблем. Это связано не только со сложностью собственно математического описания относительного движения пассивного и активного аппаратов (АА), сколько в принятии обоснованных допущений модели этого движения и методологии синтеза управляющих воздействий на двигательные установки (ДУ) КА [1,4,9].
Вопросам синтеза оптимального управления ДУ КА посвящено достаточно много публикаций, однако вопросам исследования возможностей формирования многомерного управления КА с использованием моделей эталонного относительного движения АА в процессах ССР двух КА уделено крайне малое внимание.
В связи с изложенным, следует считать вполне оправданным при исследовании управляемого движения КА применение методов имитационного моделирования, основанных на применении эталонных моделей (ЭМ) относительного движения КА.
Целью работы является разработка ЭМ ближнего относительного движения КА и формирование непрерывных (квазинепрерывных) управляющих ускорений центра масс АА, формируемых электрореактивными двигательными установками малой тяги (ДУ МТ), и обеспечивающих оптимальные по быстродействию и точности траектории сближения по двум ортогональным осям визирной системы координат (ВСК).
К основным традиционным допущениям при математическом описании относительного движения КА при автономном управлении процессами ССР с применением наиболее распространенной ВСК относят, как правило, следующие [1,9]:
-
Земля рассматривается как единственный центр притяжения и является однородной сферической массой;
-
орбита ПА предполагается круговой;
-
относительная малость дистанции между КА по линии визирования (ЛВ) в процессе автономного управления активным аппаратом по отношению к радиусу орбиты;
-
отсутствие сил аэродинамического сопротивления (сопротивления атмосферы) при движении обоих КА;
-
сила давления солнечного света пренебрежимо мала и др.
Перечисленные выше допущения, как отмечается в ряде исследований [1,4,8,9], являются общепринятыми в задачах синтеза оптимального управления ДУ МТ, создающими управляющие ускорения, приложенными ортогонально к центру масс АА. Эту функцию на этапе ближнего сближения выполняют координатно-реактивные двигатели, отвечающие, в общем случае, за функции сближения и ориентации КА. В качестве ДУ МТ, как отмечается в [7,10], представляется целесообразным применение электрореактивных ДУ на основе того или иного принципа работы.
Математическая модель процесса ССР с учетом перечисленных выше допущений представляется в виде [1,9]:
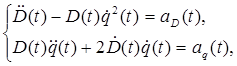(1)
где 
– соответственно фазовые относительные переменные, характеризующие линейное расстояние (дистанцию) между стыковочными узлами КА по ЛВ, относительные линейная скорость и ускорение аппаратов;
– фазовые относительные переменные, характеризующие угловые скорость и ускорение поворота ЛВ в плоскости орбиты сближающихся аппаратов;
, 
– ортогональные ускорения центра масс АА, направленные соответственно по ЛВ и перпендикулярно ей в плоскости орбиты, в первом приближении пропорциональные сигналам управления ДУ МТ.
Заметим, что процесс управляемого движения КА в форме (1) описывается системой нелинейных дифференциальных уравнений. Решение их относительно управляющих ускорений при заданных начальных и граничных условиях может быть получено лишь в частных случаях. Например, в [8] реализуют оптимальное управление угловой скоростью ЛВ при постоянстве линейной скорости сближения вдоль ЛВ. В общем случае процесс оптимального управления, как правило, сводят к расчету последовательности и длительности импульсов скорости посредством генерации в определенные моменты времени импульсов постоянной тяги ДУ по двум ортогональным смещениям центра масс АА в ВСК [1,4].
Управляющие ускорения (заданные приращения импульсов скорости) допустимо рассматривать как ступенчатые функции лишь при длительных полетах и дальнем сближении КА, что недопустимо при ближнем сближении. При этом, современные, в частности, электрореактивные ДУ МТ, способны генерировать не только импульсы постоянной тяги, но и непрерывные на некотором интервале времени законы изменения тяги [3,7]. Это означает, что ортогональные управляющие ускорения и в общем случае могут рассматриваться как непрерывные или квазинепрерывные функции времени, например при широтно-импульсном управлении ДУ.
В уравнениях (1) относительного движения КА фигурируют пять переменных состояния – три линейных и две угловых фазовых переменных. В общем случае, в любом механическом движении, в том числе и механике КА, можно выделить четыре фазовых переменных: рывок, ускорение, скорость и положение. Заметим, что старшей производной координат по времени в уравнениях (1), является координата ускорения, и рывок как фазовая переменная отсутствует. Однако, это не означает, что в ЭМ относительного движения его не должно быть.
Известно достаточно много оптимальных в том или ином понимании систем управления (СУ) и методов их синтеза [2], причем, в понятиях классической теории управления замкнутые СУ обычно отвечают динамическим свойствам оптимальных фильтров. Результатом синтеза таких СУ являются регуляторы и корректирующие звенья, содержащие параметры пропорционального, интегрального и дифференциального преобразования ошибки регулирования. Вместе с тем, как известно [2], такие СУ обеспечивают лишь компромиссное качество управления между быстродействием отработки типовых задающих воздействий и колебательностью, причем процессы отработки двигательными установками заданных управляющих ускорений длятся теоретически бесконечно долго, что создает проблемы при оценке установившихся параметров относительного движения. Кроме того, методы классической теории управления ориентированы преимущественно на синтез скалярных линейных систем управления, а рассматриваемая модель (1) описывает многомерный нелинейный процесс. В связи с этим, предлагается управляемое относительное движения КА осуществлять по принципу терминального управления (за конечное время) с применением ЭМ.
Обобщенная функционально-структурная схема имитационной модели ближнего относительного движения КА приведена на рисунке. 1.
Эталонные модели ЭМ1 и ЭМ2 представляют собой замкнутые подсистемы, функционально состоящие из последовательно соединенных дискретных устройств управления УУ1, УУ2 и подобъектов третьего порядка – тройных интеграторов. Выходы эталонных моделей – фазовые переменные относительного движения КА. Будем называть модель вычисления ортогональных ускорений центра масс АА в функции линейных и угловых фазовых переменных (положений, скоростей и ускорений) прямой задачей кинематики КА об управляющих ускорениях – ПЗКУУ. Тогда в качестве модели ПЗКУУ можно принять нелинейные дифференциальные уравнения (1).
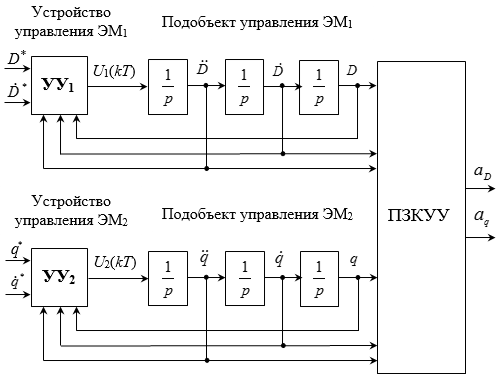
Рис 1. Обобщенная функционально-структурная схема имитационной модели формирования управляющих ускорений
В качестве задающих воздействий первой ЭМ1 рассматриваются требуемая дистанция между КА и относительная линейная скорость, второй ЭМ2 – угол и угловая скорость ЛВ. Однако, далеко не все фазовые переменные непосредственно контролируются системой контроля параметров относительного движения КА [3], в частности системой «Курс-НА». В любом случае контролируются линейные расстояния и скорость, а также угловая скорость смещения ЛВ. Кроме того, бортовые акселерометры могут измерять компоненты ортогональных ускорений в центре масс АА, а наблюдающие устройства – оценивать линейное и угловое ускорения, входящие в уравнения (1).
В зависимости от состава контролируемых переменных относительного движения и заданных переменных эталонные модели ЭМ1 и ЭМ2 могут быть редуцированы до упрощенных моделей 2-го порядка. При этом, естественно, изменится форма управляющих ускорений, формируемых ДУ МТ.
Дискретно-непрерывные математические модели ЭМ1 и ЭМ2, представленные на рис. 1, могут быть записаны в векторно-матричной форме [2,5,6]:
, (2)
где Xм(t) – вектор фазовых переменных модели, 
для ЭМ1, 
для ЭМ2,
– управляющее воздействие модели, 
для ЭМ1, 
для ЭМ2,
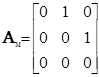– матрица состояния ЭМ (для обеих моделей),
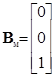– матрица управления ЭМ (для обеих моделей).
Оптимальное по критерию быстродействия дискретное управление получим, воспользовавшись методикой, приведенной в [6]. В концепции терминальных систем управления такое управление обеспечивает одновременно минимум интегральной ошибки отработки задающих воздействий при их нуль-интерполяции и линейной интерполяции. При этом, оптимальные процессы будут иметь место при произвольных начальных значениях фазовых переменных эталонного относительного движения КА.
В соответствие с методикой синтеза [6] представим такое управление в виде линейной формы координат состояния и задающих воздействий, изменяемых в дискретные моменты времени с периодом обновления, равном T, будет иметь вид:
, (3)
где 
– задающие фазовые переменные модели, 
для ЭМ1, 
для ЭМ2.
Для периода управления T = 1 с матрицы оптимального управления 
будут иметь значения: 
, 
, 
.
Схема имитационной модели формирования эталонных переменных относительного движения КА и оптимальных управляющих воздействий в среде MatLab/Simulink при произвольных начальных значениях фазовых переменных приведена на рисунке 2.
На рисунке 3 приведены кривые переходных процессов. Начальные условия фазовых переменных в системе «СИ» приняты следующими:
для ЭМ1, 
для ЭМ2.
Задающие воздействия на входах ЭМ: 
для ЭМ1, 
для ЭМ2.
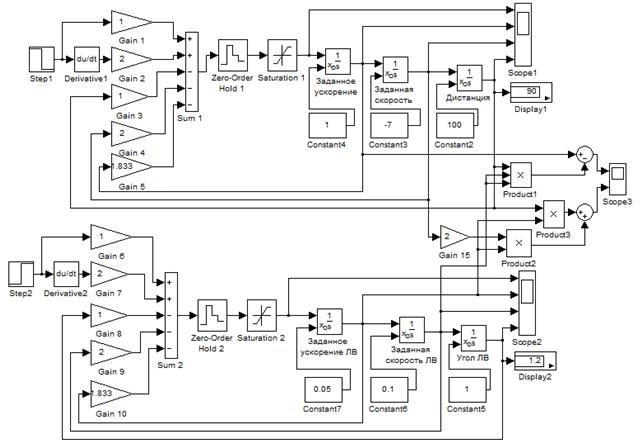
Рис. 2. Схема имитационной модели в среде MatLab/Simulink
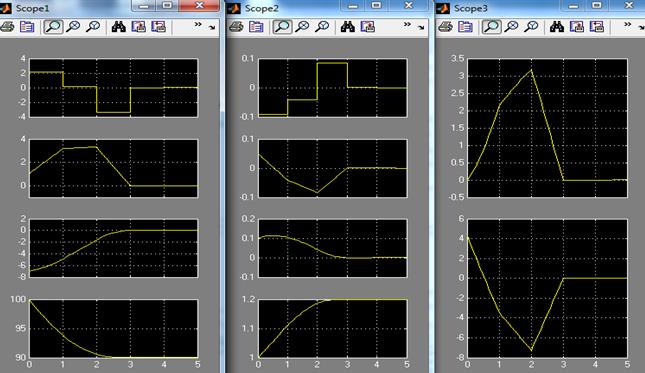
а) б) в)
Рис. 3. Переходные процессы в имитационной модели:
а) в эталонной модели ЭМ1, б) в эталонной модели ЭМ2, в) на выходе модуля ПЗКУУ
Как следует из анализа кривых, эталонное относительное движение КА оптимально по критерию быстродействия, характер изменения фазовых переменных (см. рис. 3а, 3б), а также управляющих ускорений , 
(см. рис. 3в) соответствует заданному терминальному движению КА без перерегулирования за конечное время, равное 3-м тактам дискретного управления. При этом, дискретные управляющие воздействия самих эталонных моделей реализуют оптимальное изменение самой быстрой фазовой переменной – рывка (верхние графики на рис. 3а, 3б).
Выводы
Представленный в статье подход к формированию ортогональных управляющих ускорений КА в процессах их сближения-стыковки-расхождения базируется на применении дискретно-непрерывных эталонных моделей относительного движения КА, что создает принципиальную возможность получения ряда конкурентных преимуществ:
-
реализовать оптимальные по критериям быстродействия и точности законы изменения фазовых переменных, причем при произвольных начальных значениях контролируемых фазовых переменных;
-
сформировать в реальном времени непрерывные или квазинепрерывные, в частности, широтно-импульсные, управляющие воздействия на системы управления сближающе-корректирующими ДУ МТ;
- осуществить сколь угодно мягкое касание стыковочных узлов путем программного снижения линейных и угловых скоростей при уменьшении дистанции между КА;
-
реализовать возможность оптимизации одновременного процесса сокращения дистанции между КА и поворота ЛВ в заданную позицию;
- реализовать в полной мере энергетические ресурсы ДУ МТ и самого активного корабля, варьируя тактом дискретного управления и величинами приращений задающих воздействий на уровне эталонных моделей: чем меньше такт управления и больше приращения задающих воздействий, тем большими энергетическими ресурсами должны обладать ДУ, развивая большие импульсы скорости КА на такте управления и, соответственно, наоборот.
Если задающие воздействия на входах ЭМ формируются квантователями нулевого порядка, то из структуры ЭМ целесообразно исключить составляющую, пропорциональную производной задающего воздействия.
Рецензенты:
Бочкарев С.В., д.т.н., доцент, профессор кафедры микропроцессорных средств автоматизации, Пермский национальный исследовательский политехнический университет, г.Пермь.
Цаплин А.И., д.т.н., профессор, зав. кафедрой общей физики, Пермский национальный исследовательский политехнический университет, г.Пермь.
Библиографическая ссылка
Казанцев В.П., Даденков Д.А. ЭТАЛОННЫЕ МОДЕЛИ ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ КОСМИЧЕСКИХ АППАРАТОВ В ЗАДАЧАХ ФОРМИРОВАНИЯ УПРАВЛЯЮЩИХ УСКОРЕНИЙ ДВИГАТЕЛЬНЫХ УСТАНОВОК // Современные проблемы науки и образования. – 2014. – № 4. ;URL: https://science-education.ru/ru/article/view?id=13968 (дата обращения: 18.04.2024).