В работе [4] рассмотрена задача аппроксимации распределения содержания углерода в коксующихся углях, которое изменяется в диапазоне от ![]() до некоторого максимального значения
до некоторого максимального значения ![]() Рассматриваемая задача имеет важное практическое значение, поскольку параметры той или иной партии углей, оцениваемые по функции распределения углерода по конечному набору независимых тестовых выборок, например:
Рассматриваемая задача имеет важное практическое значение, поскольку параметры той или иной партии углей, оцениваемые по функции распределения углерода по конечному набору независимых тестовых выборок, например:
- размах возможных содержаний углерода, вероятности содержания углерода в возможном диапазоне;
- вероятности содержания углерода, находящиеся в возможном диапазоне, в частности, вероятность нормативных пределов (обеспеченность);
- фактические значения, отвечающие вероятности 95-процентного попадания измеренных величин в эти пределы (нормативная обеспеченность);
используются при торгово-промышленной маркировке угля и, следовательно, от точности их оценок зависит отпускная стоимость данной партии угля.
В [4] обосновано, что адекватной моделью подобных распределений является не обычное гауссово (нормальное) распределение, но обобщенный нормальный закон с ограниченной областью рассеяния, который возникает, например, при описании случайных блужданий броуновской частицы в ограниченной области рассеяния. Плотность вероятности случайной величины с нормальным законом распределения с ограниченной областью рассеяния описывается следующим выражением [3]:
![]() (1)
(1)
где А – нормировочный коэффициент, определяемый из условия
![]() (2)
(2)
![]()
![]()
![]()
![]() - координаты центров фиктивных источников
- координаты центров фиктивных источников
![]() размер области рассеяния,
размер области рассеяния,
![]() математическое ожидание случайной величины при отсутствии области ограничения,
математическое ожидание случайной величины при отсутствии области ограничения,
![]() СКО случайной величины при отсутствии области ограничения.
СКО случайной величины при отсутствии области ограничения.
Отметим, что, формально, распределение, является трех параметрическим (оно зависит от следующих параметров: ![]() – положение центра рассеяния, s − СКО при отсутствии ограничения, l – размаха области рассеяния). Однако, на самом деле, если принять во внимание, что
– положение центра рассеяния, s − СКО при отсутствии ограничения, l – размаха области рассеяния). Однако, на самом деле, если принять во внимание, что ![]() , где
, где ![]() − координаты, левой и правой границ области рассеяния, знание значений которых оказывается весьма важным в практических приложениях. Также стоить отметить, что, хотя в выражении присутствует бесконечная система фиктивных источников, для практических вычислений достаточно некоторого конечного числа
− координаты, левой и правой границ области рассеяния, знание значений которых оказывается весьма важным в практических приложениях. Также стоить отметить, что, хотя в выражении присутствует бесконечная система фиктивных источников, для практических вычислений достаточно некоторого конечного числа ![]() . Таким образом, распределение становится 5-параметрическим:
. Таким образом, распределение становится 5-параметрическим:
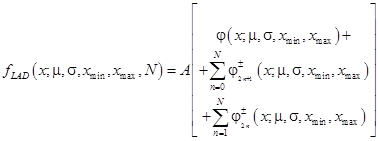 (3)
(3)
![]() (4)
(4)
Таким образом, задача состоит в следующем: априорно известно, что случайная величина описывается нормальным законом распределения с ограниченной областью рассеяния , требуется на основе экспериментальной выборки определить параметры ![]() обобщенного нормального распределения с ограниченной областью рассеяния
обобщенного нормального распределения с ограниченной областью рассеяния ![]() . Традиционно вектор параметров находят как решение задачи:
. Традиционно вектор параметров находят как решение задачи:
![]() (5)
(5)
где ![]() – тот или иной функционал, вид которого зависит от выбранного критерия близости функций.
– тот или иной функционал, вид которого зависит от выбранного критерия близости функций.
В общем случае, при любой выбранной мере приближения, нахождение ее глобального минимума в приводит к необходимости решения той или иной системы нелинейных уравнений, у которой в рассматриваемом случае не удается найти аналитические решения. Как следствие, здесь приходится использовать соответствующие численные методы (например, известен удачный опыт использования метода нелинейного программирования при выборе в качестве оптимальной меры приближения метода наименьших квадратов [4]). Однако, сходимость итерационных методов к истинному решению оказывается существенно зависящей от выбора начального приближения вектора параметров, который в большинстве случаев является, вообще говоря, самостоятельной нетривиальной задачей. (С нашей точки зрения, данное обстоятельство явилось причиной того, что на практике модель обобщенного нормального распределения с ограниченной областью рассеяния не получила такого широкого распространения, как нормальный закон распределения или усеченный нормальный закон распределения [3]).
Таким образом, оказывается актуальным расширение круга методов, используемых для нахождения значений аргументов в (5), соответствующих глобальному минимуму функции ![]() В этой связи, была изучена возможность использования в рассматриваемой задаче генетических алгоритмов, относящихся к эвристическим методам случайного поиска, которые, как ожидается [5], позволяют находить искомые решения нелинейных систем практически при любых начальных условиях.
В этой связи, была изучена возможность использования в рассматриваемой задаче генетических алгоритмов, относящихся к эвристическим методам случайного поиска, которые, как ожидается [5], позволяют находить искомые решения нелинейных систем практически при любых начальных условиях.
В статье описана методика использования генетических алгоритмов для нахождения параметров нормального распределения с ограниченной областью рассеяния.
Методика использования генетических алгоритмов в задаче оценивания параметров 5-ти параметрической функции распределения по случайной выборке
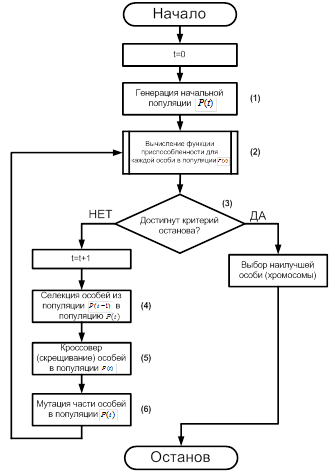
Обощенная блок-схема работы классического генетического алгоритма представлена на рисунке 1а [5].
 а)
а) 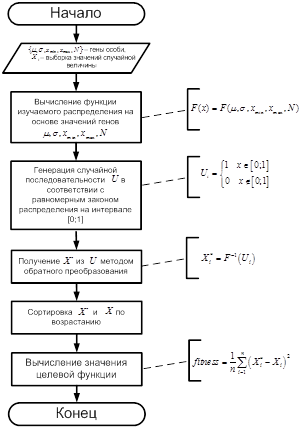 б)
б)
Рис. 1. Блок схемы классического генетического алгоритма (а) и алгоритма вычисления функции приспособленности (б): ![]() ‑ анализируемая случайная последовательность
‑ анализируемая случайная последовательность
Из рисунка 1а видно, что для применения ГА необходимо установить взаимно однозначное соответствие между основными структурными элементами: видом элемента популяции (особи), оператор кроссовера (скрещивания), мутации, селекции (отбора), видом функции приспособленности (фитнес-функции) и параметрами изучаемого распределения ![]() .
.
Напомним, что в ГА используется следующая иерархия понятий.
Популяция, которая состоит из особей. Каждая особь состоит из одной или нескольких хромосом, содержащих закодированное текущее решение рассматриваемой задачи (в данном случае, значения параметров распределения). Хромосома состоит из последовательности генов, в дискретном случае имеющих значения 0 или 1.
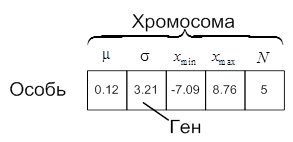
Рассматриваемая задача относится к классу оптимизационных задач в непрерывной области поиска, поэтому каждая хромосома представлялась 5-ти мерным вектором, координаты которого (гены) имели вещественные значения, соответствующие параметрам плотности распределения (3). Соответственно, отдельная особь в популяции состояла из одной хромосомы и пяти генов (рисунок 2а).
Далее решение данной задачи находилось выполнением следующей последовательности действий.
1. Формирование начальной популяции, состоящей из ![]() особей (блок 1 на рисунке 1а). (Число особей определяет производительность генетического алгоритма.) С математической точки зрения популяция есть матрица вещественных чисел
особей (блок 1 на рисунке 1а). (Число особей определяет производительность генетического алгоритма.) С математической точки зрения популяция есть матрица вещественных чисел ![]() размерности
размерности ![]() , в которой каждая строка-вектор – отдельная особь (рисунок 2б).
, в которой каждая строка-вектор – отдельная особь (рисунок 2б).
Начальная популяция в ГА, как правило, инициализируется случайным образом: каждому гену присваивается случайное число, выбираемое из генеральной совокупности с известной функцией распределения. На практике обычно используются случайные величины с равномерным распределением в ограниченной области. Следовательно, в выбранном методе определение области ограничения значений генов также является важной задачей.
2. Вычисление для каждой особи в популяции значений функции приспособленности особей (блок 2 на Рисунке 1а)
![]() (6)
(6)
где ![]() ‑
‑ ![]() -ая особь в популяции
-ая особь в популяции ![]() .
.
Блок-схема алгоритма вычисления функции приспособленности для особи ![]() представлена на рисунке 1а.
представлена на рисунке 1а.
Значения функции приспособленности используются для количественной оценки пригодности данного решения: если ![]() , то особь
, то особь ![]() более приспособлена (лучше) особи
более приспособлена (лучше) особи ![]() .
.
3. Проведение селекции (отбора) популяции (Блок 4 на рисунке 1а). Селекция – процесс, посредством которого более приспособленные особи получают большую возможность для воспроизводства потомков.
Основные виды селекции:
- Селекция на основе рулетки. При его реализации каждой особи в популяции соответствует зона на колесе рулетки, пропорционально соразмерная с величиной функции приспособленности. Тогда при повороте колеса рулетки каждая особь имеет некоторую вероятность выбора для селекции
- Элитная селекция. В этом случае выбираются лучшие (элитные) особи на основе сравнения значений функции приспособленности.
- Турнирная селекция. Согласно размеру «турнира» случайно выбирается некоторое число особей, и лучшие особи в этой группе выбираются для воспроизведения.
- Равномерная селекция. Все особи имеют равные шансы для воспроизведения
В результате выполнения селекции из популяции ![]() размером
размером ![]() особей формируется временная «родительская» популяция
особей формируется временная «родительская» популяция ![]() в количестве
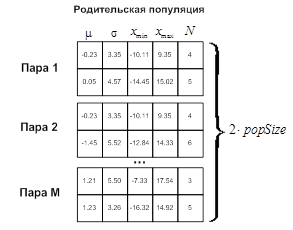
в количестве ![]() особей, сгруппированных по парам. При этом родительскую популяцию образуют выделенные более приспособленные особи (рисунок 2в).
особей, сгруппированных по парам. При этом родительскую популяцию образуют выделенные более приспособленные особи (рисунок 2в).
4. Применение к каждой паре родителей оператора кроссовера (блок 5 на Рисунке 1а). Кроссовер (скрещивание) – процесс, позволяющий на основе родительских особей получать потомков.
Основными видами кроссовера являются:
- Одноточечный кроссовер. Случайным образом выбирается точка в двух случайных хромосомах, где они должны быть «разрезаны». Меняя элементы после точки кроссовера, можно получить двух новых потомков (рисунок 2г).
- Двухточечный кроссовер. В каждой хромосоме выбираются случайным образом две точки кроссовера и хромосомы обмениваются генами.
- Многоточечный кроссовер. Выполняется аналогично.
 а)
а) 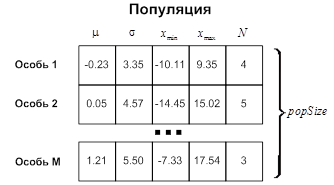 б)
б)
 в)
в) 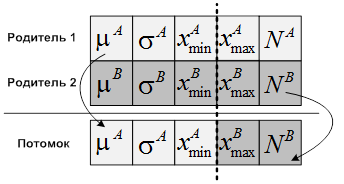 г)
г)
Рис. 2. К установлению соответствия между параметрами распределения и параметрами ГА: а – представление особи, б – пример популяции, в – родительская популяция, полученная в результате селекции, г – пример одноточечного кроссовера
Каждая родительская пара родителя производит одного потомка (Рисунок 2г). В результате из родительской популяции ![]() размером
размером ![]() особей получают популяцию следующего поколения размером
особей получают популяцию следующего поколения размером ![]() .
.
5. Выполнение мутации (этап 6 на рисунок 1а). Мутация – процесс внесения случайных изменений в хромосомы, приводящий к генетическому разнообразию популяции и позволяющий генетическому алгоритму «выбираться» из локальных экстремумов и исследовать более обширное пространство параметров.
Здесь задается число особей ![]() , которое будет подвержено мутации. На каждой итерации генетического алгоритма после кроссовера случайным образом выбирается
, которое будет подвержено мутации. На каждой итерации генетического алгоритма после кроссовера случайным образом выбирается ![]() особей из популяции
особей из популяции ![]() . Далее, для каждого гена выбранных особей задаются новые значения, выбираемые из генеральной совокупности случайных величин с заданным законом распределения.
. Далее, для каждого гена выбранных особей задаются новые значения, выбираемые из генеральной совокупности случайных величин с заданным законом распределения.
6. Проверка выполнения критерия останова. За критерий останова можно принять появление в популяции особи с функцией приспособленности меньше заданного значения ![]() или выполнения условия
или выполнения условия
![]() (7)
(7)
где ![]() ‑ среднее значение функции приспособленности в популяции,
‑ среднее значение функции приспособленности в популяции, ![]() ‑ заданная граница колебания функции приспособленности.
‑ заданная граница колебания функции приспособленности.
Если критерий останова достигнут, завершение работы алгоритма, иначе повторение действий, описанных в пп. 2–5.
Из приведенного выше описания методики использования ГА для оценки параметров распределения (3) по случайной выборке видно, что для решения поставленной задачи требуется обоснование выбора следующих параметров ГА:
- границ области изменения параметров-генов;
- размера популяции.
- способа формирования начальной популяции;
- функции приспособленности особи;
- количества особей, подвергаемых процедуре мутации;
- оператора мутации;
- оператор селекции;
- оператора кроссовера.
Обоснование выбора области поиска параметров нормального распределения с ограниченной областью рассеяния
Рекомендации по выбору областей поиска параметров основаны на результатах моделирования броуновских блужданий в ограниченной области с абсолютно упруго отражающими стенками [2], согласующимися с результатами аналитического анализа рассматриваемого движения [1], состоят в следующем:
1. В качестве значений границ области рассеяния случайной величины ![]() целесообразно использовать значения:
целесообразно использовать значения:
![]()
![]()
2. Нулевое приближении параметра ![]() нужно выбирать из отрезка
нужно выбирать из отрезка ![]() , где
, где ![]() - минимальное и максимальное значения случайной последовательности
- минимальное и максимальное значения случайной последовательности ![]()
3. Область поиска истинного значения параметра ![]() следует ограничить отрезком
следует ограничить отрезком ![]() .
.
4. Оценка нулевого приближения параметра ![]() следует получать на основе анализа зависимости
следует получать на основе анализа зависимости
![]() (8)
(8)
где ![]() усредненое по ансамблю реализаций среднеквадратическое отклонение броуновской частицы, n - число шагов броуновской частицы, получаемой с помощью статистического моделирования броуновского движения в соответствие с методикой, описанной в [2]. (Типичная зависимость
усредненое по ансамблю реализаций среднеквадратическое отклонение броуновской частицы, n - число шагов броуновской частицы, получаемой с помощью статистического моделирования броуновского движения в соответствие с методикой, описанной в [2]. (Типичная зависимость ![]() от числа шагов броуновских блужданий представлена на рисунке 3.)
от числа шагов броуновских блужданий представлена на рисунке 3.)
5. Область поиска истинного значения параметра ![]() следует ограничить отрезком
следует ограничить отрезком ![]() , где
, где ![]()
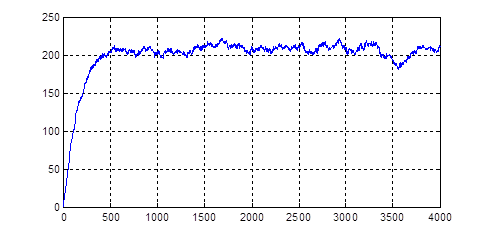
Рис. 3. Пример зависимость ![]() броуновского блуждания в ограниченной области рассеяния:
броуновского блуждания в ограниченной области рассеяния: ![]()
![]()
![]()
![]()
![]()
Необходимо отметить, что плотность распределения нормальной случайной величины (3), вообще говоря, формируется бесконечной системой фиктивных источников. Однако, расчеты показывают, что достаточная точность вычисления плотности вероятности в соответствие с (3) достигается при ![]() пар мнимых источников (соответственно, число мнимых источников -
пар мнимых источников (соответственно, число мнимых источников - ![]() ), а потому, указанную величину можно не оценивать с помощью ГА. Для иллюстрации данного утверждения на рисунке 4 представлена зависимость
), а потому, указанную величину можно не оценивать с помощью ГА. Для иллюстрации данного утверждения на рисунке 4 представлена зависимость
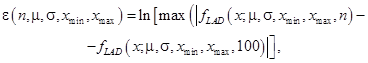
вычисленная для следующих значений параметров: ![]()
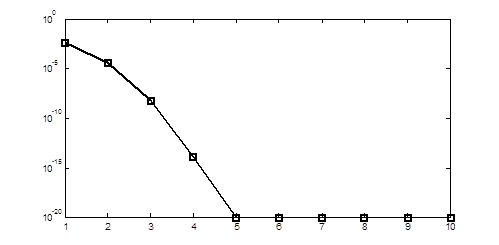
Рис. 4. График зависимости ![]()
Таким образом, методика нахождения параметров нормального распределения случайной последовательности с ограниченной областью рассеяния по случайной выборке ![]() реализуется выполнением следующей последовательности действий:
реализуется выполнением следующей последовательности действий:
- Вычисление оценки левой границы области рассеяния распределения (9)
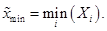
- Вычисление оценки правой границы области рассеяния распределения (9)
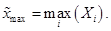
- Задание количества пар фиктивных источников
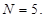
- Задание интервала ограничения для параметра
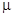 :
: 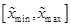 .
. - Задать интервал ограничения для параметра
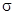 :
: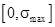 , где
, где 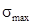 вычисляется по зависимости .
вычисляется по зависимости . - Вычислить, используя ГА, значения параметров
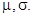
Анализ перечня действий, реализующих методику решения рассматриваемой задачи с помощью ГА, показывает, что использованные подходы к оценке ряда значений параметров распределения (3) позволяют, фактически, уменьшить размерность пространства параметров до двух - ![]()
Методика исследования влияния настроек ГА на точность оценивания параметров нормального распределения с ограниченной областью рассеяния
В ходе проведенных исследований рассмотрены были изучены нормальные распределения с ограниченной областью рассеяния со следующими параметрами: ![]()
![]()
![]()
![]() где L - размер области рассеяния, для
где L - размер области рассеяния, для ![]() различных значений интервала рассеяния -
различных значений интервала рассеяния - ![]() и
и ![]() различных положений центра распределения (3) относительно границ интервала:
различных положений центра распределения (3) относительно границ интервала: ![]() Таким образом, было изучено
Таким образом, было изучено ![]() различных распределений нормальных случайных последовательностей с ограниченной областью рассеяния.
различных распределений нормальных случайных последовательностей с ограниченной областью рассеяния.
В исследовании использовались следующие настройки ГА:
- Селекция:
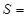 <равномерная; турнирная; на основе рулетки>;
<равномерная; турнирная; на основе рулетки>; - Мутация:
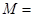 <адаптивная> (т.к. в задаче присутствуют ограничения)
<адаптивная> (т.к. в задаче присутствуют ограничения) - Кроссовер:
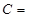 <одноточечный; двухточечный; усредненный; разбросанный, эвристический>;
<одноточечный; двухточечный; усредненный; разбросанный, эвристический>; - Доля кроссовера:
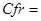 <0,3;0,6;0,9>;
<0,3;0,6;0,9>; - Доля мутации
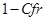 ;
; - Размер популяции:
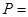 <5, 10, 25>.
<5, 10, 25>.
Таким образом, каждый эксперимент характеризовался следующим кортежем:
![]() ,
,
поэтому всего было рассмотрено
![]()
различных комбинаций настроек.
Для каждого набора настроек было выполнено ![]() независимых статистических испытаний, в ходе которых генерировались случайные последовательности
независимых статистических испытаний, в ходе которых генерировались случайные последовательности ![]()
![]() в соответствие с заданным законом распределения и, далее, следуя описанной выше методики, оценивались параметры данного распределения. Кроме того по каждому k-ому независимому испытанию оценивалась величина, характеризующее отличие между теоретической и экспериментальной функциями распределения:
в соответствие с заданным законом распределения и, далее, следуя описанной выше методики, оценивались параметры данного распределения. Кроме того по каждому k-ому независимому испытанию оценивалась величина, характеризующее отличие между теоретической и экспериментальной функциями распределения:
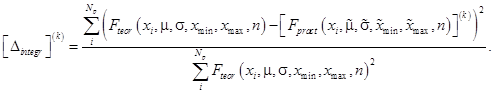
Таким образом, общее число запусков ГА составило
![]()
Анализ результатов вычислительных экспериментов
Наилучшие результаты работы ГА для каждого набора параметров распределения выбранных из результатов k независимых испытаний представлены в табл. 1, 2.
Таблица 1
Результаты оценки параметров нормального распределения с ограниченной областью рассеяния
|
№ набора параметров |
Параметры |
|
|
|
|
|
|
1 |
Теоретические значения |
0.000 |
10.000 |
-10.000 |
10.000 |
- |
|
Наилучший результат |
–1.473 |
7.968 |
–9.730 |
9.990 |
2.692∙10-2 |
|
|
2 |
Теоретические значения |
5.000 |
10.000 |
-10.000 |
10.000 |
- |
|
Наилучший результат |
3.486 |
7.788 |
-9.910 |
9.870 |
3.920∙10-3 |
|
|
3 |
Теоретические значения |
10.000 |
10.000 |
-10.000 |
10.000 |
- |
|
Наилучший результат |
5.166 |
8.547 |
–9.790 |
9.990 |
4.000∙10-5 |
|
|
4 |
Теоретические значения |
0.000 |
10.000 |
–15.000 |
15.000 |
- |
|
Наилучший результат |
–0.371 |
9.481 |
–14.925 |
14.685 |
1.590∙10-3 |
|
|
5 |
Теоретические значения |
7.500 |
10.000 |
–15.000 |
15.000 |
- |
|
Наилучший результат |
7.144 |
8.693 |
–9.915 |
14.955 |
4.600∙10-4 |
|
|
6 |
Теоретические значения |
15.000 |
10.000 |
–15.000 |
15.000 |
- |
|
Наилучший результат |
11.281 |
9.258 |
–14.775 |
14.985 |
1.000∙10-5 |
|
|
7 |
Теоретические значения |
0.000 |
10.000 |
–25.000 |
25.000 |
- |
|
Наилучший результат |
0.553 |
10.253 |
–20.775 |
24.775 |
3.320∙10-3 |
|
|
8 |
Теоретические значения |
12.500 |
10.000 |
–25.000 |
25.000 |
- |
|
Наилучший результат |
12.370 |
9.945 |
–14.025 |
24.675 |
9.000∙10-5 |
|
|
9 |
Теоретические значения |
25.000 |
10.000 |
-25.000 |
25.000 |
- |
|
Наилучший результат |
20.186 |
8.562 |
–2.625 |
24.875 |
9.000∙10-5 |
|
|
10 |
Теоретические значения |
0.000 |
10.000 |
–50.000 |
50.000 |
- |
|
Наилучший результат |
0.072 |
9.658 |
–25.650 |
25.450 |
6.000×10-4 |
|
|
11 |
Теоретические значения |
25.000 |
10.000 |
–50.000 |
50.000 |
- |
|
Наилучший результат |
24.647 |
10.339 |
–0.650 |
45.350 |
4.590∙10-3 |
|
|
12 |
Теоретические значения |
50.000 |
10.000 |
–50.000 |
50.000 |
- |
|
Наилучший результат |
47.359 |
9.736 |
13.850 |
49.950 |
1.000∙10-4 |
Таблица 2
Настройки генетического алгоритма для каждого набора параметров распределения
|
№ |
Селекция |
Мутация |
Кроссовер |
Доля кроссовера |
Размер популяции |
|
1 |
равномерная |
адаптивная |
одноточечный |
0.9 |
25 |
|
2 |
рулетка |
адаптивная |
двухточечный |
0.6 |
25 |
|
3 |
равномерная |
адаптивная |
одноточечный |
0.3 |
25 |
|
4 |
равномерная |
адаптивная |
усредненный |
0.6 |
25 |
|
5 |
турнирная |
адаптивная |
разбросанный |
0.6 |
25 |
|
6 |
турнирная |
адаптивная |
эвристический |
0.9 |
25 |
|
7 |
равномерная |
адаптивная |
эвристический |
0.3 |
25 |
|
8 |
турнирная |
адаптивная |
эвристический |
0.3 |
25 |
|
9 |
равномерная |
адаптивная |
одноточечный |
0.3 |
25 |
|
10 |
равномерная |
адаптивная |
одноточечный |
0.3 |
25 |
|
11 |
равномерная |
адаптивная |
эвристический |
0.6 |
25 |
|
12 |
турнирная |
адаптивная |
эвристический |
0.6 |
25 |
Гистограммы случайных последовательностей, теоретические функции плотности распределения и наилучшие аппроксимированные функции плотности распределения, соответствующие наборам параметров, представленным в табл. 1, представлены на рисунке 5.
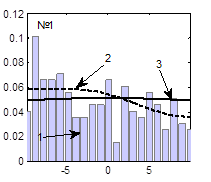
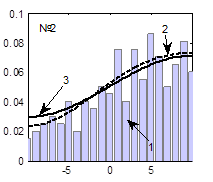
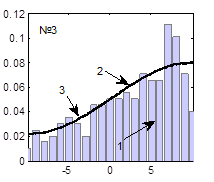
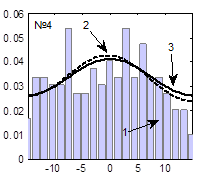
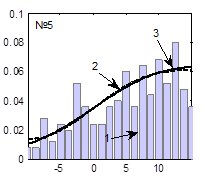
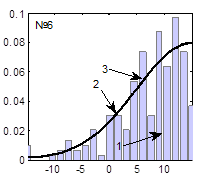
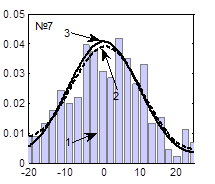
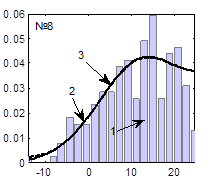
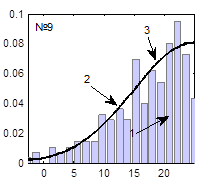
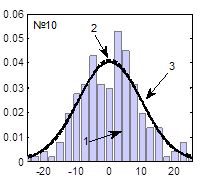
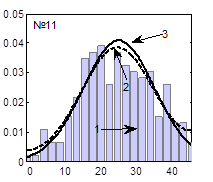
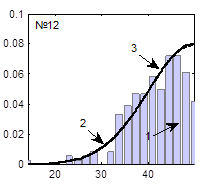
Рис. 5. Функции плотности распределения (3), при вычислении которых использованы значения параметров, представленные в табл. 1 и настройки ГА, представленные в табл. 2:
1 – гистограмма случайной последовательности, 2 – экспериментальная функция плотности распределения, 3 – теоретическая функция плотности распределения
Из таблиц 1, 2 и рисунка 5 видно, что наилучшие результаты получаются при следующих настройках ГА:
- селекция: равномерная или турнирная;
- мутация: адаптивная;
- кроссовер – одноточечный или эвристический;
- доля кроссовера находится в интервале от 0.2 до 0.7;
- размер популяции: 25-50.
Отметим, что увеличение размера популяции, увеличивает разнообразие входящих в нее особей, что, в свою очередь, увеличивает вероятность нахождения оптимального решения. Однако увеличение размера популяции пропорционально увеличивает объем, и, соответственно, время вычислений. В этой связи размер популяции приходится для каждой конкретной задачи выбирать эмпирически, исходя из соотношения между временем расчетов и точностью оценки параметров плотности нормального распределения с ограниченной областью рассеяния случайных последовательностей.
Выводы
Анализ результатов применения ГА в задаче нахождения параметров случайных последовательностей с нормальным распределением с ограниченной областью рассеяния позволяет сделать следующие выводы:
- Предложена методика нахождения параметров данного распределения, основанная на использовании ГА, и получено подтверждение ее работоспособности.
- Обоснованы рекомендации выбора областей поиска значений параметров нормального распределения с ограниченной областью рассеяния.
- Получены оценки точности оценки параметров нормального распределения с ограниченной областью рассеяния и интегрального показателя, характеризующего качество оценки изучаемой плотности распределения в целом.
- Обоснован выбор настроек ГА, обеспечивающих наилучшую точность оценок параметров нормального распределения с ограниченной областью рассеяния.
Работа выполнена в рамках договора № 02.G25.31.0055 (проект 2012-218-03-167).
Рецензенты:
Кубланов В.С., д.т.н., доцент, профессор кафедры радиоэлектроники информационных систем ГАОУ ВПО «Уральский федеральный университет им. первого Президента России Б.Н. Ельцина», г. Екатеринбург.
Доросинский Л.Г., д.т.н., профессор, заведующий кафедрой информационных технологий ГАОУ ВПО «Уральский федеральный университет им. первого Президента России Б.Н. Ельцина», г. Екатеринбург.
Криштоп В.В., д.ф.-м.н., профессор, заведующий кафедрой «Физика», Дальневосточный государственный университет путей сообщения, г. Хабаровск, профессор Университета Kwangwoon University, Korea.
Библиографическая ссылка
Поршнев С.В., Копосов А.С. МЕТОДИКА ИСПОЛЬЗОВАНИЯ ГЕНЕТИЧЕСКИХ АЛГОРИТМОВ В ЗАДАЧЕ ОЦЕНКИ ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЙ С ОГРАНИЧЕННОЙ ОБЛАСТЬЮ РАССЕЯНИЯ // Современные проблемы науки и образования. 2014. № 4. ;URL: https://science-education.ru/ru/article/view?id=13943 (дата обращения: 06.03.2026).



