Вебер-амперная характеристика (ВАХ) электротехнического устройства (ЭУ) содержит важную диагностическую информацию, позволяющую судить о работоспособности ЭУ. Нами предложен метод, базирующийся на измерении формы тока и амплитуды питающего ЭУ напряжения. В данном методе определение ВАХ основано на решении обратной задачи метода гармонического баланса (МГБ) [1].
Цель работы: разработка метода измерения ВАХ электротехнических устройств, позволяющего упростить процедуру измерения, при сохранении приемлемой точности.
Материал и методы исследований: методы гармонического баланса, теории измерений, математического моделирования в пакетах Microcap 9, Maple 15.
Результаты и обсуждение
Для получения ВАХ конкретного образца ЭУ необходимо воздействовать на магнитопровод внешним изменяющимся магнитным полем и измерять возникающий в его сечении магнитный поток. В большинстве случаев разборка ЭУ недопустима, поэтому разработан ряд методов получения ВАХ [2], где в качестве источника внешнего магнитного поля используется катушка ЭУ, а поток получают косвенным образом из уравнения цепи.
Недостаток этих методов в том, что в их основе лежит операция интегрирования, кроме того, активное сопротивление катушки изменяется из-за нагрева. Необходимость нивелирования этих факторов инициировало ряд работ, в той или иной степени удачно решающих проблему [4; 7]. Погрешность этих методов 5 – 6%.
На наш взгляд, для получения ВАХ ЭУ необходимо использовать решение обратной задачи метода гармонического баланса (МГБ) [5; 6].
Решение прямой задачи МГБ позволяет определить форму тока i(t), протекающего через элемент цепи с нелинейной индуктивностью (НИ), заданную в виде ряда Фурье:
![]() , (1)
, (1)
где I (2m+1) – амплитуда (2m+1)-й гармоники тока, w – угловая частота. При этом должна быть известна форма напряжения, приложенного к НИ:
![]() , (2)
, (2)
где Ua – амплитуда приложенного к нелинейной индуктивности напряжения;
а также ее ВАХ, заданная аппроксимирующим выражением:
![]() , (3)
, (3)
где ψ – значение магнитного потокосцепления через НИ, k (2m+1) – коэффициенты аппроксимирующего ВАХ выражения, ![]() , (n+1) – количество слагаемых в аппроксимирующем выражении, i – сила тока через НИ.
, (n+1) – количество слагаемых в аппроксимирующем выражении, i – сила тока через НИ.
Обратная задача МГБ формируется следующим образом.
Имеется НИ с неизвестной ВАХ, известны законы изменения, приложенного к НИ напряжения (2) и протекающего по ней тока (1). Требуется определить коэффициенты k(2m+1) аппроксимирующего ВАХ выражения (3).
Уравнение цепи с НИ, обладающей активным сопротивлением R, имеет вид:
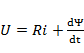 .
.
Запишем уравнение цепи с учетом известных законов изменения тока (1) и напряжения (2):
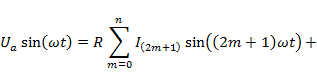
![]() . (4)
. (4)
Зная степень (2n+1) аппроксимирующего ВАХ выражения, зададим (n+1) значение аргумента функции синуса в выражении (4). Значения аргумента берем из интервала ]0;π/2].
Таким образом, получаем систему из (n+1) линейных уравнений. В полученной системе уравнений известны амплитуда напряжения Ua, амплитуды гармоник тока I(2m+1), значение активного сопротивления R и значение круговой частоты протекающего тока w, так как данные параметры цепи с НИ могут быть измерены в процессе испытания ЭУ.
Решая эту систему уравнений, получаем коэффициенты k(2m+1) аппроксимирующего ВАХ выражения (3):
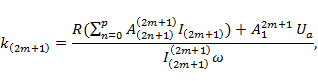
где 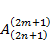 – коэффициенты (рассчитываются заранее), зависящие от номера учитываемой гармоники тока (2n+1) и номера коэффициента аппроксимирующего ВАХ выражения (2m+1), (2p+1) максимальная учитываемая гармоника тока.
– коэффициенты (рассчитываются заранее), зависящие от номера учитываемой гармоники тока (2n+1) и номера коэффициента аппроксимирующего ВАХ выражения (2m+1), (2p+1) максимальная учитываемая гармоника тока.
В таблице 1 приведены значения коэффициентов 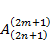 для аппроксимирующих выражений от третьей до семнадцатой степеней.
для аппроксимирующих выражений от третьей до семнадцатой степеней.
Таблица 1
Значения коэффициентов ![]() для аппроксимирующих выражений
для аппроксимирующих выражений
|
2p+1 |
k2m+1 |
A1 |
A3 |
A5 |
A7 |
A9 |
A11 |
A13 |
A15 |
A17 |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
3 |
k1 |
-5,77E-01 |
-1,15E+00 |
- |
- |
- |
- |
- |
- |
- |
|
k3 |
9,40E-02 |
1,28E-01 |
- |
- |
- |
- |
- |
- |
- |
|
|
5 |
k1 |
-5,11E-01 |
-1,43E+00 |
-2,78E-01 |
- |
- |
- |
- |
- |
- |
|
k3 |
1,53E-01 |
1,61E-01 |
-2,51E-01 |
- |
- |
- |
- |
- |
- |
|
|
k5 |
-6,10E-02 |
1,10E-02 |
8,00E-02 |
- |
- |
- |
- |
- |
- |
|
|
7 |
k1 |
-4,77E-01 |
-1,33E+00 |
-3,59E-01 |
2,40E+00 |
- |
- |
- |
- |
- |
|
k3 |
1,73E-01 |
2,01E-01 |
-3,86E-01 |
-1,28E+00 |
- |
- |
- |
- |
- |
|
|
k5 |
-6,90E-02 |
1,40E-02 |
1,10E-01 |
9,80E-02 |
- |
- |
- |
- |
- |
|
|
k7 |
-4,20E-05 |
-4,00E-05 |
7,00E-06 |
-2,25E-04 |
- |
- |
- |
- |
- |
|
|
9 |
k1 |
-4,21E-01 |
-1,29E+00 |
-2,95E-01 |
2,11E+00 |
5,31E-01 |
- |
- |
- |
- |
|
k3 |
1,51E-01 |
1,76E-01 |
-3,43E-01 |
-1,28E+00 |
1,26E-01 |
- |
- |
- |
- |
|
|
k5 |
-6,30E-02 |
1,10E-02 |
9,10E-02 |
9,80E-02 |
4,00E-03 |
- |
- |
- |
- |
|
|
k7 |
-3,90E-05 |
-3,50E-05 |
6,00E-06 |
-2,13E-04 |
2,10E-05 |
- |
- |
- |
- |
|
|
k9 |
-1,20E-07 |
2,30E-07 |
1,40E-07 |
3,00E-07 |
2,00E-07 |
- |
- |
- |
- |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
11 |
k1 |
-3,87E-01 |
-1,21E+00 |
-2,98E-01 |
2,40E+00 |
5,31E-01 |
3,78E-01 |
- |
- |
- |
|
k3 |
1,43E-01 |
2,01E-01 |
-3,86E-01 |
-1,28E+00 |
1,26E-01 |
5,90E-01 |
- |
- |
- |
|
|
k5 |
-5,70E-02 |
1,40E-02 |
1,10E-01 |
9,80E-02 |
4,00E-03 |
2,00E-03 |
- |
- |
- |
|
|
k7 |
-2,10E-05 |
-3,10E-05 |
5,00E-06 |
-4,12E-04 |
2,60E-05 |
1,20E-05 |
- |
- |
- |
|
|
k9 |
-9,00E-08 |
1,90E-07 |
1,70E-07 |
2,41E-07 |
8,90E-07 |
1,40E-07 |
- |
- |
- |
|
|
k11 |
-4,00E-08 |
-2,00E-08 |
-1,20E-08 |
2,40E-08 |
4,00E-08 |
5,10E-08 |
- |
- |
- |
|
|
13 |
k1 |
-2,57E-01 |
-1,11E+00 |
-1,78E-01 |
1,49E+00 |
8,13E-01 |
-1,82E-01 |
8,91E-01 |
- |
- |
|
k3 |
1,03E-01 |
3,11E-01 |
-3,16E-01 |
-2,01E+00 |
1,16E-01 |
4,48E-01 |
3,21E-01 |
- |
- |
|
|
k5 |
-6,00E-02 |
1,12E-02 |
1,44E-01 |
9,71E-02 |
3,21E-03 |
1,90E-03 |
7,30E-02 |
- |
- |
|
|
k7 |
-1,11E-05 |
-4,54E-05 |
4,65E-06 |
-5,05E-04 |
1,62E-05 |
3,40E-05 |
7,80E-06 |
- |
- |
|
|
k9 |
-9,11E-08 |
2,17E-07 |
1,90E-07 |
1,99E-07 |
7,81E-07 |
2,04E-07 |
1,10E-07 |
- |
- |
|
|
k11 |
-4,67E-08 |
-2,90E-08 |
-2,10E-08 |
3,17E-08 |
3,95E-08 |
4,98E-08 |
4,20E-07 |
- |
- |
|
|
k13 |
-2,30E-09 |
1,30E-08 |
4,70E-08 |
7,30E-10 |
5,30E-10 |
8,90E-11 |
9,30E-11 |
- |
- |
|
|
15 |
k1 |
-3,07E-01 |
-9,55E-01 |
-1,53E-01 |
1,28E+00 |
6,99E-01 |
-1,57E-01 |
7,66E-01 |
1,14E+00 |
- |
|
k3 |
8,86E-02 |
2,67E-01 |
-2,72E-01 |
-1,73E+00 |
9,98E-02 |
3,85E-01 |
2,76E-01 |
4,76E-02 |
- |
|
|
k5 |
-5,16E-02 |
9,63E-03 |
1,24E-01 |
8,35E-02 |
2,76E-03 |
1,63E-03 |
6,28E-02 |
7,29E-02 |
- |
|
|
k7 |
-9,55E-06 |
-3,90E-05 |
4,00E-06 |
-4,34E-04 |
1,39E-05 |
2,92E-05 |
6,71E-06 |
-3,88E-05 |
- |
|
|
k9 |
-7,83E-08 |
1,87E-07 |
1,63E-07 |
1,71E-07 |
6,72E-07 |
1,75E-07 |
9,46E-08 |
2,07E-06 |
- |
|
|
k11 |
-4,02E-08 |
-2,49E-08 |
-1,81E-08 |
2,73E-08 |
3,40E-08 |
4,28E-08 |
3,61E-07 |
7,72E-08 |
- |
|
|
k13 |
-1,98E-09 |
1,12E-08 |
4,04E-08 |
6,28E-10 |
4,56E-10 |
7,65E-11 |
8,00E-11 |
1,05E-07 |
- |
|
|
k15 |
4,21E-08 |
5,50E-08 |
1,15E-07 |
-3,02E-08 |
-3,84E-08 |
-4,96E-08 |
-4,20E-07 |
1,32E-07 |
- |
|
|
17 |
k1 |
-2,70E-01 |
-8,40E-01 |
-1,35E-01 |
1,13E+00 |
6,15E-01 |
-1,38E-01 |
6,74E-01 |
1,00E+00 |
1,26E+00 |
|
k3 |
7,80E-02 |
2,35E-01 |
-2,39E-01 |
-1,52E+00 |
8,78E-02 |
3,39E-01 |
2,43E-01 |
4,19E-02 |
8,59E-02 |
|
|
k5 |
-4,54E-02 |
8,47E-03 |
1,09E-01 |
7,35E-02 |
2,43E-03 |
1,43E-03 |
5,53E-02 |
6,42E-02 |
7,51E-02 |
|
|
k7 |
-8,40E-06 |
-3,43E-05 |
3,52E-06 |
-3,82E-04 |
1,22E-05 |
2,57E-05 |
5,90E-06 |
-3,41E-05 |
-2,91E-05 |
|
|
k9 |
-6,89E-08 |
1,65E-07 |
1,43E-07 |
1,50E-07 |
5,91E-07 |
1,54E-07 |
8,32E-08 |
1,82E-06 |
2,04E-06 |
|
|
k11 |
-3,54E-08 |
-2,19E-08 |
-1,59E-08 |
2,40E-08 |
2,99E-08 |
3,77E-08 |
3,18E-07 |
6,79E-08 |
8,22E-08 |
|
|
k13 |
-1,74E-09 |
9,86E-09 |
3,56E-08 |
5,53E-10 |
4,01E-10 |
6,73E-11 |
7,04E-11 |
9,24E-08 |
1,03E-07 |
|
|
k15 |
3,70E-08 |
4,84E-08 |
1,01E-07 |
-2,66E-08 |
-3,38E-08 |
-4,36E-08 |
-3,70E-07 |
1,16E-07 |
1,45E-07 |
|
|
k17 |
8,62E-08 |
9,88E-08 |
1,90E-07 |
-6,10E-08 |
-7,73E-08 |
-9,93E-08 |
-8,40E-07 |
1,59E-07 |
1,87E-07 |
Продемонстрируем работу метода измерения ВАХ ЭУ, проведя вычислительный эксперимент. Используем в качестве модели ЭУ схему, построенную при помощи пакета MicroCap (рис. 1).
Для демонстрации в модель закладывается ВАХ магнитопровода материала 3100B, у которого заданы два варианта зазора 0,4 и 0,9 мм, что приводит к разному наклону ВАХ.
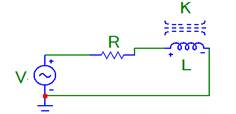
Рис. 1. Модель ЭУ.
Модель ЭУ содержит последовательно соединенные НИ L с количеством витков 95, и активное сопротивление R, равное 0,15 и 0,1 Ом, для указанных выше зазоров соответственно. К ЭУ подключен источник синусоидального напряжения V частотой 50 Гц и амплитудой Ua, равной 1,65 и 1,7 В, для указанных выше зазоров соответственно.
На рисунках 2 и 3 показаны напряжение и ток для выбранных зазоров.
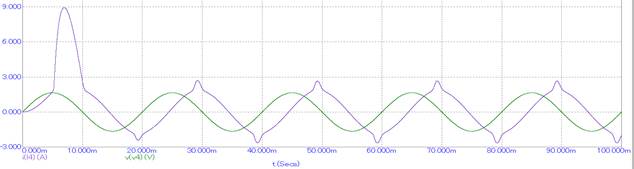
Рис. 2. Напряжение и ток при зазоре 0,4 мм.
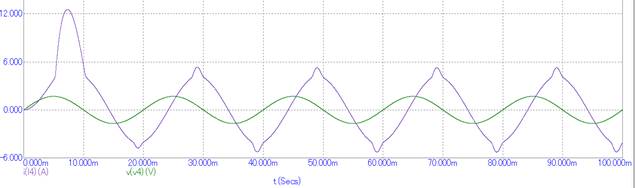
Рис. 3. Напряжение и ток при зазоре 0,9 мм.
Полученные ВАХ ЭУ для различных зазоров и учитываемых (номера указаны в скобках) гармоник тока представлены на рисунке 4.
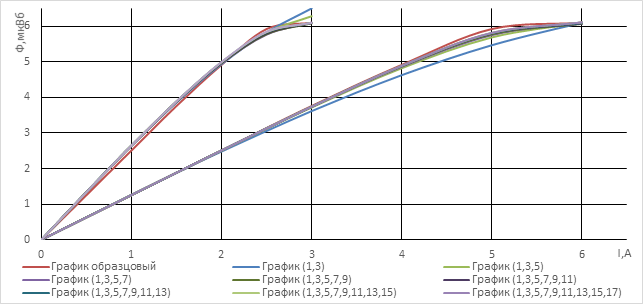
Рис. 4. ВАХ ЭУ при различных значениях зазора магнитопровода.
Рассчитаны погрешности измерения ВАХ при учете различного количества гармоник тока, результаты приведены на рисунке 5 и в таблице 2.
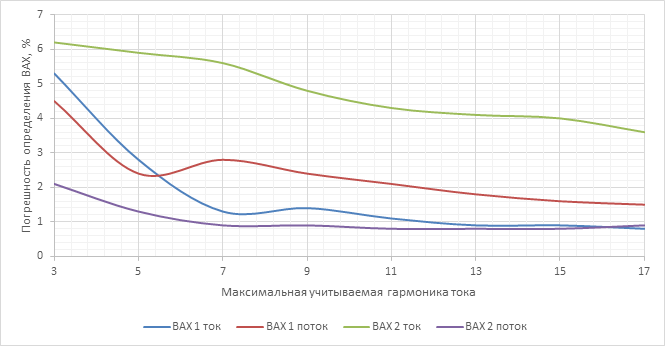
Рис. 5. Зависимость погрешности измерения от номера максимальной учитываемой гармоники тока.
Таблица 2
Погрешности определения ВАХ
|
Максимальная учитываемая гармоника тока |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
17 |
||
|
Погрешность, % |
ВАХ 1 |
i |
5,3 |
2,8 |
1,3 |
1,4 |
1,1 |
0,9 |
0,9 |
0,8 |
|
ψ |
4,5 |
2,4 |
2,8 |
2,4 |
2,1 |
1,8 |
1,6 |
1,5 |
||
|
ВАХ 2 |
i |
6,2 |
5,9 |
5,6 |
4,8 |
4,3 |
4,1 |
4,0 |
3,6 |
|
|
ψ |
2,1 |
1,3 |
0,9 |
0,9 |
0,8 |
0,8 |
0,8 |
0,9 |
||
Для определения требуемого количества гармоник тока, используемых для получения уравнения аппроксимации ВАХ, используем известный подход [3].
Будем последовательно увеличивать количество гармоник тока и контролировать изменение остаточной дисперсии:
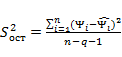 ,
,
где n – количество точек, в которых измерялись образцовые значения потока ![]() , q – количество используемых гармоник тока,
, q – количество используемых гармоник тока, ![]() - полученные значения потокосцепления.
- полученные значения потокосцепления.
Момент прекращения добавления гармоник тока определен путем проверки гипотезы об отсутствии различия остаточных дисперсий ![]() и
и ![]() . Для этого использован критерий Фишера, в соответствии с которым расчетное значение определяется по формуле:
. Для этого использован критерий Фишера, в соответствии с которым расчетное значение определяется по формуле:
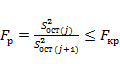 ,
,
где Fкр – критическое значение критерия Фишера для числа степеней свободы ![]() и
и ![]() .
.
Результаты для уровня значимости α = 5% представлены в таблице 3.
Таблица 3
Выбор степени полинома для различных ВАХ
|
|
2p+1 |
|
p |
f1 |
f2 |
|
|
|
ВАХ 1 |
3 |
0,091 |
2 |
18 |
16 |
- |
- |
|
5 |
0,022 |
3 |
18 |
15 |
4,09 |
2,39 |
|
|
7 |
0,0081 |
4 |
18 |
14 |
2,75 |
2,44 |
|
|
9 |
0,0031 |
5 |
18 |
13 |
2,67 |
2,51 |
|
|
11 |
0,0012 |
6 |
18 |
12 |
3,00 |
2,6 |
|
|
13 |
0,00072 |
7 |
18 |
11 |
1,43 |
2,71 |
|
|
ВАХ 2 |
3 |
0,063 |
2 |
18 |
16 |
- |
- |
|
5 |
0,021 |
3 |
18 |
15 |
3,00 |
2,39 |
|
|
7 |
0,0084 |
4 |
18 |
14 |
2,50 |
2,44 |
|
|
9 |
0,0058 |
5 |
18 |
13 |
1,45 |
2,51 |
Исходя из полученных результатов можно сказать, что для первой ВАХ требуется использовать пять нечетных гармоник тока, а для второй ВАХ три.
Вывод
Подводя итог, можно утверждать, что предложенный метод измерения вебер-амперной характеристики, основанный на решении обратной задачи МГБ, позволяет получить характеристику ЭУ с приемлемой точностью.
Статья подготовлена с использованием оборудования ЦКП «Диагностика и энергоэффективное электрооборудование» ЮРГПУ(НПИ).
Рецензенты:
Нагай В.И., д.т.н., профессор кафедры «Электрические станции и электроэнергетические системы», ФГБОУ ВПО «Южно-Российский государственный политехнический университет (НПИ) имени М.И. Платова, г. Новочеркасск.
Горбатенко Н.И., д.т.н., профессор кафедры «Информационные и измерительные системы и технологии», ФГБОУ ВПО «Южно-Российский государственный политехнический университет (НПИ) им. М.И. Платова, г. Новочеркасск.
Библиографическая ссылка
Ланкин А.М., Ланкин М.В., Наракидзе Н.Д. МЕТОД ИЗМЕРЕНИЯ ВЕБЕР – АМПЕРНОЙ ХАРАКТЕРИСТИКИ БАЗИРУЮЩИЙСЯ НА РЕШЕНИИ ОБРАТНОЙ ЗАДАЧИ МГБ // Современные проблемы науки и образования. 2014. № 4. ;URL: https://science-education.ru/ru/article/view?id=13942 (дата обращения: 06.03.2026).
DOI: https://doi.org/10.17513/spno.2014.4.118-13942



