Социально-экономическое и маркетинговое наблюдение за доходами населения, в частности оценка динамики структуры распределения населения по уровням дохода, особенно в сочетании с изменениями в структуре потребления, организуется, как правило, с применением выборочных исследований. В рамках разработанного автором Метода актуализации квазистационарного массива (МАКМ) [5] в моменты времени ti по результатам выборочных опросов формируются уменьшенные модели генеральной совокупности – массивы Ai (базовые) или ai (массивы актуализации), а на их основе в свою очередь строятся ряды распределения населения по уровням дохода, дифференцированные по социально-демографическим признакам Ri. Очевидно, что при этом каждый раз требуется оценивать репрезентативность массивов ai.
Репрезентативность ai необходимо оценивать относительно генеральной совокупности N, поскольку Ri должен представлять собой распределение всего населения территориально-административной единицы по уровням доходов. Для этого автор предлагает:
- использовать принцип оценки репрезентативности, применяемый статистикой семейных бюджетов, то есть оценить расхождения данных массивов ai с имеющейся официальной социально-демографической информацией;
- с целью проверки репрезентативности по распределению применить согласно [2, с. 461] свободный от параметров критерий Уилкоксона, который позволяет проверить, относятся ли массивы Ai и ai к одной генеральной совокупности N, то есть к населению рассматриваемой административной единицы;
- дополнительно проверить статистическую гипотезу о равенстве средних внутригрупповых дисперсий [9, с. 197-198], рассчитанных по данным Ai и ai, при этом в случае если массивы Ai и ai есть выборки из N, то величина их средних внутригрупповых дисперсий должна быть типична (близка), фактически это означает, что точность данных Ai и ai адекватна.
Сопоставление данных ai с данными официальной статистики реально производить по половозрастной структуре населения. Если отклонение долей населения по полу и среднему возрасту в каждом случае не превышает 5%-ный барьер, принятый в бюджетной статистике [7, с. 16, 18, 30], то результат актуализации можно считать репрезентативным по половозрастной структуре.
Для признания актуализации (массива ai) репрезентативной в целом рассмотрим особенности применения статистических гипотез, указанных выше.
Поскольку критерий Уилкоксона предназначен для сопоставления показателей, измеренных в двух разных условиях на одной и той же выборке испытуемых, и подразумевает упорядочивание величин, а предметом исследования (показателем) выступают доходы граждан, выраженные в рублях и зафиксированные в Ai и ai, последние необходимо привести к сопоставимому виду. Несопоставимость доходов возникает в связи с тем, что периоды формирования базового массива и массива актуализации различны, а в экономике с течением времени, вследствие таких явлений, как инфляция, существенные колебания курсов валют в связи с высокой зависимостью национальной экономики от глобальных рынков и др., изменяется покупательная способность рубля.
В качестве вариантов приведения доходов к сопоставимому виду можно рассматривать несколько приемов – исчисление приведенных к рублям доходов в бюджетах прожиточного минимума (БПМ) путем деления дохода на стоимостное выражение БПМ, как это предложено в [4, с. 74, 76], или в твердой иностранной валюте. Однако автор считает, что применение таких методов пересчета доходов для использования критерия Уилкоксона не оправдано по следующим причинам: в условиях возможного изменения состава и норм потребления продуктов, входящих в БПМ (потребительской корзины), как в большую, так и в меньшую сторону, а также в связи с неравномерным изменением доходов граждан вслед за динамикой курса основных валют, исчисление доходов населения в указанных единицах ведет к сложно прогнозируемому смещению центра распределений доходов в ai относительно Ai и тем самым к несопоставимости данных. В этой связи имеется возможность выравнивания таких данных на соответствующие расчетные величины средних доходов по формуле средней арифметической, определяемой по элементам Ai и ai соответственно:
Д*=Д/Дср , (1)
где Д* - выровненное значение дохода индивида, Д - среднедушевой доход индивида, зафиксированный в Ai и ai, Дср - средний доход по массивам Ai и ai соответственно.
Такой прием позволяет расположить все элементы массивов относительно центров распределений так, что индивиды, получающие доходы, близкие к среднему, в обоих массивах будут располагаться к значению выровненного дохода, близкому к единице. Далее проводится упорядочивание выровненных значений обоих массивов и подсчет полного количества инверсий U. При этом если абсолютное значение U-n1n2/2 ≤ Ua, где n1n2 - произведение числа элементов Ai и ai, а Ua - критическое значение числа инверсий, то гипотезу о равенстве распределений доходов в базовом массиве и массиве актуализации не отвергают. Это свидетельствует о том, что элементы Ai и ai являются частью единой совокупности N и актуализация является репрезентативной не только по отношению к Ai, но также и к генеральной совокупности N. В этом случае будем считать массив актуализации ai репрезентативным по распределению по отношению к генеральной совокупности.
В работе Е.М. Четыркина и И.Л. Калихмана [9, с. 197] отмечены следующие возможности применения задачи проверки гипотезы о равенстве двух дисперсий для решения практических задач: при анализе стабильности производственного процесса до и после введения технического новшества (колеблемость размеров деталей измеряется с помощью квадратического отклонения), при изучении степени однородности двух совокупностей в отношении какого-либо признака (квалификации рабочих, стажа, персонала и др.), при изучении качества измерительных приборов и т.п. В методе актуализации квазистационарного массива автор предлагает применить рассматриваемую гипотезу для сравнения точности исследований при формировании базовой и актуализирующей совокупностей. Отметим, что с указанной целью не могут быть использованы ни формулы общей (2), ни межгрупповой дисперсий (3), приведенные в [9, с. 107]:
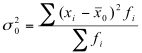 (2)
(2)
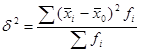 (3)
(3)
Причина тому в высокой дифференциации доходов населения, при этом чем сильнее дифференциация, тем выше вариация доходов в совокупности. В условиях нестабильных рынков дифференциация доходов населения с течением времени усиливается, поэтому сравнивать совокупности по межгрупповой дисперсии (2), которая отражает вариацию изучаемого признака под влиянием признака-фактора, положенного в основу группировки, будет неверным. Под признаком-фактором в данном случае понимается доход индивидов, на основании величины которого субъекты исследований распределяются по семи уровням доходов [6]. По этой же причине на основании закона сложения вариаций не подходит и формула общей дисперсии (3). Отсюда для сравнения качества (точности) исследований в базовом массиве и при актуализации будем использовать среднюю внутригрупповых дисперсий, определяемую по формуле (4), приведенную в [9, с. 107] и отражающую случайную вариацию в каждой из 7 рассматриваемых групп от «бедных» до «богатых» и соответствующих им уровней дохода.
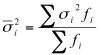 (4)
(4)
Здесь σi2 - внутригрупповая дисперсия i-й группы, определяется по аналогии с (3) для каждого уровня доходов в отдельности, ¦i - численность i-й группы.
Случайная вариация возникает во многом под влиянием других, не учитываемых факторов, и зависит от доходов населения лишь частично, то есть в пределах вариаций, определяемых разными уровнями доходов со следующей закономерностью - чем шире диапазон возможных значений доходов в некотором уровне, тем большая дисперсия возможна. Так, внутригрупповая дисперсия в группе «бедных» должна быть заведомо ниже, чем в группе «состоятельных» при достаточно большой численности этих групп, так как величина 1-го уровня «Бедные» составляет 0,7 БПМ, а величина 6-го уровня «Состоятельные» - 1,8 БПМ. Поскольку границы уровней доходов, выраженные в БПМ, во времени зафиксированы, влияние величины доходов на среднюю внутригрупповых дисперсий будем считать равновеликим для базового периода и периода актуализации.
Итак, проверим гипотезу H0 о равенстве средних внутригрупповых дисперсий, рассчитанных по данным базового массива и массива актуализации. Учитывая, что дисперсии генеральной совокупности, которую отражают данные массивы, являются неизвестными, воспользуемся их оценкой - выборочными дисперсиями S2A и S2a. В их расчете используем выровненные на величину внутригрупповых средних данные. Для сравнения S2A и S2a рассмотрим величину F*=S2A/S2a, если S2A>S2a , и F= S2a/S2A в противном случае. Если F* близко к единице, то дисперсии близки друг другу.
По таблице распределения Фишера-Снедекора при a=0,05 и nA=nA-1 и na=na-1, где nA и na - численности базового и актуализирующего массивов, найдем значение Fa. В случае если Fa³F, то гипотеза H0 не отвергается и точность исследований при актуализации будем считать равной точности исследований при формировании базового массива, а совокупности Ai и ai однородными. Поскольку массив Ai по определению является репрезентативной моделью генеральной совокупности, а массив ai соответствует по точности исследований Ai, то будем считать, что массив актуализации ai точно представляет генеральную совокупность и является репрезентативным по точности.
Таким образом, в случае удовлетворения данных актуализации трем критериям - репрезентативности по половозрастной структуре, по распределению и по точности, будем считать массив актуализации ai репрезентативным в целом по отношению к генеральной совокупности N.
Установив репрезентативность ai в целом, возможно оценить среднюю ошибку актуализации при построении ряда распределения. Для этого воспользуемся формулой средней ошибки типической выборки mw, используемой при бесповторном отборе и приведенной в [9, с. 129]:
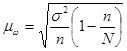 (5)
(5)
Здесь n - фактическая конечная численность достигнутых элементов актуализации (после первичной обработки с учетом исключенных из рассмотрения), N - численность населения административной единицы (генеральной совокупности N). В качестве дисперсии (σ2) для расчета средней ошибки актуализации используем формулу средней внутригрупповых дисперсий ![]() для доли альтернативного признака, исходя из ее особенностей, отмеченных выше. В качестве внутригрупповой дисперсии по i-му уровню используем дисперсию ωi(1-ωi), вычисляемую по доле населения, имеющего доходы на уровне i:
для доли альтернативного признака, исходя из ее особенностей, отмеченных выше. В качестве внутригрупповой дисперсии по i-му уровню используем дисперсию ωi(1-ωi), вычисляемую по доле населения, имеющего доходы на уровне i:
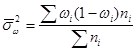 (6)
(6)
Согласно МАКМ в случае если 2μω≤0,0500 - будем считать актуализацию успешной, и согласно МАКМ может быть построен ряд распределения населения Ri по уровням доходов, дифференцированный по социально-экономическим признакам.
Распространение данных Ri на генеральную совокупность может быть осуществлено методом прямого пересчета, приведенным в [9, с. 138].
Перед формированием Ri для использования в практических целях количественная оценка актуализации должна быть дополнена экспертной по следующим причинам:
- в силу имеющих место недостатков информации государственных органов статистики, на базе которых формируется Ai, возможный неточный учет высокодоходных групп населения должен быть компенсирован путем проведения экспертных опросов;
- оценка доходов, скрываемых при проведении обследований от интервьюеров, а также доходов, не подвергнутых учету, может быть проведена экспертным путем.
Согласно работам Бешелева С.Д., Гурвича Ф.Г. [1], Беляевского И.К., Кулагиной Г.Д., Короткова А.В. [8], поскольку непосредственную информацию о достоверной численности указанной группы получить крайне сложно, для оценки адекватности Ri в части «богатых» может быть использован Дельфи-метод. С этой целью привлекаются эксперты – анонимные респонденты, входящие в группу населения по уровню доходов «богатые». Численность и порядок проведения экспертного опроса устанавливается согласно [1, с. 48-50]. В качестве вспомогательного материала при проведении опроса могут использоваться данные столбцов 1-3 таблицы 1, разработанной автором с учетом результатов исследования Н.М. Давыдовой и Н.Н. Седовой [3]. В основе разработки имущественного признака использован принцип предельного соответствия доходов и расходов домохозяйств. Промежуточные результаты помещаются в столбец 4 таблицы 1.
Таблица 1.
Социальные и имущественные признаки группы населения «богатые»
|
Месячный среднедушевой доход, БПМ (принято эвристически) |
Социальный статус и положение в обществе |
Отличия (имущественный признак/ особенности потребления) |
Оценка кол-ва человек |
|
5,4 – 13,3 БПМ
|
Руководители-собственники малых и средних работающих предприятий, менеджеры среднего звена на крупных предприятиях прибыльных отраслей, владельцы нескольких торговых точек и т.п. |
Импортный автомобиль среднего класса, приобретенное жилье в новостройках экономического класса |
Q1 |
|
13,3 – 20,0 БПМ
|
Менеджеры верхнего звена крупных предприятий, собственники средних предприятий |
Приобретенное жилье в новостройках бизнес-класса. Дорогие импортные автомобили. Отдых за границей несколько раз в год. Хорошее образование. Платные медицинские услуги в ведущих клиниках |
Q2 |
|
20,0 – 29,3 БПМ
|
Руководители-собственники средних высокодоходных предприятий |
Европейский тип потребления. Импортные автомобили премиум-класса. Несколько личных а/м в семье. Владение одной или несколькими квартирами, в том числе премиум-класса. Платное образование детей за рубежом |
Q3 |
|
29,3 – 66,6 БПМ
|
Руководители-собственники крупных предприятий, менеджеры высшего звена прибыльных крупных предприятий |
Владение одной или несколькими дорогими квартирами премиум-класса. Импортные автомобили премиум-класса. Наличие загородного коттеджа. VIP-обслуживание. Платное образование детей за рубежом |
Q4 |
|
от 66,6 БПМ и выше
|
Руководители-собственники и топ-менеджеры крупнейших предприятий |
Спецобслуживание. Персональная охрана. Недвижимость за рубежом |
Q5 |
По результатам опроса осуществляется суммирование оценок Qi по рассмотренным категориям и вычисление экспертной оценки Q доли «богатых» в генеральной совокупности. В случае если экспертная доля Q не превышает установленной в результате актуализации по группе населения «богатые», то Ri признается пригодным для использования, в том числе по «богатым», и может быть предоставлен конечным потребителям. В противном случае требуется осуществить коррекцию Ri с увеличением доли «богатых» и соответствующим уменьшением доли ближайшей группы «состоятельных». При коррекции установленная в результате актуализации социальная структура группы «богатые» сохраняется путем пропорционального распределения дополнительной численности по детализированным группам.
Рецензенты:
Захаров Н.Л., д.с.н., профессор, профессор кафедры социологии и управления персоналом Санкт-Петербургского государственного экономического университета, г. Санкт-Петербург.
Шелонаев С.И., д.с.н., профессор, заведующий кафедрой журналистики и медиатехнологий СМИ Северо-Западного института печати Санкт-Петербургского государственного университета технологии и дизайна, г. Санкт-Петербург.
Библиографическая ссылка
Игнатенко В.О. МЕТОДИКА ОЦЕНКИ РЕПРЕЗЕНТАТИВНОСТИ И ДОПОЛНЕНИЯ РЕЗУЛЬТАТОВ ВЫБОРОЧНЫХ ИССЛЕДОВАНИЙ ДОХОДОВ НАСЕЛЕНИЯ // Современные проблемы науки и образования. 2014. № 4. ;URL: https://science-education.ru/ru/article/view?id=13836 (дата обращения: 06.03.2026).



