Введение. Оперативный контроль коллекторских характеристик прискважинной зоны позволяет оптимизировать процессы эксплуатации газовых месторождений и тем самым увеличивать продолжительность и эффективность эксплуатации скважин [4, 5]. Для исследования коллекторских характеристик призабойной зоны пластов используются различные гидродинамические, геофизические, термогидродинамические методы. В работе для оценки коллекторских характеристик призабойной зоны временно остановленных газовых скважин предлагается использовать альтернативный метод – метод опрессовки.
Метод заключается в следующем: выбирается исследуемый участок скважины, закрывается этот участок с двух концов и резко повышается давление на этом участке. Далее исследуется динамика релаксации давления в скважине за счет фильтрации газа в окружающую пористую среду. Темп релаксации давления зависит от коллекторских характеристик окружающей пористой породы. Поэтому по времени релаксации давления можно судить, например, о величине коэффициента проницаемости породы вокруг скважины.
Преимущество этого метода заключается в том, что он является экспресс методом, т.е. за короткое время можно оценить параметры призабойной зоны. Метод опрессовки является наиболее привлекательным для использования в месторождениях с низкой проницаемостью.
В работе исследование процесса релаксации давления в скважине, окруженной насыщенной газом пористой средой, после опрессовки сведено к решению нелинейных интегральных уравнений. Проведен анализ зависимости периода полувосстановления давления в скважине от коллекторских характеристик окружающей пористой породы. Периодом полувосстановления давления будем называть промежуток времени, в течение которого разница между значениями давлений в скважине и пористой среде снижается в два раза от начальной разницы. Понятие период полувосстановления давления используется в работах [3, 6] при исследовании коллекторских характеристик пористой среды, насыщенной жидкостью, методом опрессовки полости.
1. Основные уравнения. Пусть в исходном состоянии (
) давление газа во всем пористом пласте вокруг скважины постоянно и равно 
, а сама скважина (рис. 1) заполнена газом. В момент времени 
в скважину дополнительно вводится газ, и давление в ней мгновенно достигает значения 
. Далее за счет фильтрации газа в окружающее пористое пространство давление в скважине стремится к значению .
При описании исследуемого процесса скелет пористой среды будем считать несжимаемым и однородным, а коэффициент вязкости газа не зависящим от температуры и давления. В рамках выше изложенных допущений, учитывая, что изменение массы газа в скважине происходит только за счет фильтрации через стенки скважины в окружающую пористую среду, запишем уравнение сохранения массы газа в следующем виде:
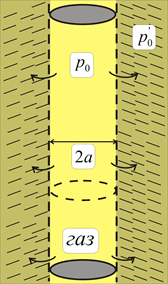
Рис. 1. Схематическое изображение исследуемого участка скважины
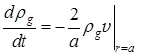, (1)
где 
– радиус скважины; 
– плотность газа; 
– скорость фильтрации газа через стенки скважины.
Давление в окружающей скважину пористой среде будем описывать с помощью нелинейного уравнения пьезопроводности [1]:
, 
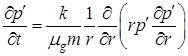. (2)
Здесь 
– коэффициент динамической вязкости газа; 
– давление газа вокруг скважины; 
и 
– коэффициенты пористости и проницаемости окружающей скважину пористой среды.
Учитывая, что в исходном состоянии давление газа во всем пористом пласте вокруг скважины постоянно и равно начальное условие для уравнения (2) запишем в виде:
. (3)
На стенке скважины (r = a) выполняется условие равенства давлений справа и слева
, (4)
где 
– давление внутри скважины.
Второе граничное условие для уравнения (2) имеет вид:
. (5)
Аналитическое решение нелинейного уравнения пьезопроводности общего вида для фильтрации газа (2) при условиях (3)–(5) не найдено. В работе уравнение (2) будем использовать в линеаризованном приближении. Для этого перепишем уравнение (2) в виде:
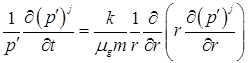, (6)
где значения показателя степени j = 1 и 2 соответствуют обычной линеаризации и линеаризации по Лейбензону [2]. Заметим, что изменение мало относительно среднего значения этой величины, поэтому коэффициент при 
в левой части уравнения (6) можно считать постоянным.
Таким образом, если во всей области течения и для всех значений t величина мало отклоняется от своего начального значения, то уравнение (6) можно переписать в виде
, 
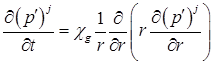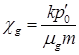, (7)
где 
– коэффициент пьезопроводности.
Для фильтрации газа в пористой среде вокруг скважины используем закон Дарси:
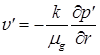, (8)
где 
– скорость фильтрации газа вокруг скважины. Используя условие непрерывности скорости на стенке скважины, для уравнения (8) можно записать:
.
Для замыкания системы уравнений (1), (7) и (8), считая, что газ является калорически совершенным, запишем связь текущих значений плотности и давления в скважине:
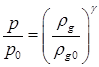, (9)
где 
– показатель политропы, 
– начальное значение плотности газа в скважине.
Подставляя в уравнение (1) величину 
из (9), получим:
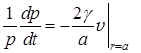(10)
Уравнение (10) связывает давление внутри скважины со скоростью фильтрации газа через ее стенки.
2. Решение задачи. Применяя принцип Дюгамеля, решение уравнения (7), удовлетворяющего условиям (3)–(5), можем записать в виде
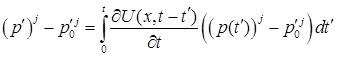, (11)
,
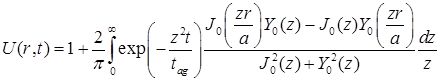где 
и 
– функции Бесселя и Неймана нулевого порядка. Используя решение (11) и закон Дарси (8), из уравнения (10) получим следующие нелинейные интегральные уравнения, описывающие эволюцию давления внутри скважины:
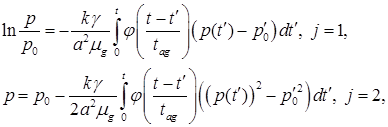(12)
.
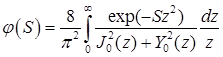В уравнениях (12) неизвестной величиной является только давление, а все остальные – это параметры жидкости, скважины и пористой среды. Решая интегральные уравнения (12) при различных значениях параметров пористой среды, можем найти зависимости динамики релаксации давления от этих параметров. Таким образом, в работе процесс оценки параметров призабойной зоны сводится к решению нелинейных интегральных уравнений. Интегральные уравнения решались численным методом. Исследовались зависимости периода полувосстановления давления в опресованной скважине от параметров пористости , коэффициента проницаемости k.
Рис. 2 иллюстрирует влияние пористости на процесс релаксации давления в скважине. По горизонтали отложено время в секундах, а по вертикали – безразмерное давление 
. Сплошные линии во всех рисунках соответствуют обычной линеаризации уравнения пьезопроводности, а пунктирные линии – линеаризации по Лейбензону. Линии 1 получены при значении 
, а линии 2 – 
. Горизонтальная тонкая пунктирная линия соответствует значению давления в момент наступления периода полувосстановления. Видно, что как весь процесс релаксации давления в скважине, так и период полувосстановления давления от пористости слабо зависит.
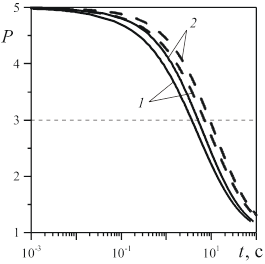
Рис. 2. Релаксация безразмерного давления в скважине при различных значениях коэффициента пористости
На рис. 3 представлена зависимость периода полувосстановления давления от коэффициента проницаемости. Из рисунка видно, что период полувосстановления давления обратно пропорционален коэффициенту проницаемости среды.
Выводы. Развита теория исследования прискважинной зоны пластов. Для оценки коллекторских характеристик призабойной зоны временно остановленных газовых скважин предлагается использовать альтернативный метод – метод опрессовки. Разработана математическая модель, описывающая процесс опрессовки скважины. Исследование процесса релаксации давления в опрессованной скважине сведено к решению нелинейных интегральных уравнений. В результате численного анализа этих уравнений установлено, что период полувосстановления давления обратно пропорционален коэффициенту проницаемости и слабо зависит от пористости среды.
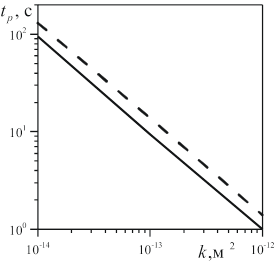
Рис. 3. Зависимости периода полувосстановления давления от коэффициента проницаемости
Работа выполнена при поддержке гранта СФ БашГУ № В14-19.
Рецензенты:
Мустафина С.А., д.ф.-м.н., профессор кафедры математического моделирования, Стерлитамакский филиал ФГБОУ ВПО «Башкирский государственный университет», Республика Башкортостан, г. Стерлитамак.
Михайлов П.Н., д.ф.-м.н., профессор кафедры алгебры, геометрии и методики обучения математике, Стерлитамакский филиал ФГБОУ ВПО «Башкирский государственный университет», Республика Башкортостан, г. Стерлитамак.
Библиографическая ссылка
Хусаинов И.Г., Хусаинова Г.Я. ИССЛЕДОВАНИЕ ПАРАМЕТРОВ ПЛАСТА МЕТОДОМ ОПРЕССОВКИ // Современные проблемы науки и образования. – 2014. – № 3. ;URL: https://science-education.ru/ru/article/view?id=13813 (дата обращения: 24.04.2024).