Цель исследования
Изменение базовой структуры параллельного манипулятора с целью улучшения конструктивных параметров манипулятора, моделирование и оценка практической значимости разработанных структур на анализе полученных данных.
Введение
Манипуляторы параллельной структуры находят все большее применения в отраслях промышленности в странах Япония, США, Китай при выполнении различных работ. Это связано с их положительными свойствами, таких как маштабируемость, хорошее соотношение полезной нагрузки к массе гибких связей манипулятора, простота конструкции и использование в качестве рабочего органа различных приспособлений (многофункциональность рабочего органа). Самой известной структурой манипулятора с гибкими звеньями является "RoboCrane"[4], предложенная Джеймсом Альбусом. Используя данную структуру манипулятора, получилось построить на юго-западе Китая гигантский радиотелескоп [5] со сферой 500 метров, что из-за своих размеров было бы сложно реализовать другим иным способом. Данная статья является продолжением работы [3] и посвящена исследованию распределения возможных силовых нагрузок на звенья манипулятора произвольной формы зоны обслуживания.
Результаты исследования и их обсуждения
Проанализируем базовую структуру манипулятора, рассмотренную в [2], кинематическую схему, которая представлена на рис 1а. Манипулятор состоит из четырех колонн, четырех тросов, которые одним из концов соединены в точке крепления груза P; вторые концы тросов, пропущенных через шкивы Ш1, Ш2, Ш3, Ш4, закрепленные на колоннах, закрепляются на барабанах Б1, Б2, Б3, Б4 соответственно. Под действием веса груза mg, закрепленного в точке P, в тросах возникают силы натяжения T1, T2, T3, T4, причем в зоне 1 вес груза распределяется между первым, вторым и третьим тросом, а в зоне 2 – между вторым, третьим и четвертым тросом. Изменение положения точки крепления груза происходит за счет изменения длин тросов при вращении барабанов мотор-редукторами М1, М2, М3, М4.
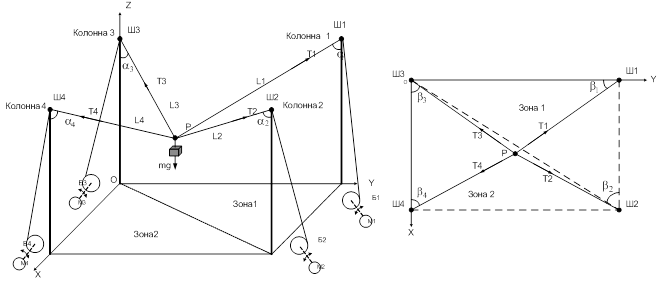 а)
а)
б)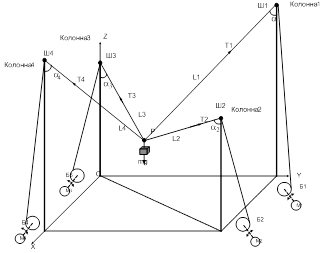
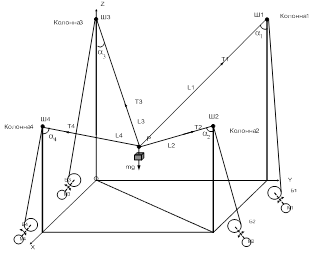 в)
в)
Рисунок 1 – Кинематическая схема манипуляторов на основе гибких звеньев, а) с одинаковой высотой колонн, б) с увеличенной высотой колонн 1 и 4, в) с увеличенной высотой колонн 1 и 3
Силы натяжения в гибких звеньях можно рассчитать путем решения систем нелинейных уравнений, расчеты коэффициентов которых приведены в [1], имеющих вид:
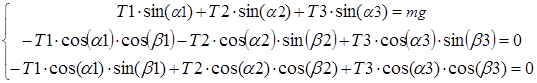 (1)
(1)
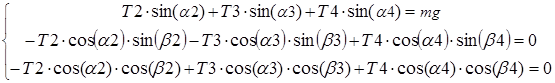 (2)
(2)
Здесь Т1-Т4 – сила натяжения тросов;
α1-α4 – зенитные углы;
β1- β4 – азимутальные углы;
mg – вес груза.
Коэффициенты при неизвестных (синусы и косинусы углов) рассчитываются методами элементарной геометрии и зависят от расположения точки P (груза) в пространстве рабочей зоны.
Для оценки нагруженности звеньев манипулятора разработана компьютерная модель с использованием среды программирования Matlab. Для сравнения с базовой структурой манипулятора будут рассмотрены две структуры, с увеличенными колонами, представленные на рисунке 1б и 1в. Первая – с увеличенными колонами 1 и 3 (рисунок 1б), вторая структура – с увеличенными колонами 1 и 3 (рисунок 1в).
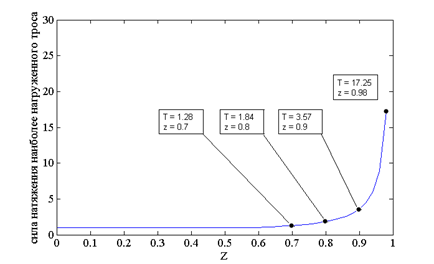
Для оценки эффективности работы рассматриваемых структур манипуляторов, с помощью разработанной компьютерной модели, были получены графики позволяющие, представить зависимость наиболее нагруженного троса при перемещении груза в плоскости ![]() от высоты плоскости
от высоты плоскости ![]() . Результат моделирования представлен на рисунке 2. Результат моделирования, был получен при следующих входных параметрах компьютерной модели:
. Результат моделирования представлен на рисунке 2. Результат моделирования, был получен при следующих входных параметрах компьютерной модели:
- для базовой структуры Ш1(1;0;1), Ш2(1;1;1), Ш3(0;0;1), Ш4(0;1;1), mg =1;
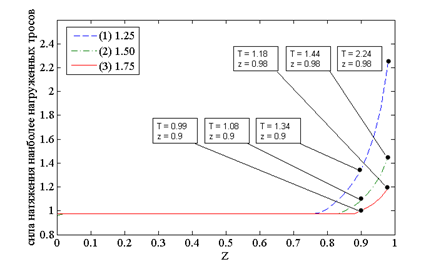
- для структуры с увеличенными колоннами 1 и 4 Ш1(1;0;V), Ш2(1;1;1), Ш3(0;0;1), Ш4(0;1;V), mg =1; (где величина V принимает значение 1.25; 1.5 и 1.75.)
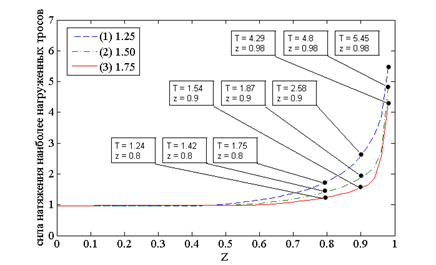
- для структуры с увеличенными колоннами 1 и 3 Ш1(1;0;V), Ш2(1;1;1), Ш3(0;0;V), Ш4(0;1;1), mg =1; (где величина V принимает значение 1.25; 1.5 и 1.75.)
 а)
а)
 б)
б)
 в)
в)
Рисунок 2 – Зависимость величины усилия наиболее нагруженного троса от значения высоты перемещаемого груза а) с одинаковой высотой колонн равной 1, б) с увеличенной высотой диагональных колонн 1 и 4, в) с увеличенной высотой колонн 1 и 3
Так же при данных входных параметров построена зависимость максимальной суммарной силы натяжения тросов при перемещении груза в плоскости ![]() от высоты плоскости
от высоты плоскости ![]() . Результат моделирования представлен на рисунке 3.
. Результат моделирования представлен на рисунке 3.
 а)
а)
 б)
б)
 в)
в)
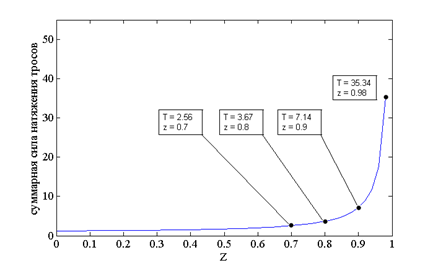
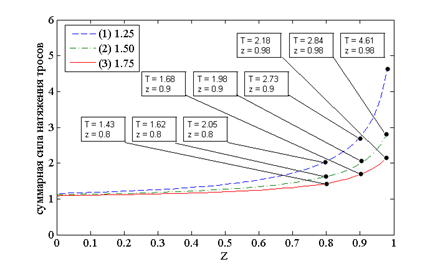
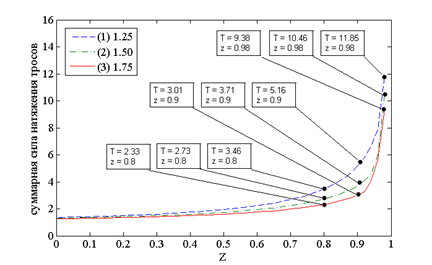
Рисунок 3 – Зависимость максимального значения уровня напряжения в элементах звеньев манипулятора от высоты перемещаемого груза а) с одинаковой высотой колонн, б) с увеличенной высотой диагональных колонн 1 и 4, в) с увеличенной высотой колонн 1 и 3
Из графиков, представленных на рисунках 2 и 3, видно, что зависимости усилия наиболее нагруженного троса и максимального значения уровня напряжения в элементах звеньев манипулятора являются между собой пропорциональными функциями. Так, кривая (рисунок 3а) отображает зависимость суммарной силы натяжения тросов манипулятора с одинаковой высотой колонн от высоты перемещаемого груза, а на рисунках 3б и 3в кривые 1, 2 и 3 – манипулятора с увеличенной высотой колонн на 1.25, 1.50 и 1.75, соответственно. Как видно из графика, увеличение диагональных колонн на 1.25 позволило существенно снизить нагрузку на звенья манипулятора. При высоте 0,9 выигрыш в суммарной силе составляет более чем в 2 раза, а при высоте 0,98 более чем в 7 раз. При увеличении колонн на 1.50 и 1.75 суммарная сила продолжает уменьшаться, и приблизительно имеют одинаковые значения. Это говорит о том, что увеличение диагональных колонн целесообразно осуществлять не более чем на 1.50. Так, увеличение колонн 1 и 3 на 1.25 также позволило снизить нагрузку на звенья манипулятора. При высоте 0,9 выигрыш в суммарной силе составляет более чем в 1,3 раза, а при высоте 0,98 – более чем в 3 раза. При увеличении колонн на 1.50 и 1.75 суммарная сила продолжает уменьшаться. Эффективность использования манипуляторов с увеличенными колонами относительно манипулятора с одинаковыми колоннами достигается только при подъеме груза выше высоты 0,7. Ниже высоты 0,7 представленные манипуляторы имеют почти одинаковые суммарные нагрузки на звенья.
Для оценки эффективности работы рассматриваемых структур манипуляторов от измененной формы зоны обслуживании при сохранении рабочего объема были получены графики, позволяющие представить зависимости наиболее нагруженного троса и максимальной суммарной силы натяжения тросов при перемещении груза в плоскости ![]() от высоты плоскости
от высоты плоскости ![]() . Результат моделирования представлен на рисунке 4. Результат моделирования был получен при следующих входных параметрах компьютерной модели:
. Результат моделирования представлен на рисунке 4. Результат моделирования был получен при следующих входных параметрах компьютерной модели:
- для базовой структуры Ш1 (2;0;1), Ш2(2;0.5;1), Ш3(0;0;1), Ш4(0;0.5;1), mg =1;
- для структуры с увеличенными колоннами 1 и 4 Ш1 (2;0;V), Ш2(2;0.5;1), Ш3(0;0;1), Ш4(0;0.5;V), mg =1; (где величина V принимает значение 1.25; 1.5 и 1.75.)
- для структуры с увеличенными колоннами 1 и 3 Ш1 (2;0;V), Ш2(2;0.5;1), Ш3(0;0;V), Ш4(0;0.5;1), mg =1; (где величина V принимает значение 1.25; 1.5 и 1.75.)
 а)
а)
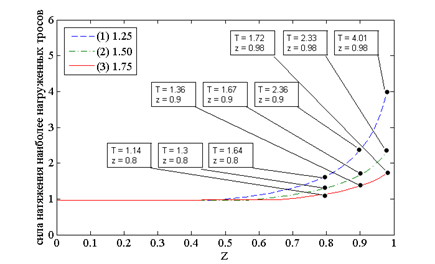 б)
б)
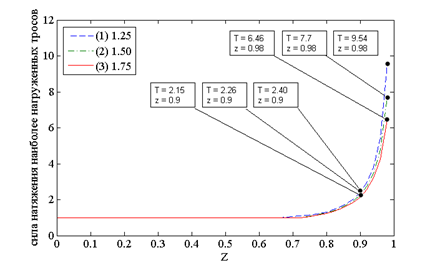 в)
в)
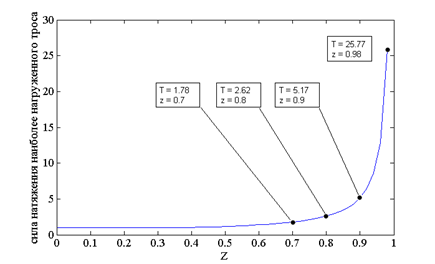
Рисунок 4 – Зависимость величины усилия наиболее нагруженного троса от значения высоты перемещаемого груза а) с одинаковой высотой колонн равной 1, б) с увеличенной высотой диагональных колонн 1 и 4, в) с увеличенной высотой колонн 1 и 3
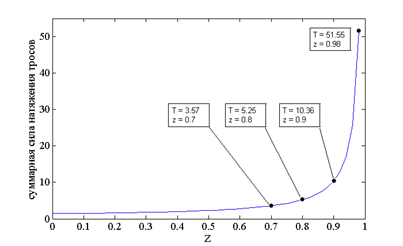 а)
а)
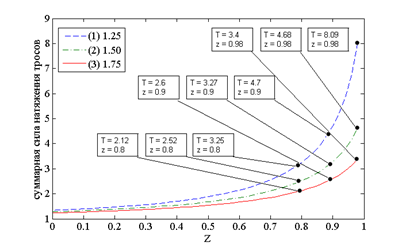 б)
б)
 в)
в)
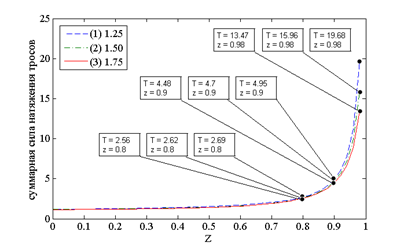
Рисунок 5 – Зависимость максимального значения уровня напряжения в элементах звеньев манипулятора от высоты перемещаемого груза а) с одинаковой высотой колонн, б) с увеличенной высотой диагональных колонн 1 и 4, в) с увеличенной высотой колонн 1 и 3
На графиках (рисунок 4 и 5), представленных выше, видно, что данная форма зоны обслуживания с размерами плоскости XOY 2x0.5 при одинаковой высоте колонн по сравнению со структурой рассмотренной ранее увеличивает нагрузку на звенья манипулятора в 1.45 раза. Однако увеличение любых двух колонн структуры также позволяет уменьшить суммарную нагрузку на звенья манипулятора, но менее эффективно по сравнению со структурой манипулятора с размерами плоскости XOY 1x1.
Выводы. Таким образом, с целью уменьшения нагрузок на звенья манипулятора были исследованы структуры манипуляторов с произвольной формой зоны обслуживания. Было установлено, что структура, имеющая размеры плоскости XOY 1x1, оказывает меньшую нагрузку на звенья манипулятора по сравнению со структурой с размерами плоскости XOY 2x0.5. Данная закономерность прослеживается и при одинаковой высоте колонн, так и при увеличенных колонн 1 и 4 и колонн 1 и 3. Так, структура 1x1 лучше структуры 2x0.5
- при одинаковой высоте колонн выигрыш в силе в 1.45 раза (z = 0.98); в 1.42 раза (z = 0.9); в 1.35 раза (z = 0.8);
- при увеличении колонн 1 и 4 на 25% выигрыш в силе в 1.74 раза (z = 0.98); в 1.74 (z = 0.9); в 1.62 (z = 0.8);
- при увеличении колонн 1 и 4 на 50% выигрыш в силе в 1.67 раза (z = 0.98); в 1.6 (z = 0.9); в 1.56 (z = 0.8);
- при увеличении колонн 1 и 4 на 75% выигрыш в силе в 1.54 раза (z = 0.98); в 1.52 (z = 0.9); в 1.5 (z = 0.8);
- при увеличении колонн 1 и 3 на 25% выигрыш в силе в 1.3 раза (z = 0.98); в 1.14 (z = 0.9); в 1.01 (z = 0.8);
- при увеличении колонн 1 и 3 на 50% выигрыш в силе в 1.52 раза (z = 0.98); в 1.27 (z = 0.9); в 1.05 (z = 0.8);
- при увеличении колонн 1 и 3 на 75% выигрыш в силе в 1.43 раза (z = 0.98); в 1.5 (z = 0.9); в 1.08 (z = 0.8);
Таким образом, структура, имеющая плоскость XOY в виде квадрата будет обладать наилучшими показателями от любой другой формы плоскости XOY. Тем самым, чем больше величина соотношений сторон OX и OY, тем больше будет нагружены звенья манипулятора. Если анализировать структуру 1 x1, то наиболее лучшими характеристиками обладает структура с увеличенными колоннами 1 и 4, так при увеличении колонн:
- на 25% выигрыш в силе в 7,6 раза (z = 0.98); в 2,6 (z = 0.9); в 1,85 (z = 0.8);
- на 50% выигрыш в силе в 12,5 раза (z = 0.98); в 3,5 (z = 0.9); в 2,3 (z = 0.8);
- на 75% выигрыш в силе в 15,9 раза (z = 0.98); в 4,11 (z = 0.9); в 2,64 (z = 0.8).
Структура с увеличенными колоннами 1 и 3:
- на 25% выигрыш в силе в 2,91 раза (z = 0.98); в 1,34 (z = 0.9); в 1,85 (z = 0.8);
- на 50% выигрыш в силе в 3,33 раза (z = 0.98); в 1,89 (z = 0.9); в 1,37 (z = 0.8);
- на 75% выигрыш в силе в 3,72 раза (z = 0.98); в 2,33 (z = 0.9); в 1,54 (z = 0.8).
Однако для данных структур существенный выигрыш наблюдается лишь при поднятии груза выше 0,8. Также сделаны выводы о том, что увеличение диагональных колонн целесообразно осуществлять не более чем на 50% для данного рассматриваемого рабочего пространства.
Данные исследования могут быть использованы при построении данной конструкции устройства перемещения груза с целью снижения силы натяжения тросов манипулятора, что в свою очередь позволит сделать эксплуатацию более надежной, экономичной и безопасной.
Рецензенты:
Привалов А.А., д.т.н., профессор кафедры «Сервис транспортных и технологических машин» Шахтинского института (филиала) ФГБОУ ВПО ЮРГПУ(НПИ) им. М.И. Платова, г.Шахты.
Плешко М.С., д.т.н., доцент, заведующий кафедрой «Энергетика и безопасность жизнедеятельности», ФГБОУ ВПО «Институт сервисного обслуживания и предпринимательства (филиал) ДГТУ», г. Шахты.
Библиографическая ссылка
Валюкевич Ю.А., Алепко А.В., Яковенко Д.М. АНАЛИЗ КОНСТРУКТИВНЫХ ПАРАМЕТРОВ МАНИПУЛЯТОРА ПАРАЛЛЕЛЬНОЙ СТРУКТУРЫ С ГИБКИМИ ЗВЕНЬЯМИ // Современные проблемы науки и образования. 2014. № 3. ;URL: https://science-education.ru/ru/article/view?id=13769 (дата обращения: 11.02.2026).



