Автоматическое обнаружение аналитических сигналов в инверсионной вольтамперометрии является ключевой задачей, убирающей субъективную составляющую при анализе вольтамперограмм и уменьшающей время анализа в целом. Кроме того, автоматизация поиска аналитических сигналов является первоочередной задачей при автоматизации процесса анализа вольтамперных кривых в целом.
Обычно, сигнал от химического элемента представлен в форме пика и представляет из себя сложную колоколообразную функцию [1] на фоне других мешающих элементов, наклона и высокочастотного шума. Правильная разметка положения пиков, а так же оценка их ширины дают важную информацию для автоматизации проведения линии остаточного тока.
На рис. 1 показана типичная картина вольтамперных кривых, полученная при определении массовых концентраций Zn, Cd, Pb, Cu в реальных пробах питьевой воды по методике [8].
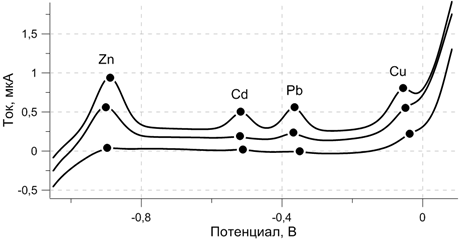
Рис. 1. Вольтамперограммы фона, пробы и пробы с добавкой (кривые, снизу вверх) полученные по методике [8]. Обозначения см. в тексте.
На рисунке изображены три вольтамперные кривые, характеризующие (снизу вверх) фон, пробу и пробу с добавкой. На каждой кривой маркерами обозначены максимумы пиков.
Выделим характерные особенности вольтамперограмм, получаемых по методу добавок в инверсионной вольтамперометрии:
- пики могут находиться на сильном наклоне линии остаточного тока (на рис.1 это пики Zn и Cu);
- пики могут перекрываться (на рис.1 это пики Cd и Pb);
- пики на фоновой кривой могут быть очень слабо выражены либо не наблюдаться в принципе (чистый фон).
Из-за наличия множества факторов во время анализа, влияющих на форму пика, кривые снимают сериями по 5-10 кривых (фона, пробы и пробы с добавкой). На рис. 2 показана серия для пробы с добавкой, состоящая из девяти вольтамперограмм полученных по методике [8].
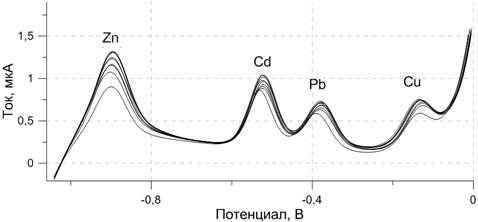
Рис. 2. Серия вольтамперограмм пробы с добавкой
Целью данной статьи является описание алгоритма автоматического поиска всех возможных пиков на вольтамперной кривой, учитывающего особенности поведения фоновой линии.
Алгоритм обнаружения пиков
В литературе описывается несколько различных эмпирических моделей, используя которые, можно аналитически описать пик, полученный методом инверсионной вольтамперометрии [1]. Для обратимых электродных процессов на ртутно-пленочном электроде в области средних толщин пленок форма пика мало отличается от симметричного пика Гаусса [4]. Для необратимых процессов, для процессов, осложненных предшествующими и последующими химическими реакциями, наблюдается отклонение формы пика от симметричности. В качестве модели несимметричного пика в [1,4] предложено использовать функцию, которая представляет собой логарифмическую модификацию абсциссы пика производной логисты.
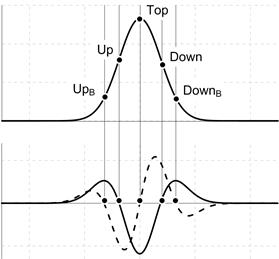
Рис. 3. Демонстрация алгоритма обнаружения центра пика: а) исходный пик, б) первая (сплошная) и вторая (штриховая) производные пика
Как симметричные, так и несимметричные пики имеют характерные точки, определяемые на основе анализа их производных [6] (рис. 3):
- вершина пика (Top). Характеризуется пересечением с нулём третьей производной из «минуса» в «плюс»;
- перегибы пика для восходящей и нисходящей ветвей (Up, Down). Характеризуются пересечением с нулём второй производной;
- пики первых боковых лепестков второй производной восходящей и нисходящей ветвей (UpB, DownB). Характеризуются пересечением с нулём третьей производной.
Обнаружение характерных точек осуществляется по смене знака 2-ой и 3-ей производных.
На рис. 4 показана функциональная схема поиска «простых» пиков (у линии остаточного тока отсутствует наклон). Назовём такие пики пиками первого рода.
В кружках блоков указан порядок производной, а стрелка показывает, с какой стороны производная пересекает ноль. Под стрелками подписано, какой характерной точке пика соответствует пересечение с нулём.
По приведённому алгоритму кривая, состоящая из n точек, сканируется на предмет последовательного выполнения условий пересечения с нулём её производных. Если все три условия последовательно выполняются, то пик считается обнаруженным.
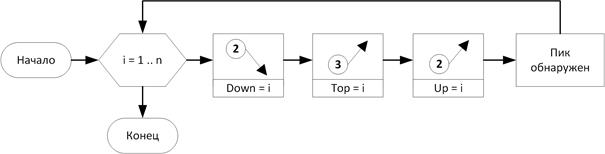
Рис. 4. Функциональная схема поиска простых пиков
После обнаружения пика необходимо проверить условие соответствия ширины пика на уровне точек перегиба:
![]() (1)
(1)
где Wmin, Wmax — минимальная и максимальная полуширина пика на уровне точек перегиба, которые находятся эмпирическим путём для конкретной методики анализа. Для методики [8] Wmin = 20 мкВ, Wmax = 150 мкВ. Расчёт граничных теоретических значений полуширин пика описан в работе [2]. Если условие не выполняется, то пик считается ложным и убирается из дальнейшего рассмотрения.
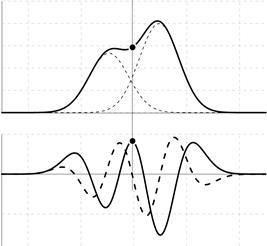
Предложенный алгоритм будет работоспособным и для частично перекрывающихся пиков (рис 5а) до тех пор, пока перестанет существовать явная точка перегиба (пересечение с нулём) нисходящей ветви первого пика и соответственно, восходящей ветви второго пика (рис 5б). Способы разделения частично перекрывающихся пиков, в приложении вольтамперометрии, было подробно рассмотрено в [5].
 а)
а) 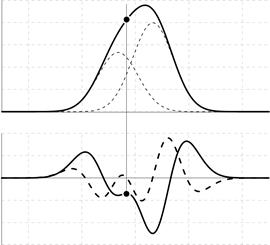 б)
б)
Рис. 5. Перекрытия двух пиков, при возможности их разделения (а) и без возможности разделения (б)
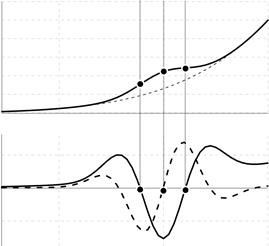
Алгоритм способен обнаруживать пик, если отсутствует локальный максимум у исходной вольтамперограммы, что проявляется при сильном наклоне и малой высоте пика (рис 6а).
 а)
а) 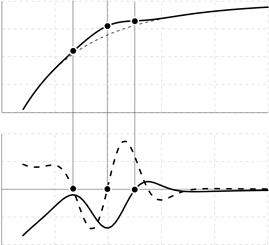 б)
б)
Рис. 6. Пики на возрастающих наклонах для случаев начальной (а) и конечной (б) ветвей вольтамперограммы
Особого рассмотрения заслуживает случай, когда пик находится на начальном возрастающем наклоне (рис. 6б, пик Zn на рис. 1). В этом случае может отсутствовать точка Up. Назовём такой пик пиком 2-го рода. Для обнаружения пика 2-го рода необходимо:
- вести поиск пиков справа налево;
- для последней найденной точки, за точкой Top, дополнительно производить поиск смены знака третьей производной с минуса на плюс.
На рис. 7 показана функциональная схема поиска пиков 1-го и 2-го родов.
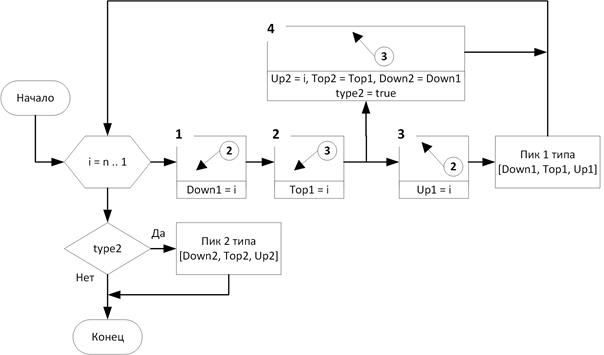
Рис. 7. Функциональная схема поиска пиков
При наличии пика первого рода схема поиска соответствует последовательности блоков 1 → 2 → 3. Если присутствует пик второго рода, то последовательность поиска будет 1 → 2 → 4, а обнаружение пика произойдёт, только если это был последний пик.
После обнаружения пика его также нужно проверить по критерию полуширины на уровне точек перегиба по выражению (1).
Выводы
Разработан алгоритм обнаружения аналитического сигнала в форме пиков на основе анализа характерных точек второй и третьей производных. Модель апробировалась более чем на 3-х тысячах вольтамперограмм, где на одной кривой располагалось от 1 до 4 пиков. Регистрация вольтамперограмм проводилась по методике [8] на анализаторе ТА–07 (производства ООО «НПЦ Техноаналит», г. Томск). Ряд определяемых элементов и диапазон их концентраций:
- Cd – 0,0001 – 0,005 мг/дм3
- Zn – 0,0005 – 0,1 мг/дм3
- Pb – 0,0002 – 0,05 мг/дм3
- Cu – 0,0006 – 1,0 мг/дм3
Для минимизации высокочастотного шума при получении производных вольтамперограммы сглаживались методом скользящего среднего с окном в 12 мВ и число проходов = 100 [7] (параметры сглаживания характерны для методики [8] и определялись эмпирически).
Так как предложенный алгоритм обнаруживает точки перегиба, то без дополнительных расчётов можно использовать результаты алгоритма в построении каркасной модели пика [9], что увеличивает стабильность расчёта его высоты.
Рецензенты:
Гольдштейн А.Е., д.т.н., профессор, заведующий кафедрой информационно-измерительной техники Томский политехнический университет, г.Томск.
Сечин А.И., д.т.н., профессор, Федеральное агентство по образованию, НИУ РЭТ Томский политехнический университет, г. Томск.
Пачурин Г.В., д.т.н., профессор, зав. кафедрой «Производственная безопасность и экология» (ПБиЭ), Нижегородский государственный технический университет им. Р.Е. Алексеева, г.Нижний Новгород.
Библиографическая ссылка
Кузнецов В.В., Романенко С.В. ОБНАРУЖЕНИЕ АНАЛИТИЧЕСКИХ СИГНАЛОВ В ФОРМЕ ПИКОВ, НА ПРИМЕРЕ ОПРЕДЕЛЕНИЯ НЕКОТОРЫХ МЕТАЛЛОВ МЕТОДОМ ИНВЕРСИОННОЙ ВОЛЬТАМПЕРОМЕТРИИ // Современные проблемы науки и образования. 2014. № 3. ;URL: https://science-education.ru/ru/article/view?id=13760 (дата обращения: 11.02.2026).



