В процессе обучения студенты СПО испытывают определенные трудности при усвоении материала и, особенно, при применении изученного материала в профессиональной сфере. Одним из способов преодоления этих трудностей является достижение понимания обучающимися изучаемых понятий.
Основным средством достижения различных уровней понимания в обучении математики являются различные задания, отобранные педагогом. Однако просто использование заданий в обучении математике, как показывают наблюдения, далеко не всегда приводит к желаемому результату. С.А.Смирнов и В.В.Знаков в своих работах впервые выделили характеристики понимания: полноту, отчетливость и глубину. Необходимо сформулировать определенные требования к отбору заданий, обеспечивающих достижение характеристик понимания: полноты, отчетливости и глубины, которые в свою очередь, способствуют достижению соответствующих уровней понимания: понимание-узнавание, понимание-гипотеза, понимание-объединение.
Э.К.Брейтигам рекомендует при организации обучения, направленного на понимание старшеклассниками содержания курса алгебры и начала анализа, использовать следующие типы заданий:
-
задачи на актуализацию свойств «похожего» понятия для встраивания новых знаний в личный опыт обучающихся, на сравнение свойств нового и «похожего» понятия;
-
задачи различного уровня сложности для создания условий уровневой и профильной дифференциации усвоения в зависимости от: а) индивидуальных особенностей обучающихся; б) роли понятий в теме;
-
задачи, для решения которых необходимо использовать различные формы представления знаний, переход от одной формы представления информации к другой;
-
задачи на рефлексию своей и чужой учебно-познавательной деятельности;
-
задачи, раскрывающие смысловую сторону изучаемого явления, для активизаций мыслительной деятельности обучающихся через расширение смыслового пространства нового знания;
-
задачи, имеющие общую математическую модель, для одновременного предъявления обучающимся с последующим анализом всех задач, выбора общего и различий в предлагаемых задачах и предоставления возможности старшекласснику самому выбрать одну из задач для последующего решения.[1]
О.И. Плакатина предлагает отдавать предпочтение таким классам задач, особенности которых позволяют ярко выделить используемые приемы деятельности по достижению «понимающего» усвоения:
-
задачи, требующие перевода с одного языка на другой;
-
задачи с вариативными условиями;
-
задачи с «парадоксальными» данными или результатами;
-
«провокационные» задачи;
-
задачи с недостающими или избыточными данными. [5]
Е.Н.Дронова выделяет следующие основные типы учебно-познавательных задач, направленных на понимающее усвоение математики:
- задачи на актуализацию субъектного опыта учащихся;
- задачи на постижение смысловой стороны учебного материала;
- задачи на использование разных знаково-символических средств;
- задачи на выяснение структурных связей;
- задачи на применение изучаемого понятия;
- задачи на рефлексию;
- задачи - творческие задания. [4]
Т.В.Гринева предложила для повышения качества понимания обучающимися учебного материала школьного курса алгебры и начал анализа следующие принципы отбора содержания заданий:
- принцип многоаспектности;
- принцип последовательности;
- принцип единства содержания и способов кодирования представленной информации;
- принцип единства содержательной и процессуальной стороны обучения;
- принцип сравнения. [3]
В своём исследовании Т.В.Гринева выделила уровни и определила критерии для каждого уровня. Поскольку мы считаем эти критерии уровней характеристик понимания приемлемыми для нашего исследования, то мы подбирали задания, опираясь на данные критерии. Решение заданий, отобранных с использованием даны критериев, позволит обучающимся перейти с одного уровня, для каждой характеристики понимания, на другой.
При составлении принципов отбора заданий мы руководствовались тем, что, отобранные задания, должны позволить в полной мере сформировать у обучающихся все характеристики понимания: полноту, отчетливость и глубину. Сформированность характеристик понимания дает возможность достичь различных уровней понимания и выйти на самый высокий уровень понимания - понимание-объединение.
В основном, соглашаясь с принципами отбора заданий предложенными Т.В. Гриневой, мы изменили их с учётом особенностей студентов СПО и содержания учебного материала системы СПО.
В разрабатываемую нами систему принципов отбора заданий мы включили принцип последовательности, выделенный Т.В.Гриневой. Данный принцип необходим, так как задания должны следовать от более простого к более сложному, они должны способствовать установлению взаимосвязей между понятиями темы, выстраиванию иерархии понятий. Без соблюдения данного принципа невозможно достичь ни одной характеристики понимания.
Включили принцип многоаспектности, выделенный Т.В.Гриневой. Этот принцип позволяет, в частности, включить при его реализации типы учебно-познавательных задач, выделенные Е.Н. Дроновой и направленные на применение изучаемого понятия. Применение принципа многоаспектности позволит формировать у обучающихся такую характеристику понимания, как полнота.
Чтобы формировать следующую характеристику понимания - отчетливость, необходимо использовать задачи, в которых придется полученные знания представлять в различных формах. Для студентов СПО, в силу слабых теоретических знаний, важно использовать различные формы представления изучаемого материала, особенно, для абстрактных научных понятий. Также важно соединять теоретический материал в процессе обучения с жизненным опытом студентов. Это привело к необходимости использования при отборе задач принципа единства содержания и способов кодирования представленной информации, выделенного Т.В.Гриневой. Данный принцип содержит в себе выделенный принцип отбора заданий, для решения которых необходимо использовать различные формы представления знаний, переход от одной формы представления информации к другой (Э.К.Брейтигам), принцип отбора задач, требующих перевода с одного языка на другой (О.И.Плакатина) и принцип отбора задач на использование разных знаково-символических средств (Е.Н.Дронова). Но применение только принципа единства содержания и способов кодирования представленной информации, не позволит сформировать данную характеристику на высоком уровне.
Проблемы выделения учащимися взаимосвязей свойств понятий внутри темы, а также, анализ ошибок студентов и собственный опыт, привел к необходимости выделения дополнительных принципов.
Для формирования отчетливости понимания на более высоком уровне у обучающихся, необходимо включить задания, в которых нужно рассматривать сравнения схожих понятий, а также задания, где рассматриваются различные формулировки определения того или иного понятия. Все это привело к необходимости введения такого принципа, как принцип сопоставления. Данный принцип содержит в себе, выделенный принцип отбора заданий на актуализацию свойств «похожего» понятия для встраивания новых знаний в личный опыт обучающихся, на сравнение свойств нового и «похожего» понятия (Э.К.Брейтигам), «провокационные» задачи, задачи с вариативными условиями (О.И.Плакатина). Выполнение заданий, направленных на реализацию принципа сопоставления, позволит обучающимся достичь более высокого уровня отчетливости понимания. Задания, удовлетворяющие перечисленным выше принципам, направлены также на формирование такой характеристики понимания как глубина.
Для осуществления возможности достижения более высоких уровней формирования таких характеристик понимания как глубина и полнота, мы пришли к необходимости выделения принципа объединения. Данный принцип содержит в себе, выделенный Э.К. Брейтигам, принцип отбора заданий, раскрывающих смысловую сторону изучаемого явления, для активизации мыслительной деятельности обучающихся через расширение смыслового пространства нового знания, а также, принцип отбора задач на выяснение структурных связей (Е.Н.Дронова).
Рассмотрим более подробно содержание каждого из принципов, которые применялись нами для отбора заданий, направленных на формирование характеристик понимания.
1. Принцип последовательности заключается в соблюдении порядка представления заданий, направленных на достижение различных характеристик понимания. В процессе решения заданий, обучающиеся должны сначала усвоить различные интерпретации понятия, затем на их основе усвоить основные способы действия и знаково-символического кодирования изучаемого материла, определить его степень значимости.
Данный принцип отбора заданий отвечает общим принципам дидактики и направлен на реализацию принципа систематичности и последовательности, а также принципа доступности, выделенные М.Н.Скаткиным. Соблюдение данного принципа при отборе заданий является необходимым условием усвоения учебного материала, а, следовательно, и достижения понимания этого материала. Поэтому мы выделили в своей работе принцип последовательности первым.
В соответствии с данным принципом, сначала необходимо рассмотреть задачи на усвоение определения понятия, общего смысла понятия производной, а затем задачи, где производная используется для выяснения поведения функции в той или иной точке и т.д.
2. Принцип многоаспектности заключается в отборе заданий, решение которых позволяет рассмотреть изучаемое понятие в различных сферах применения, Выделить геометрический и физический смыл понятий. Задания, нацеленные на достижение понимания, должны быть направлены на геометрическую и физическую интерпретацию понятия, лингвистический анализ лексемы понятия, установление взаимосвязей и отношений изучаемых понятий с ранее изученным материалом.
Формулировка данного принципа нами была несколько изменена, так как Т.В.Гринева в своей работе основное внимание уделяла постижению различных аспектов смысла математических понятий, мы же используем данный принцип для формирования основных характеристик понимания в процессе усвоения содержания учебного материала.
В соответствии с данным принципом, мы отбирали задания, которые охватывают различные применения изучаемого материала (на примере изучения темы «Дифференциальное исчисление» курса математики). Подобраны задания на нахождение геометрического и физического смысла производной, вычисление производной с помощью таблицы производных и основных правил дифференцирования, задания на вычисление приближенного значения с помощью дифференциала, а также задачи оптимизации. Реализация этого принципа способствует формированию целостности знания.
3. Принцип единства содержания и способов кодирования представленной информации заключается в необходимости применения в учебном процессе различных форм представления формируемого понятия. Задания должны охватывать графическую, знаково-символическую, вербальную, схематическую формы представления понятия, переход от одной формы представления к другой. При решении заданий отобранных по данному принципу можно использовать специально разработанное программное обеспечение, которое на данном этапе развития информационных технологий не создает психологического барьера у обучающихся, а позволит более быстро перейти от одной формы представления изучаемого понятия к другой [2].
Приведем примеры некоторых заданий, отобранных в соответствии с данным принципом, которые необходимо рассмотреть при изучении темы «Дифференциальное исчисление».
Пример 1: На рисунке 1 изображен график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
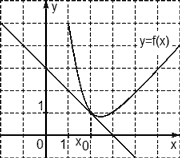
Рис.1. График функции и касательной к графику
Задания данного типа необходимо рассмотреть, так как часто обучающиеся, зная геометрический смысл производной, не могут перенести полученные знания на задания, представленные в графическом виде. Здесь необходимо рассмотреть задания, где понадобится вычислить тангенс, как острого угла, так и тупого, а также рассмотреть задачи, где абсцисса точки касания х0 расположена во второй четверти.
Приведем еще один пример задания, отобранного по данному принципу.
Пример 2: По графику функции f(x), изображенному на рисунке 2, определить:
а) промежутки, где ![]() ;
;
б) промежутки, где ![]() ;
;
в) точки, где ![]() ;
;
г) точки, где ![]() не существует.
не существует.
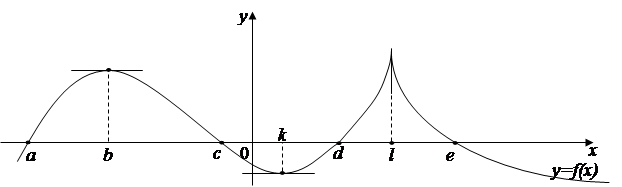
Рис.2. График функции
При решении данной задачи от обучающихся потребуется вспомнить свойства функции и производной функции, установить взаимосвязь между данными свойствами, а также, представить данные в различных формах: знаково-символической и вербальной. Если обучающиеся справляются с данной задачей, то это говорит об отчетливости понимания производной функции.
Использование специальных заданий, которые позволяют сначала обучающимся на наглядном уровне усвоить изучаемое понятие, дают возможность им перейти к осознанному применению алгоритма нахождения производной представленной в различных формах. Следовательно, данный принцип позволяет сформировать такую характеристику понимания как отчетливость.
4. Принцип сопоставления заключается в необходимости включения заданий, направленных на выявления умения обучающимися оперировать полученными знаниями при решении заданий нового содержания в различных ситуациях. Также задания, отобранные по данному принципу, должны содержать задания на сравнения схожих понятий.
Данный принцип включает в себя принцип единства содержательной и процессуальной стороны обучения, выделенный Т.В.Гриневой, но дополнен заданиями на сравнения схожих понятий, что является существенным для формирования отчетливости понимания на высоком уровне.
Приведем некоторые примеры.
Пример 3: Найдите угловой коэффициент касательной, проведенной к параболе в данной на ней точке.
Практика показывает, что зная геометрический смысл производной, при изменении формулировки задания, у обучающихся возникают трудности при решении.
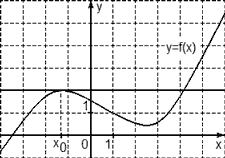
Рис. 3. График функции
Пример 4: На рисунке 3 изображен график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Здесь представлен частный случай, когда тангенс угла наклона касательной равен нулю.
В рассматриваемых выше примерах, даются задания с другой формулировкой, непривычной для обучающихся. В связи с этим, данные задания воспринимаются обучающимися по-другому и вызывают трудности при решении.
Также, в соответствии с данным принципом, необходимо рассмотреть задания на сравнения схожих понятий. Например, найти максимальное значение функции, точки максимума, наибольшее значение функции и т.д.
Задания, которые были отобраны в соответствии с принципом сопоставления, направлены на отработку отчетливости и глубины понимания.
5. Принцип объединения состоит в том, что задания должны содержать задачи, для решения которых от обучающихся требуется выявление сущностных связей различных понятий, а также умение одновременного использования как раннее полученных знаний, так и вновь изученных понятий. При этом, включаются задания, где от обучающихся требуется объяснения «своими словами» тех или иных аспектов понятия, исходя из ранее полученных знаний.
Приведем некоторые примеры заданий, отвечающих данному принципу.
Пример 5: Проведите исследование функции ![]() и постройте её график.
и постройте её график.
В этом примере, при проведении исследования функции, обучающимся необходимо выявить взаимосвязь между свойствами функции и производной функции, используя выявленные взаимосвязи и объединив свойства понятия с их геометрическим представлением, построить график функции.
Пример 6: Постройте эскиз графика функции ![]() , обладающей следующими свойствами:
, обладающей следующими свойствами:
![]() ,
, ![]() ,
, ![]() - не существует,
- не существует, ![]() ,
, ![]() .
.
В данном примере, обучающимся также необходимо выявить взаимосвязь между свойствами функции и производной функции, используя данные взаимосвязи и, объединив свойства понятия с их геометрическим представлением, построить график функции. Но, в отличие от предыдущего примера, где дается алгоритм исследования функции, обучающимся приходится самостоятельно без алгоритма, объясняя то или иное свое действие, применять раннее полученные знания.
Пример 7: На рисунке 4 изображен график производной функции f(x), определенной на отрезке [−10; 4]. Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.
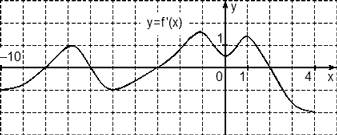
Рис.4. График производной функции
Данные задания вызывают у обучающихся трудности при решении, так как, кроме умений, используемых в предыдущих двух примерах, от обучающихся требуется объяснения своими словами тех или иных аспектов, исходя из ранее полученных знаний.
Задания, которые были отобраны в соответствии с принципом объединения, дают более полное представление изучаемых понятий и направлены в основном на достижение глубины и полноты понимания.
Реализация всех перечисленных ранее принципов при подборе заданий позволяют целенаправленно формировать у обучающихся все характеристики понимания.
Необходимо четко понимать, что решение заданий, отобранных лишь только по одному принципу, не дает возможность сформировать у обучающихся на высоком уровне ни одной характеристики понимания. Каждый принцип отбора заданий позволяет формировать различные характеристики понимания на различных уровнях. Например, принцип многоаспектности в большей мере направлен на формирование полноты понимания, но также решение заданий, отобранных в соответствии с данным принципом, позволяет формировать у обучающихся отчетливость и глубину понимания. Реализации принципа объединения дает возможность обучающимся достичь высокого уровня глубины, полноты и отчетливости понимания. Формирование у обучающихся всех характеристик понимания на высоком уровне возможно лишь при совместной реализации всех принципов отбора заданий.
Реализация всех принципов отбора заданий позволит обучающимся перейти от уровня понимания - понимание-узнавание к уровню понимание-гипотеза, а затем и к самому высокому уровню понимания – понимание-объединение.
Рецензенты:
Брейтигам Э.К., д.п.н., профессор, профессор Алтайской государственной педагогической академии, г.Барнаул.
Веряев А.А., д.п.н., профессор, профессор Алтайской государственной педагогической академии, г.Барнаул.
Библиографическая ссылка
Щербинина С.Г. ПРИНЦИПЫ ОТБОРА ЗАДАЧ ДЛЯ ОБЕСПЕЧЕНИЯ ПОНИМАНИЯ СТУДЕНТАМИ УЧЕБНОГО МАТЕРИАЛА // Современные проблемы науки и образования. 2014. № 3. ;URL: https://science-education.ru/ru/article/view?id=13675 (дата обращения: 11.02.2026).



