Введение
К настоящему времени ни у кого не вызывает сомнений практическое значение и необходимость использования человеком большого класса оптических систем. К ним можно отнести телескопы, оптические локационно-измерительные системы, технологические установки с использованием мощных лазерных пучков [7; 16].
Принцип действия адаптивных оптических систем (АОС) в самом общем случае можно охарактеризовать как прямое или косвенное измерение пространственного распределения амплитуды и фазы поля на апертуре оптической системы и построение оптимального по заданному критерию алгоритма, который в этом случае позволяет в значительной степени компенсировать вредное влияние турбулентности, обеспечивая функционирование оптических систем с заданным критерием качества. Особенно следует отметить тот факт, что в теоретических и экспериментальных исследованиях российских и зарубежных ученых показано, что адаптивное управление фазой оптического излучения - в большинстве случаев единственный способ компенсировать вредное влияние турбулентности. В настоящем обзоре изложены основные результаты, полученные авторами в последние годы. При этом направленность исследований определяли конкретные инженерные задачи, стоящие перед авторами. Поэтому сразу необходимо оговорить тот факт, что авторы не претендуют на полное и всестороннее рассмотрение проблемы создания адаптивных оптических систем.
Отметим следующие основные направления исследований, проводимых авторами:
-
повышение быстродействия алгоритмов апертурного зондирования и фазового сопряжения;
-
методы восстановления фазового фронта по результатам измерений интенсивности Фурье-образа светового поля;
-
кумулянтные методы оценки потенциальных характеристик адаптивных оптических систем;
-
разработка новых конструктивных решений при создании элементной базы адаптивной оптики;
-
разработка новых структур адаптивных оптических систем на базе синтезированных алгоритмов [9; 15; 41].
1. Повышение быстродействия алгоритмов апертурного зондирования и фазового сопряжения
При практической реализации метода апертурного зондирования апертура оптической системы делится обычно на N субапертур, каждая из которых осуществляет пространственную модуляцию фазы падающей на нее волны. Пробные воздействия, как правило, задаются одновременно на всех апертурах и отличаются частотами модуляции [3; 12]. Большинство известных систем с многоканальной фазовой модуляцией используют те или иные способы выделения управляющих сигналов, пропорциональных градиенту интенсивности на точечном фотодетекторе. Такие алгоритмы в теории оптимизации относят к алгоритмам первого порядка.
Для дальнейшего анализа алгоритмов необходимо разграничение по типу адаптивного зеркала, используемого в АОС. В случае использования сегментированного корректора фазового фронта повышение быстродействия может обеспечить алгоритм второго порядка [3], учитываемый в управлении
(1)
где 
- вектор-столбец управляющих сигналов на i-м шаге; С' - матрица коэффициентов:
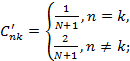
- вектор-градиент интенсивности (сигналы с выхода полосовых фильтров АОС).
В случае использования в АОС гибких зеркал, например мембранного типа, наряду с проблемой слабой сходимости алгоритмов апертурного зондирования существует проблема [3], связанная с тем, что приложение управляющего напряжения к одному приводу гибкого адаптивной зеркала вызывает его деформацию в точках крепления других приводов. Основная причина такой ситуации состоит в том, что гибкая мембрана является распределенной системой. Для решения этой проблемы, наряду с использованием алгоритма второго порядка [3], необходимо учитывать геометрию адаптивного зеркала. В этом случае обычно вводится понятие матрицы податливости адаптивного зеркала 
с элементами 
. Физический смысл этой матрицы состоит в том, что она описывает отклик гибкого зеркала при подаче управляющего напряжения на i-й привод. При этом элементы матрицы равны деформации зеркала в i -й точке. Очевидно, что если экспериментально или теоретически получить такую матрицу для конкретного адаптивного зеркала, затем вычислить обратную ей 
, то, домножив вектор управляющих сигналов вида (1) на , можно получить алгоритм второго порядка, который учитывает геометрию зеркала и сохраняет все свои преимущества. Вероятно, что особую привлекательность такой алгоритм, подробно описанный в [12], имеет при использовании в качестве адаптивных зеркал сочетания пьезоэлектрических пластин различной формы. Однако игнорирование геометрии мембранных и гибких пьезоэлектрических зеркал в этом случае может повлечь за собой полную неработоспособность АОС.
Исследования алгоритмов апертурного зондирования второго порядка с точки зрения их быстродействия, проведенные в [3; 12], показали, что эти алгоритмы позволяют значительно, в некоторых случаях в десятки раз, повысить быстродействие АОС. Особо следует отметить тот факт, что использование управления в преобразованных координатах (и матрицы ) может обеспечить устойчивость процесса поиска глобального экстремума.
Наряду с методами апертурного зондирования известен метод фазового сопряжения, предусматривающий непосредственное измерение распределения фазы на апертуре оптической системы, вычисление вектора управляющих сигналов и коррекцию по заданному критерию фазового фронта с помощью адаптивного зеркала. При реализации метода фазового сопряжения также существует ряд проблем, которые приходится решать ученым и разработчикам систем: во-первых, это невозможность прямого измерения фазового распределения; во-вторых, необходимость преобразования массива значений фазы в точках апертуры оптической системы в вектор управляющих сигналов адаптивного зеркала. Это связано с тем, что размерность и базис вычисленного распределения фазы не совпадают с размерностью и базисом адаптивного зеркала.
К тому же, как и в предыдущем случае, при синтезе алгоритмов фазового сопряжения необходимо учитывать вид адаптивного зеркала, используемого в АОС. Классификация алгоритмов косвенного измерения параметров фазового фронта представлена на рис. 1.
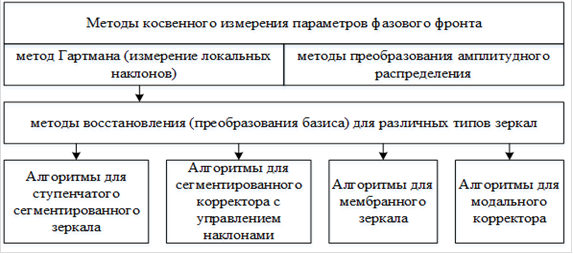
Рис. 1. Классификация алгоритмов фазового сопряжения.
Рассмотрим подробнее математические методы, используемые при восстановлении фазового фронта по результатам измерения его локальных наклонов. В АОС с сегментированным корректором фазового фронта с управлением сдвигами [2] или с управлением сдвигами и наклонами [29] целесообразно использовать алгоритм кусочно-линейной аппроксимации, описанный в [24]. В АОС с гибким мембранным зеркалом лучшие результаты дает применение алгоритма восстановления фазового фронта на основе математического аппарата нормализованных В-сплайнов [8; 32]. При использовании в качестве корректора фазового фронта модального корректора целесообразно применение алгоритма [1], позволяющего непосредственно получать вектор коэффициентов при полиномах Цернике из массива измерений локальных наклонов фазового фронта. Алгоритмы из [1; 16; 24; 30] по сравнению с известными позволяют существенно сократить объем вычислительных затрат при требуемой точности восстановления фазового фронта и могут быть легко реализованы на базе вычислительных средств.
2. Кумулянтные методы оценки потенциальных характеристик адаптивных оптических систем
При создании адаптивных оптических систем возникает вопрос анализа их точностных характеристик. Это связано с тем, что по своей структуре адаптивные системы являются достаточно сложными. Для анализа точностных характеристик их можно условно разбить на три подсистемы:
-
подсистема регистрации оптического излучения с искаженной фазой;
-
подсистема восстановления фазового фронта по результатам измерений и вычисления вектора управляющих сигналов (для систем апертурного зондирования - подсистема формирования зондирующих сигналов и вектора управляющих воздействий);
-
подсистема коррекции фазового распределения (как правило, гибкое адаптивное зеркало).
Подсистема регистрации оптического излучения адаптивных оптических систем в общем случае представляет собой один фотоприемник или матрицу фотоприемников. Анализ потенциальных характеристик фотоприемника в случае приема пуассоновских сигналов на фоне пуассоновских шумов не составляет большого труда. Несколько сложнее обстоит дело при анализе статистических свойств пуассоновских шумов квадрантных фотоприемников, являющихся неотъемлемой частью датчика гартмановского типа. Для этого случая авторами в [31] предложен оригинальный подход, основанный на анализе суммы и разности кумулянтов искомых случайных пуассоновских процессов. На базе полученных выражений для плотности распределения синтезирована структура оптимального оценивания с учетом суммарно-разностной обработки пуассоновских сигналов.
Анализ точностных характеристик различных алгоритмов восстановления фазового фронта проведен в [4; 14]. При этом была найдена зависимость вида:
, (2)
где 
- дисперсии ошибки восстановления фазового фронта; 
- дисперсии измерений; 
- коэффициент, зависящий, как правило, от числа каналов управления АОС 
и других параметров алгоритма 
.
Анализ точностных характеристик адаптивных оптических систем апертурного зондирования в [6; 11; 50] осуществлен на базе кумулянтного описания шумов в каналах управления. Коротко суть метода состоит в следующем. Вводится понятие отрицательного приращения функционала качества за счет шумов в каналах управления АОС 
в виде
, (3)
где 
- максимально достижимое значение функционала качества; 
- максимальное значение функционала качества при наличии шумов в каналах управления.
Угловыми скобками здесь и в дальнейшем будем обозначать символ математического ожидания. Наряду с математическим ожиданием вводится его дисперсия 
. Очевидно, что, оперируя с этими величинами, возможно достаточно эффективно оценить качество различных алгоритмов. Предложенный метод позволяет найти значения и в случае наличия в каналах управления шумов различной природы - гауссовских, пуассоновских и других. Необходимо только подставить в общее выражение соотношения для соответствующих кумулянтов, преобразовать его и с помощью ЭВМ провести соответствующий анализ [8; 17].
При анализе подсистемы коррекции фазового фронта наряду с задачей анализа качества аппроксимации фазового фронта конкретным адаптивным зеркалом возникает вопрос оптимизации числа пространственных мод такого зеркала. Суть данной научной задачи состоит в следующем. Датчик фазового фронта производит измерение локальных наклонов фазового фронта в 
точках. Адаптивное зеркало имеет 
степеней свободы, 
. Очевидно, что при увеличении будет увеличиваться в соответствии с выражением (2), а при увеличении будет уменьшаться ошибка аппроксимации фазового фронта. Таким образом, имеем классическую задачу оптимизации при заданном значении. Задача оптимизации для адаптивного зеркала произвольного вида решена в [10]. Для описания поверхности зеркала использован аппарат нормализованных параболических сплайнов. Выбор именно этого математического аппарата обусловлен тем, что первоначально он был разработан для описания деформаций мембран. Анализ точности описания деформаций показал, что повышение степени сплайна в принципе нецелесообразно, так как вычислительные затраты возрастают при незначительном росте точности.
Разработанный метод [1] выбора числа пространственных мод с учетом шумов датчика гартмановского типа позволяет ограничить число степеней свободы произвольного корректора фазового фронта, исходя из конкретных условий функционирования адаптивной оптической системы. Проведенный анализ показал, что для уменьшения дисперсии ошибки, вызванной шумами измерений, в общем случае необходимо увеличивать число квадрантных фотоприемников датчика гартмановского типа.
При использовании метода сплайн-аппроксимации появляется возможность с достаточной степенью точности численно-аналитическим методом найти элементы матрицы нормальной системы уравнений в виде линейной комбинации коэффициентов нормализованного -сплайна. При этом в качестве априорной информации для построения сплайна, описывающего адаптивное зеркало, можно использовать как собственно значения функций отклика, так и значения их частных производных. Следует особо отметить, что наряду с адаптивными зеркалами на базе пьезопластины предложенным методом могут быть оптимизированы и адаптивные оптические системы с мембранными зеркалами, управляемые различными видами актюаторов.
3. Новые конструктивные решения при создании элементной базы адаптивной оптики
Разработка новой элементной базы является важным звеном в создании адаптивных оптических систем. Наиболее простым по конструкции является сегментированный корректор фазового фронта [2]. Он содержит 23 привода размером 20x20 мм. Крайние угловые приводы апертуры 5x5 элементов исключены, чтобы форма апертуры корректора приближалась к круглой. Дополнительно введены 3 привода, позволяющие управлять положением апертуры.
Более перспективным направлением в задаче создания фазовых корректоров оказалось использование круглых пьезоэлектрических пластин [22; 23; 26]. Зеркало состоит из металлической подложки, прикрепленной к пьезоэлектрической пластине. Обратная сторона пьезоэлектрической пластины оптически отполирована, и на нее напылены управляющие электроды из хорошо отражающего материала, например серебра или алюминия. Существенным отличием разработанной конструкции явилось отсутствие дополнительной стеклянной отражающей пластины. Ввиду этого на экспериментальном образце [22] удалось получить значительные (до 50 мкм) деформации при диаметре 50 мм. Диапазон частот при такой величине деформаций составлял до 1 кГц.
В работе [29] представлены варианты конструкции адаптивного зеркала. Особенностью управления таким зеркалом является то, что в качестве управляющих сигналов могут быть использованы непосредственно сигналы с выхода датчика Гартмана. В качестве активных элементов в устройстве использованы пьезоэлектрические диски, конструкция которых была описана выше [10].
Следующая конструкция [25] может быть использована при создании адаптивных зеркал крупных телескопов. Ее особенность состоит в том, что в качестве активных элементов использованы пластины типа [22] шестиугольной формы. Пьезопластины прикреплены к массивному основанию по образующей. Благодаря тому что в качестве активного элемента использована не одна пьезопластина, а несколько, снимается конструктивное ограничение на размер зеркала (диаметр апертуры). Для вычисления вектора управляющих сигналов такого зеркала целесообразно использовать аппарат нормализованных 
-сплайнов.
Наряду с устройствами коррекции фазового распределения отражательного типа в настоящее время разрабатываются различные корректоры, работающие на пропускание. К таким корректорам можно отнести предложенные в [21] электрооптические кристаллы LiNb03. Фазовый корректор представляет собой набор электрооптических кристаллов размером 30x20x2. На обе стороны кристаллов нанесены управляющие электроды, форма которых соответствует требуемой моде фазовой коррекции (наклон, дефокусировка и т.д.). Перед коррекцией оптический пучок сжимается с помощью цилиндрической линзы. На выходе из кристалла с помощью аналогичной линзы форма пучка преобразуется в первоначальную. Соединяя последовательно требуемое число кристаллов, можно обеспечить заданный диапазон и модовый состав фазовой коррекции.
При разработке практически всех исполнительных устройств адаптивных оптических систем - пьезоэлектрических элементов, электрооптических кристаллов, ячеек Керра - для управления ими требуется высокое напряжение (сотни и тысячи вольт с частотой до 5 кГц). Таким образом, перед разработчиками систем встала задача создания специализированных усилителей, способных работать на емкостную нагрузку и обеспечивающих высокое, порядка нескольких тысяч вольт, выходное напряжение.
Авторами была разработана [27; 36; 49] конструкция такого усилителя. Особенность работы данного усилителя заключается в том, что при увеличении входного напряжения цепочка «операционный усилитель - парафазный каскад - блокинг-генераторы» обеспечивает формирование специальной последовательности импульсов для управления транзисторами выходного каскада, работающими в ключевом режиме.
Особенностью схемы усилителя является то, что в зависимости от формы входного сигнала (скорости его изменения) изменяется частота управляющих импульсов, а в случае если этого недостаточно для формирования на емкости нагрузки соответствующего управляющего сигнала, то и длительность импульсов. Такая совокупность технических решений позволила обеспечить высокую линейность данного усилителя. Ввиду того что выходные транзисторы работают в ключевом режиме, выходная мощность, рассеиваемая на них, сравнительно мала.
4. Разработка новых структур адаптивных оптических систем на базе синтезированных алгоритмов
Конечной целью научного творчества является реализация полученных теоретических результатов в виде структур новых систем. В [33; 39] приведены структурные схемы, позволяющие реализовать па практике алгоритм кусочно-линейной аппроксимации фазового фронта вида [6].
На рис. 2 приведена структурная схема датчика фазового фронта [5], реализующего алгоритм вида (1) [3]. Сегментированный корректор фазового фронта модулирует каждый элементарный участок волнового фронта частотой 
. Фотоприемник регистрирует отраженный от корректора сигнал. С помощью системы полосовых фильтров выделяется сигнал, пропорциональный градиенту интенсивности на точечном фотодетекторе. С помощью блоков 8, 9, 10 происходит весовая обработка и формирование вектора выходных сигналов, элементы которого пропорциональны значениям фазы в соответствующих точках апертуры.
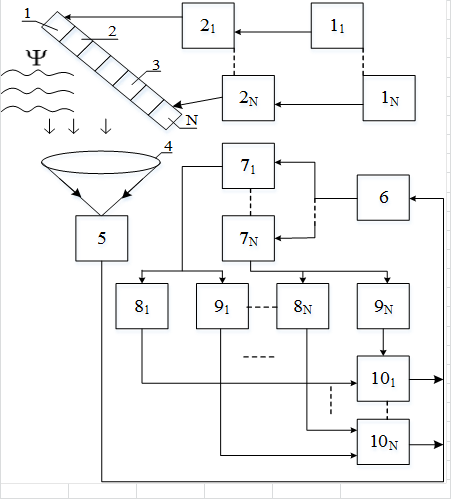
Рис.2. Структурная схема датчика фазового фронта.
Разработанный датчик может служить основой для системы апертурного зондирования, использующей два адаптивных зеркала: первое с широкой частотной характеристикой и малым динамическим диапазоном - для модуляции оптического излучения и измерения распределения фазы на апертуре, и второе, обладающее более узкой частотной характеристикой, зато широким динамическим диапазоном, - собственно для коррекции искаженного фазового фронта [20; 46; 47].
На рис. 3 приведена структура адаптивной оптической системы с гибким адаптивным зеркалом [40]. Принцип работы данной системы основан на алгоритме, описанном в [12]. Фактически в систему апертурного зондирования с многоканальной фазовой модуляцией дополнительно введено т2 весовых элементов 10 и соответствующие связи. Таким образом, в данной системе реализуется градиентный алгоритм второго порядка с учетом свойств гибкого адаптивного зеркала.
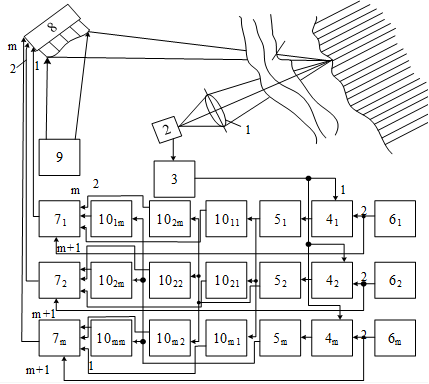
Рис. 3. Адаптивная оптическая система апертурного зондирования: 1 – линза; 2 - точечный фотодетектор; 3 - предварительный усилитель; 4 - синхронные детекторы; 5 - усилители; 6 - генераторы пробных сигналов; 7 - сумматоры; 8 — мембранное адаптивное зеркало; 9 - лазер; 10 - весовые элементы; ψ — турбулентная атмосфера.
В работе [37] предложен датчик фазового фронта интерференционного типа. Принцип действия такого датчика состоит в следующем. Оптический квантовый генератор и расширитель пучка формируют опорный пучок, в который с помощью фазового транспаранта вносятся фазовые сдвиги. Величина фазового сдвига в зависимости от номера канала устройства равна 
, 
, где - длина волны излучения оптического квантового генератора. Измеряемый фазовый фронт попадает на оптические делители, коэффициент деления которых равен 
, . Очевидно, что при таком соотношении коэффициентов деления интенсивность измеряемого пучка поделится поровну между всеми 
каналами.
Рассмотрим принцип действия тангенциального датчика фазового фронта. Для аппроксимации функций отклика гибкого адаптивного зеркала [33] используем систему полиномов Цернике, ортогональных (ортонормированных) внутри единичной окружности или окружности радиусом R, представленных в полярных координатах r, θ:
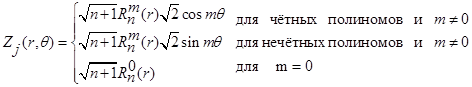(4)
где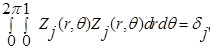 
.
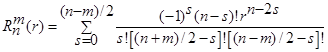В используемом методе подлежат измерению тангенциальные локальные наклоны, пропорциональные величинам вида: 
, 
. Для измерения этих величин предлагается использовать двухплощадные фотоприемники, расположенные в точках апертуры на концентрических окружностях (рис. 4) [18; 19; 42-45; 48].
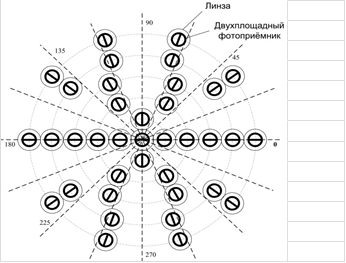
Рис. 4. Расположение двухплощадных фотоприемников в точках апертуры и линз на концентрических окружностях.
На рисунке 5 представлена функциональная схема разработанного датчика фазового фронта, содержащего: N линз 1, матрицу из N двухплощадных фотоприемников 2, N дифференциальных усилителей 3, 16N масштабных усилителей блока суммирования 4, 16 сумматоров блока суммирования 5, группу из 40 масштабных усилителей 6, вторую группу из 15 сумматоров 7 [18].
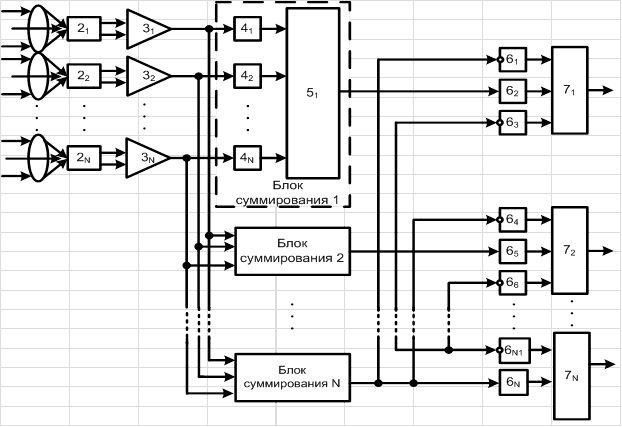
Рис. 5. Функциональная схема датчика тангенциального типа.
Искаженный волновой фронт фокусируется матрицей линз 1 на матрицу двухплощадных фотоприемников 2. При этом в каждом локальном участке, ограниченном апертурой линзы, сфокусированное пятно смещается относительно оптической оси в зависимости от локального наклона фазового фронта 
в точках с координатами 
, 
.
Наличие искажений фазового фронта приводит к появлению разностных сигналов на выходе фотоприемников 2, которые усиливаются дифференциальными усилителями 3, выходные сигналы которых будут пропорциональны величинам 
, при этом они будут являться по существу тангенциальными производными. Затем сигналы с выхода дифференциальных усилителей 3 поступают на блоки суммирования, где вычисляются сигналы, пропорциональные элементам вектор-столбца правой части:
, 
.
При этом коэффициенты усиления Ky масштабных усилителей 4 блока суммирования вычисляются в соответствии с выражением 
.
Выходные сигналы блоков суммирования 5, пропорциональные величине Cj, поступают на входы группы масштабных усилителей, коэффициенты усиления которых вычисляются 
, 
.
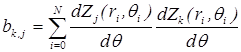При этом учитываются только ненулевые элементы. Выходные сигналы вторых масштабных усилителей 6 поступают на входы первого, второго, третьего, четвертого, пятого, шестого, седьмого, восьмого, десятого, одиннадцатого, двенадцатого, тринадцатого, четырнадцатого, пятнадцатого, шестнадцатого сумматоров второй группы сумматоров 7, с выхода которых снимаются сигналы aj, пропорциональные коэффициентам разложения в базисе Цернике.
При этом сигналы с выхода датчика могут быть использованы непосредственно для подачи на вход гибкого пьезоэлектрического зеркала адаптивной оптической системы, что существенно упрощает ее конструкцию.
Заключение
Узкие рамки статьи не позволили подробно осветить все полученные авторами результаты. Поэтому основной акцент в обзоре был сделан на те из них, которые в представленном виде не публиковались. Однако авторы надеются, что эти результаты все же заинтересуют специалистов, работающих в области теории и практики адаптивной оптики.
Необходимо отметить, что в целом исследования в области адаптивной оптики на данном этапе не только привели к созданию приборов и систем, способных решать свои прямые задачи, но и существенно расширили рамки этой области. Разработанная теория и приборы, в частности устройства измерения и восстановления волнового фронта, могут эффективно использоваться при проведении фундаментальных исследований атмосферы. Например, при изучении процессов развития вихревых образований, которые по своей природе имеют характер фазовых объектов и в естественных условиях не могут быть визуализированы.
Рецензенты:
Звездина М.Ю., д.ф.-м.н., доцент, зав. кафедрой «Радиоэлектроника», Минобрнауки России, Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Донской государственный технический университет», г.Ростов-на-Дону.
Габриэльян Д.Д., д.т.н., профессор, заместитель начальника научно-технического комплекса «Антенные системы» по науке, Федеральный научно-производственный центр ФГУП «РНИИРС», г. Ростов-на-Дону.
Библиографическая ссылка
Безуглов Д.А., Решетникова И.В., Сахаров И.А. АДАПТИВНЫЕ ОПТИЧЕСКИЕ СИСТЕМЫ: МЕТОДЫ И УСТРОЙСТВА ВОССТАНОВЛЕНИЯ И КОРРЕКЦИИ ФАЗОВОГО ФРОНТА // Современные проблемы науки и образования. – 2014. – № 4. ;URL: https://science-education.ru/ru/article/view?id=13670 (дата обращения: 19.04.2024).