Введение
В настоящее время актуальной задачей является взаимодействие спутниковых и наземных навигационных систем, к которым предъявляется ряд механических и радиолокационных требований. Учитывая расстояния между источником и приемником сигнала, решающую роль играет угол направления локатора, который зависит не только от точности угла задания, но и возможного его отклонения в результате ветровых воздействий [2, 5]. В данной работе определяются параметры электропривода поворотного механизма антенны, а именно вращающий момент электропривода и моменты сопротивления, оказываемые ветровыми нагрузками.
Целью работы является моделирование физического процесса обтекания воздушным потоком рефлектора антенны и определение его геометрических размеров и граничных условий.
Для решения данной задачи применяется численное моделирование вязкого обтекания с различными углами атакирефлектора антенны, выполненного в форме гиперболоида [1].
Упрощенный 3D-чертеж геометрии рефлектора антенны изображен на рис. 1.
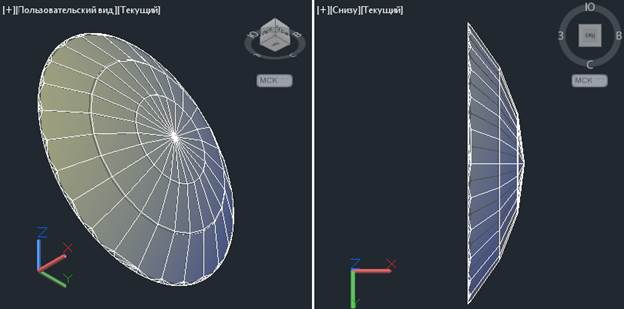
Рисунок 1 – Упрощенный 3D-чертеж геометрии рефлектора антенны
Зеркало антенны имеет диаметр 4.5 м, скорость ветра 35 м/с, угол атаки ветра варьируется от 22,50 до 157,50 с шагом 22,5 градусов, число Рейнольдса приблизительно равно Re=8×106.
Задание условий моделирования
В используемом программном пакете применяется метод конечных элементов для решения численных уравнений, поэтому в качестве объемной расчетной плоскости выбран параллелепипед с размерами много большими чем объект исследования.
Расчет произведен на персональном компьютере (ПК) с четырехъядерным центральным процессором (ЦП) 4×2,8 GHz и оперативной памятью 8 GBDDR3.
Для решения уравнений Навье-Стокса (рис. 2), характеризующих физические процессы поведения жидкостей с различными моделями вязкого турбулентного течения [3], была выбрана модель – TurbulentFlowk-ω (турбулентного потока с k-ω интерфейсом уравнений, граничных условий и объемных сил для моделирования течений с турбулентными отрывами) [4].
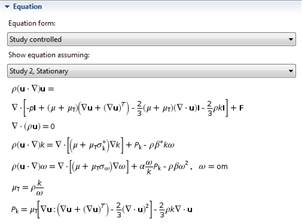
Рисунок 2 – Уравнения Навье-Стокса задачи турбулентности
Для визуализации установившегося стационарного процесса для каждого угла атаки ветряной нагрузки с заданной скоростью произведены расчеты для 129936 степеней свободы, что соответствует 1-2 часам в режиме максимальной производительности ЦП ПК.
На рис. 3 представлено построение сетки, основанное на методе «freetetrahedral» («свободного тетраэдра») с грубым разбиением для объемной расчетной плоскости в виде параллелепипеда с условием калибровки относительно динамики жидкостей и утончённого разбиения рефлектора антеннысовместно с условиями физики твердых тел (127120 элементов сетки).
Для получения наибольшей точности (при конечной визуализации процесса) в областях критичного изменения кривизны поверхности, в кромках геометрических элементов, на стыке конечных форм применяется наиболее уточненное разбиение сетки, что в конечном итоге увеличивает количество уравнений Навье-Стокса.

Рисунок 3– Разбиение расчетной области на сетку в COMSOL Multiphysics
На границах расчетной области использованы условия типа “Inlet” (на входе, задание скорости и направления ветра), “Outlet” (на выходе, устанавливается нормальное давление атмосферы), “Symmetry” (симметричные условия, применены для четырех стенок параллелепипеда с целью задания граничных условий с возможностью проникновения и исчезновения напряжений сдвига).
Результаты расчетов
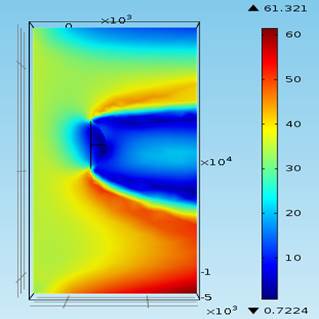
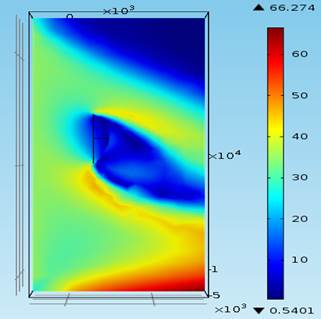
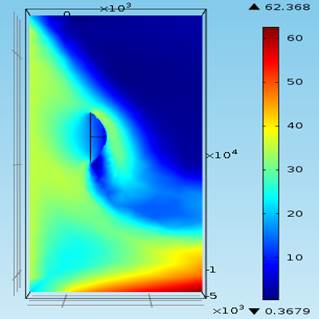
По завершению требуемых количеств итераций расчета получена наглядная картина распределения скорости, давления и возникающей турбулентности вблизи расчетной поверхности рефлектора антенны. По получившимся данным можно сказать, что зеркало антенны является плохообтекаемым аэродинамическим телом, которое характеризуется возникновением “нестабильной” области, обусловленной отрывом пограничного турбулентного слоя с областей резкого изменения кривизны поверхности рефлектора, что, как следствие, приводит к возникновению малых скоростей течения потоков.
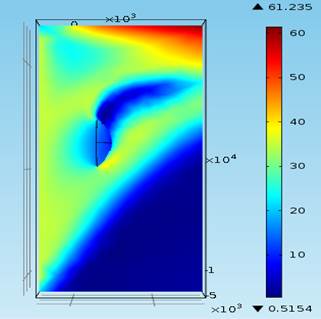
На рис. 4 и рис. 5 представлено распределение скорости ветра (м/с) в вертикальной плоскости сечения XY для различного угла атаки ветра и распределение давления по поверхности рефлектора в вертикальной плоскости XY для угла атаки ветра 900 соответственно.
|
Угол атаки ветра 22,50 |
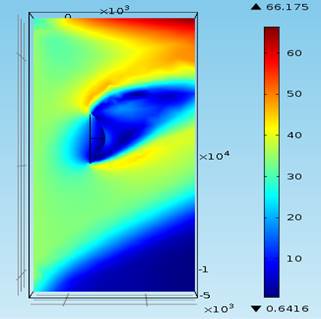
Угол атаки ветра 450 |
|
Угол атаки ветра 67,50 |
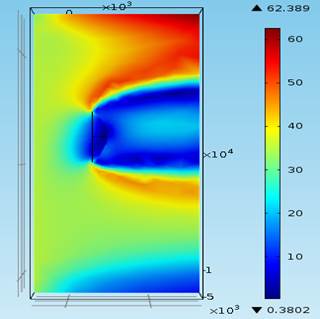
Угол атаки ветра 900 |
|
Угол атаки ветра 112,50 |
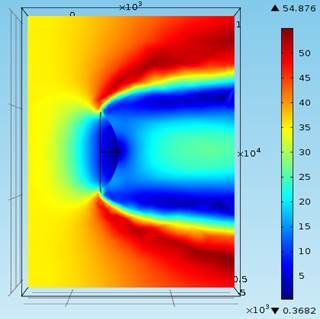
Угол атаки ветра 1350 |
|
Угол атаки ветра 157,50 |
|
Рисунок 4 – Распределение скорости ветра (м/с) в вертикальной плоскости сечения XY для различного угла атаки ветра в диапазоне от 22,50 до 157,50 с шагом 22,50
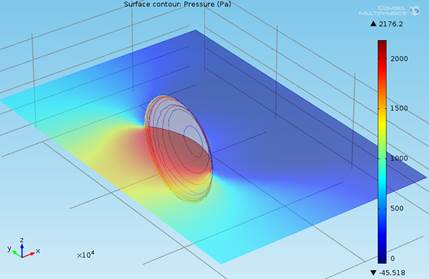
Рисунок 5– Распределение давления по поверхности рефлектора в вертикальной плоскости XY для угла атаки ветра 900
На основании вышеприведенных расчетов распределенных аэродинамических сил и давления выведены формулы для расчета суммарных ветровых нагрузок (вращающий момент и лобовое сопротивление относительно оси вращения антенны).
Все расчеты выполнены в соответствии с геометрией рефлектора антенны в абсолютной системе координат XYZ, ось вращения находится в центре апертуры зеркала и является точкой отсчета, имеющие размерность величины определены в соответствии с радиусом проекции рефлектора S=19.87 м2 (определение лобового сопротивления), а также с учетом радиуса зеркала R=2,250 м (определение вращающего момента).
На рис. 6 представлена зависимость определенных размерных величин ветровой нагрузки (силы в Н, момент – в Н×м) в зависимости от угла атаки (угол в градусах).
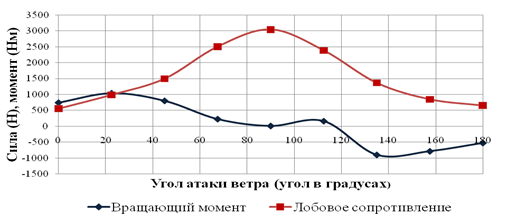
Рисунок 6 – График зависимости определенных размерных величин ветровой нагрузки (силы в Н, момент – в Н·м) в зависимости от угла атаки (угол в градусах)
Анализ результатов и выводы
Определенные ветровые нагрузки, приложенные к рефлектору параболической антенны при изменяющихся углах атаки и скорости ветра 35 м/с, рассчитанные при помощи ПК, позволили выявить основные особенности аэродинамики рефлектора антенны как плохообтекаемого тела и определить значения вращающего момента и лобового сопротивления. Специфическая форма зеркала антенны, выполненная на основе отсеченного параболоида вращения, приводит к появлению эффекта «парусности», и наибольшее значение лобового сопротивления XM=2176 Н выявлено под углом атаки ветра в диапазоне от 800 до 1000, а наименьшее значение наблюдается при “продольном” обтекании рефлектора антенны. Момент My(Н·м), приводящий во вращение зеркало антенны относительно точки отсчета, относительно не большой и меняет свой знак в зависимости от направления ветра, максимальное значение MyM=1042,Н×м лежит в пределах угла атаки ветра равного 22,50.
Полученные результаты необходимы для определения сил трения в механических узлах креплений подвижных частей, а также для нахождения суммарной нагрузки механизма вращения McƩ, действующей на антенну при ее повороте.
Рецензенты:
Кабышев А.В., д.ф.-м.н., старший научный сотрудник, профессор Национального исследовательского Томского политехнического университета, г. Томск.
Лукутин Б.В., д.т.н., профессор, заведующий кафедрой электроснабжения промышленных предприятий Национального исследовательского университета, г. Томск.
Библиографическая ссылка
Сарсикеев Е.Ж., Ляпунов Д.Ю., Бобихов Р.С., Петрусёв А.С. ВИЗУАЛЬНОЕ МОДЕЛИРОВАНИЕ ВЕТРОВОЙ НАГРУЗКИ РЕФЛЕКТОРА ПАРАБОЛИЧЕСКОЙ АНТЕННЫ СВЯЗИ В ПРОГРАММНОМ ПАКЕТЕ COMSOL MULTIPHYSICS // Современные проблемы науки и образования. 2014. № 3. ;URL: https://science-education.ru/ru/article/view?id=13668 (дата обращения: 11.02.2026).