Введение
Перенос электродного металла является важнейшим этапом процесса сварки плавящимся электродом в защитных газах, от которого зависят формирование сварного шва, его технологические свойства и разбрызгивание электродного металла.
Формирование сварного шва и разбрызгивание электродного металла во многом определяются размером переносимых капель; чем меньше капля, тем лучше формирование и качество шва [3; 5]. Время существования капли также влияет на протекание металлургических процессов, в частности, на степень выгорания легирующих элементов: с уменьшением времени существования капли количество легирующих элементов, переходящих из электродной проволоки в наплавленный металл, увеличивается, и за счет этого повышаются механические свойства сварного шва [8].
Цель исследования
Математическое обоснование и определение оптимальных параметров переноса электродного металла для дальнейшего создания синергетических систем управления процессом сварки.
Снижение размера переносимой капли электродного металла повышает качество сварного шва [8], вследствие этого можно сказать, что любые способы, позволяющие снизить размер капли, направлены на повышение качества сварных конструкций.
Размер капли электродного металл непосредственно связан с переносом капли, который, как и всякий механический процесс, связан с затратой энергии, так как при этом нарушается баланс сил, удерживающих каплю на торце электрода. Поэтому при изменении каких-либо параметров необходимо сохранить начальные условия переноса капли электродного металла, т.е. заданное количество энергии, которое зависит от массы капли и скорости ее движения ![]() . Отсюда следует, что масса капли является одним из параметров, определяющих количество энергии, необходимой для переноса капли. Вследствие этого ее снижение без изменения остальных составляющих изменит соотношение сил и вероятность переноса капли в сварочную ванну. Следовательно, для восстановления баланса сил необходимо ввести дополнительную энергию, которая совершит работу против сил, удерживающих каплю на торце электрода.
. Отсюда следует, что масса капли является одним из параметров, определяющих количество энергии, необходимой для переноса капли. Вследствие этого ее снижение без изменения остальных составляющих изменит соотношение сил и вероятность переноса капли в сварочную ванну. Следовательно, для восстановления баланса сил необходимо ввести дополнительную энергию, которая совершит работу против сил, удерживающих каплю на торце электрода.
Эту энергию можно вносить непрерывно в процессе формирования и переноса капли или дискретно, т.е. в определенные моменты времени, от которых зависит процесс переноса. Введение энергии в заданные моменты времени позволяет изменить только те параметры переноса, которые являются ключевыми. А непрерывное введение дополнительной энергии приводит к отрицательному эффекту в моменты времени, когда для достижения положительного результата необходимо снижать количество вводимой энергии. Поэтому только применение импульсных процессов позволяет реализовать оптимальные энергетические параметры. Учитывая, что изменение силы тока ведет к изменению скорости перемещения капли в сторону сварочной ванны, а изменение движения проволоки оказывает влияние на сварочный ток, то можно сказать, что оба процесса имеют идентичное начало [4]. Таким образом, дискретное введение энергии можно реализовать двумя способами – энергетическим и механическим. В первом случае дополнительная энергия вводится в процесс переноса с помощью модуляции сварочного тока, во втором – с помощью модуляции движения сварочной проволоки. При сварке в СО2 наиболее устойчивым процессом является сварка с короткими замыканиями. В этом случае необходимо учитывать, что после образования перемычки между каплей и сварочной ванной переход капли становится необратимым процессом. Таким образом, рассматриваем только те силы, которые действуют на каплю до момента ее касания со сварочной ванной. Поэтому для исследования процесса переноса необходимо определить массу капли, способную перейти в сварочную ванну под действием ускорения свободного падения с учетом злектродинамических сил, сил поверхностного натяжения и давления плазменных потоков. Уравнение основных сил, действующих на каплю:
![]() ,(1)
,(1)
где ![]() - электродинамическая сила, Н;
- электродинамическая сила, Н; ![]() - динамическая сила, которая является суммой силы тяжести и силы инерции, полученной при движении капли, Н;
- динамическая сила, которая является суммой силы тяжести и силы инерции, полученной при движении капли, Н; ![]() - сила давления плазменных потоков, Н;
- сила давления плазменных потоков, Н;![]() - сила поверхностного натяжения, Н.
- сила поверхностного натяжения, Н.
Для решения данного уравнения необходимо определить значения сил и некоторые коэффициенты.
Электродинамическая сила определяется из выражения [9; 10]:
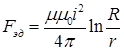 , Н(2)
, Н(2)
где μ – относительная магнитная проницаемость стали, µ = 200; μ0 – магнитная постоянная; i – плазменный ток дуги, А; R – радиус капли, мм; r – радиус проволоки, мм.
Динамическая сила, зависящая от ускорения [7]:
![]() , Н(3)
, Н(3)
где m – масса капли, кг; g – ускорение свободного падения, м/с2; а – ускорение капли, возникающее при остановке проволоки, м/с2.
Сила давления плазменных потоков [10]:
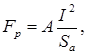 Н (4)
Н (4)
где А - коэффициент, зависящий от материала электрода и параметров приэлектродных областей; I – сила сварочного тока, А; Sa – площадь анодного пятна, мм2.
При определении силы давления плазменных потоков необходимо найти значение коэффициента А для данного вида сварки. Это давление изменяет форму сварочной ванны. Следовательно, для определения коэффициента А при сварке в среде СО2 рассмотрим кадр скоростной киносъемки (рис. 1а) и по нему определим изменение формы ванны, сделав допущение, что видимая ее форма является истинной. По точкам, снятым с кадра скоростной киносъемки, путем аппроксимации построим кривую, представленную на рис. 1б.
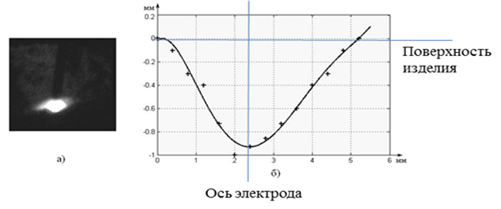
Рис. 1. Изменение глубины сварочной ванны при сварке в СО2 проволокой Св-08Г2С dэл = 1.2 мм на режиме I = 180 А, U = 28 В: а) фотография дуги; б) аппроксимация полученных точек.
Данная кривая позволяет определить граничные условия для расчета давления сварочной дуги и изменения его относительно центра кратера. Для расчета силового воздействия сварочной дуги используем выражение нормального распределения силового воздействия [1]:
![]() , Н(5)
, Н(5)
где Pmax – максимальное давление в центре кратера Па; k – коэффициент сосредоточенности давления; R – радиальная координата.
В каждой координате сила давления будет зависеть от силы поверхностного натяжения сварочной ванны, поэтому можно сказать, что для каждой точки ![]() , где z – глубина сварочной ванны в данной координате. Следовательно, силу давления дуги можно рассчитать, как интеграл по поверхности ее кратера. Кривая поверхности кратера приблизительно описывается трансцендентной показательной функцией [2]:
, где z – глубина сварочной ванны в данной координате. Следовательно, силу давления дуги можно рассчитать, как интеграл по поверхности ее кратера. Кривая поверхности кратера приблизительно описывается трансцендентной показательной функцией [2]:
![]() (6)
(6)
где b – глубина кратера по осевой линии, равная![]() ;
; ![]() , х – радиус кратера сварочной дуги, мм. Таким образом, произведение интеграла выражения (6) на коэффициент поверхностного натяжения сварочной ванны является силой давления сварочной дуги:
, х – радиус кратера сварочной дуги, мм. Таким образом, произведение интеграла выражения (6) на коэффициент поверхностного натяжения сварочной ванны является силой давления сварочной дуги:
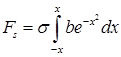 , Н(7)
, Н(7)
Известно [10], что коэффициент поверхностного натяжения для жидкой стали, в зависимости от температуры, изменяется в пределах ![]() Н/м. Учитывая, что сварка в СО2 ведется на повышенной плотности тока, берем максимальное значение коэффициента и получаем силу давления сварочной дуги для данного случая Fs = 0,23 H. Тогда из выражения (4) коэффициент А будет равен:
Н/м. Учитывая, что сварка в СО2 ведется на повышенной плотности тока, берем максимальное значение коэффициента и получаем силу давления сварочной дуги для данного случая Fs = 0,23 H. Тогда из выражения (4) коэффициент А будет равен:
![]() (8)
(8)
и с учетом начальных условий (I =180 A, S = 1,47 мм2) для сварки в СО2 проволокой Св-08Г2С 1,225∙10-5 Н·мм2/А2. Используя полученный коэффициент, построена номограмма зависимости давления сварочной дуги от тока и диаметра сварочной проволоки, которая представлена на рис. 2.
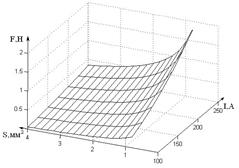
Рис. 2. Номограмма изменения давления плазменных потоков в зависимости от силы сварочного тока и диаметра проволоки.
Сила поверхностного натяжения между каплей и сварочной ванной, зависящая от диаметра проволоки:
![]() , Н(9)
, Н(9)
где σ – коэффициент поверхностного натяжения, Н/м.
Введя значение сил в выражение (1) и разделив их на ускорение свободного падения, получим массу капли, способную перейти в сварочную ванну при сварке с короткими замыканиями:
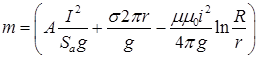 , кг(10)
, кг(10)
Теперь, задав начальные условия, можно рассчитать размер капли электродного металла, способной перейти в сварочную ванну под действием сил (10) при заданных начальных условиях. Начальные условия - диаметр наиболее применяемой сварочной проволоки d = 1,2 мм, падение напряжения на дуге Uд = 28 В, сварочный ток I = 180 А. Размер капли, необходимый для расчета электродинамической силы, определяем из кадра киносъемки, представленного на рис. 3а.
Из представленного кадра определяем, что для данных условий ![]() , и таким образом, подставив в выражение (10) известные данные, получаем m = 0,0315 г.
, и таким образом, подставив в выражение (10) известные данные, получаем m = 0,0315 г.
Проведенные измерения показывают, что задав радиус капли R ≈ 1,7r и зная, что при температуре Т = 1530 С плотность жидкой стали ρ = 7,23 г/мм3, получаем массу капли m ≈ 0,0321 г, что составляет разницу с расчетной на 1,9%.
Имея значение массы капли, способной перейти в сварочную ванну при заданных начальных условиях, можно переходить к расчетам ее изменения при изменении энергетических параметров.
Первоначально рассмотрим изменение массы капли в зависимости от сварочного тока. Ток, протекающий в системе «сварочная проволока – жидкая капля – сварочная дуга – сварочная ванна», вызывает появление магнитного поля и возникновение электродинамической силы, которая способствует переносу капли в сварочную ванну.
Как можно заметить из выражения (2), уменьшение радиуса капли R снижает Fэд, поэтому для переноса необходимо ее компенсировать увеличением тока во время импульса, в результате чего энергия капли восстанавливается.
Теперь, приняв допущение, что плазменный ток равен току сварочной дуги, можно определить изменение массы капли в зависимости от тока. На основании этих данных построена номограмма (рис. 4), которая отражает изменения массы капли электродного металла при изменении силы тока от 180 до 360 А. При этом происходит снижение массы капли, способной перейти в сварочную ванну.
Рис. 3. Кинокадр касания капли со сварочной ванной при сварке в СО2 проволокой Св-08Г2С, d = 1,2 мм, I = 180А.
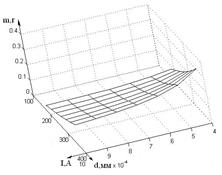
Рис. 4. Номограмма зависимости массы капли от изменения сварочного тока и радиуса капли для проволоки d = 1,2 мм.
Вводя полученные значения изменения электродинамической силы, получим значения массы капли, которая под действием осевой составляющей Fэл преодолевает давление плазменных потоков, касается сварочной ванны и переходит в нее. Получено, что при увеличении силы тока во время импульса при заданных параметрах масса капли, способной перейти в сварочную ванну, снижается от 0,0315 до 0,0136 г.
Теперь рассмотрим влияние динамических сил (3), действующих на каплю при механической модуляции, которые создают результирующую силу, способствующую отрыву капли. Из этого выражения видно, что уменьшение массы капли можно компенсировать увеличением ускорения ее движения.
Приняв начальное ускорение движения капли за ноль, как при сварке с непрерывной подачей проволоки, и подставив это ускорение в выражение (11), можно вычислить Fд, необходимую для отрыва капли при начальных условиях Fд = 4,15·10-4 Н. Сделав допущение, что остальные силы, действующие в сварочной дуге, при изменении ускорения движения капли остаются постоянными, и приняв ![]() , можно определить зависимость
, можно определить зависимость ![]() , которая про увеличении ускорения от 9,8 до 80 м/с2 изменяется m = 0,0322 – 0,0045 г. Таким образом, при сохранении равновесия, согласно выражению (2.4.8), увеличение ускорения способствует снижению массы капли.
, которая про увеличении ускорения от 9,8 до 80 м/с2 изменяется m = 0,0322 – 0,0045 г. Таким образом, при сохранении равновесия, согласно выражению (2.4.8), увеличение ускорения способствует снижению массы капли.
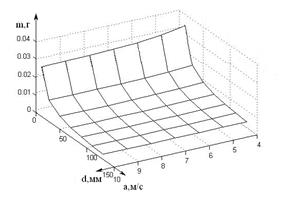
Рис. 5. Номограмма зависимости массы капли от изменения ускорения движения капли и ее радиуса для проволоки d = 1,2 мм.
Номограмма, представленная на рис. 5, позволяет определить изменения допустимого размера капли электродного металла в зависимости от ее ускорения.
Как видно из этой номограммы, увеличение ускорения движения капли способствует снижению размера капли, способной перейти в сварочную ванну. Следовательно, импульсная подача сварочной проволоки, так же как и импульс сварочного тока, создает возможность снижения размера капли электродного металла.
Материал и методы исследования
Для определения необходимых энергетических параметров в исследовании использовались: камера скоростной видеосъемки «Видеоспринт» (частота съемки 500-50000 кадр/с); регистратор параметров сварки AWR - 224M, предназначенный для измерения, отображения и запоминания напряжения на дуге и тока сварки для получения протокола процесса; установка автоматической сварки, укомплектованная механизмом импульсной подачи электродной проволоки на базе ГСП-2 с источником питания ВДГ401.4.
Вывод
Данная методика позволяет задавать оптимальный шаг подачи проволоки в зависимости от режимов сварки и характеристик подающего механизма.
Рецензенты:
Сапожков С.Б., д.т.н., профессор, заведующий кафедрой естественно-научного образования, Юргинский технологический институт (филиал) ФГБОУ ВПО «Национальный исследовательский Томский политехнический университет», г. Юрга.
Петрушин С.И., д.т.н., профессор кафедры «Технология машиностроения», Юргинский технологический институт (филиал) ФГБОУ ВПО «Национальный исследовательский Томский политехнический университет», г. Юрга.
Библиографическая ссылка
Солодский С.А., Луговцова Н.Ю., Горлов Д.С. ОПРЕДЕЛЕНИЕ ЭНЕРГЕТИЧЕСКИХ ПАРАМЕТРОВ ПРОЦЕССА ФОРМИРОВАНИЯ ШВА ПРИ СВАРКЕ В ЗАЩИТНЫХ ГАЗАХ // Современные проблемы науки и образования. 2014. № 3. ;URL: https://science-education.ru/ru/article/view?id=13642 (дата обращения: 11.02.2026).



