Построение расписаний для решения различного типа задач всегда будет актуально, так как главными требованиями к результатам деятельности являются эффективное распределение имеющихся ресурсов и достижение поставленных целей в допустимые сроки. В некоторых специфических видах планирования в качестве одного из ресурсов выступает группа исполнителей или команда специалистов, подготовленных для выполнения особых нестандартных мероприятий. К таким задачам относятся: спасение людей с затонувшей подлодки водолазами-глубоководниками с применением глубоководного водолазного комплекса [3], пилотируемые полеты в космос [6], формирование комплекса целенаправленных действий членов экипажа по повышению эффективности управления воздушным судном [8]. В данной статье предлагается математическая модель составления таких расписаний на примере подготовки планов действий экипажа Российского сегмента (РС) Международной космической станции (МКС) [4; 7] и результаты ее исследования с применением модифицированного генетического алгоритма.
Задан горизонт планирования ![]() , где
, где ![]() - границы интервала,
- границы интервала, ![]() - множество моментов времени в рамках
- множество моментов времени в рамках ![]() с дискретностью, равной 5 минутам [5], где
с дискретностью, равной 5 минутам [5], где ![]() - идентификатор момента времени,
- идентификатор момента времени, ![]() - общее количество моментов времени. Заявленное множество полетных операций выразим через
- общее количество моментов времени. Заявленное множество полетных операций выразим через ![]() , где
, где ![]() - идентификатор полетной операции,
- идентификатор полетной операции, ![]() - количество полетных операций. Группу космонавтов обозначим с помощью множества
- количество полетных операций. Группу космонавтов обозначим с помощью множества ![]() , где
, где ![]() - идентификатор космонавта,
- идентификатор космонавта, ![]() - количество космонавтов. Длительность полетных операций представим в виде множества
- количество космонавтов. Длительность полетных операций представим в виде множества ![]() , где
, где ![]() - длительность операции
- длительность операции ![]() .
. ![]() - матрица моментов времени
- матрица моментов времени ![]() , кратных 5 минутам, в которые операция
, кратных 5 минутам, в которые операция ![]() может быть запланирована оператором, где
может быть запланирована оператором, где ![]() .
. ![]() - матрица моментов времени
- матрица моментов времени ![]() , кратных 5 минутам, в которые космонавт
, кратных 5 минутам, в которые космонавт ![]() имеет возможность выполнять назначенные ему операции, где
имеет возможность выполнять назначенные ему операции, где ![]() .
.
Ресурсы, требуемые для выполнения работ, представлены множеством ![]() , где
, где ![]() - идентификатор ресурса, а
- идентификатор ресурса, а ![]() - общее количество всех видов ресурсов. Количество каждого вида ресурса
- общее количество всех видов ресурсов. Количество каждого вида ресурса ![]() в каждый момент времени
в каждый момент времени ![]() хранится во множестве
хранится во множестве ![]() . Для хранения информации о том, что операция
. Для хранения информации о том, что операция ![]() требует определенного объема ресурса вида
требует определенного объема ресурса вида ![]() , введем множество
, введем множество ![]() . Помимо тех ресурсов, которые можно выразить количественно, есть специального типа ресурсы, обозначенные множеством
. Помимо тех ресурсов, которые можно выразить количественно, есть специального типа ресурсы, обозначенные множеством ![]() , где
, где ![]() - идентификатор специального ресурса, а
- идентификатор специального ресурса, а ![]() - общее количество всех специальных ресурсов. Ресурсы из
- общее количество всех специальных ресурсов. Ресурсы из ![]() в известные моменты времени могут быть либо доступны, либо нет. Для определения моментов, когда тот или иной вид ресурса
в известные моменты времени могут быть либо доступны, либо нет. Для определения моментов, когда тот или иной вид ресурса ![]() можно использовать, введем матрицу
можно использовать, введем матрицу ![]() , где
, где ![]() . Матрица
. Матрица ![]() показывает необходимость задействования спецресурсов операциями, где
показывает необходимость задействования спецресурсов операциями, где ![]() .
.
Среди всего множества операций ![]() есть такие сочетания пар работ, которые нельзя выполнять в одно и то же время. Такие операции называют несовместимыми, и представлены они множеством
есть такие сочетания пар работ, которые нельзя выполнять в одно и то же время. Такие операции называют несовместимыми, и представлены они множеством ![]() , где
, где ![]() . Множество
. Множество ![]() вводится в целях фиксации признака обязательного включения операции
вводится в целях фиксации признака обязательного включения операции ![]() в итоговый план, где
в итоговый план, где ![]() . Множество
. Множество ![]() содержит информацию о том, к какой зоне (бытовой, рабочей) принадлежит операция,
содержит информацию о том, к какой зоне (бытовой, рабочей) принадлежит операция, ![]() .
.
В процессе подготовки космонавтов на тренажерах ими отрабатывается весь комплекс мероприятий, который они будут выполнять на станции. При этом выясняются такие важные моменты, как:
1) кто из космонавтов и какую работу делает более эффективно, корректно, в кратчайшие сроки;
2) как сказывается усталость космонавта на эффективности выполнения одной и той же операции в различное время суток.
Данные показатели в итоге можно свести к количественному виду и определить в диапазоне от 0 до 1, а затем использовать при распределении операций между членами экипажа. Для хранения данной исходной информации введем трехмерную матрицу ![]() , где элемент
, где элемент ![]() - показатель (коэффициент) эффективности реализации операции
- показатель (коэффициент) эффективности реализации операции ![]() членом экипажа
членом экипажа ![]() , начатой им в момент времени
, начатой им в момент времени ![]() . Причем значение
. Причем значение ![]() в том случае, когда космонавт
в том случае, когда космонавт ![]() максимально эффективно выполняет операцию
максимально эффективно выполняет операцию ![]() в момент времени
в момент времени ![]() .
.
Многие работы из ![]() связаны между собой временными отношениями. Поэтому обозначим эти связи, используя граф отношений предшествования
связаны между собой временными отношениями. Поэтому обозначим эти связи, используя граф отношений предшествования ![]() , где
, где ![]() - множество вершин, а
- множество вершин, а ![]() - множество дуг. Запись вида
- множество дуг. Запись вида ![]() содержит информацию о том, что операция
содержит информацию о том, что операция ![]() должна начинаться не раньше, чем момент начала операции
должна начинаться не раньше, чем момент начала операции ![]() плюс смещение по времени величиной
плюс смещение по времени величиной ![]() .
.
Каждая полетная операция характеризуется типом приоритета. Приоритет может быть фиксированный и переменный. Величина фиксированного приоритета не меняется на протяжении всего интервала планирования. Значение же переменного приоритета может быть различным в зависимости от того, в какой момент времени ![]() операция
операция ![]() запланирована. Максимальное значение переменного приоритета достигается в том случае, если на протяжении всего промежутка времени, в течение которого выполняется операция, удовлетворены все условия ее успешного завершения. Будем считать, что в качестве исходных данных для каждой операции известны тип приоритета и величина фиксированного приоритета, а для переменного – максимально возможное значение, достижимое внутри заданного
запланирована. Максимальное значение переменного приоритета достигается в том случае, если на протяжении всего промежутка времени, в течение которого выполняется операция, удовлетворены все условия ее успешного завершения. Будем считать, что в качестве исходных данных для каждой операции известны тип приоритета и величина фиксированного приоритета, а для переменного – максимально возможное значение, достижимое внутри заданного ![]() . Введем множество
. Введем множество ![]() , где элемент
, где элемент ![]() является кортежем из двух составляющих
является кортежем из двух составляющих ![]() . Здесь
. Здесь ![]() , а
, а ![]() - предел величины приоритета, к которому следует стремиться при размещении операций в плане.
- предел величины приоритета, к которому следует стремиться при размещении операций в плане.
На основе вышеприведенных исходных данных следует подготовить расписание таким образом, чтобы минимизировать описанные ниже критерии оптимизации и удовлетворить ограничениям. Для этого введем трехмерную матрицу ![]() , где элемент
, где элемент ![]() - бинарная переменная,
- бинарная переменная, ![]() . В процессе расчетов, а после и в момент завершения подготовки расписания, необходимо иметь представление о конечном состоянии всего множества ресурсов
. В процессе расчетов, а после и в момент завершения подготовки расписания, необходимо иметь представление о конечном состоянии всего множества ресурсов ![]() . Для этого обозначим общий баланс каждого вида ресурса
. Для этого обозначим общий баланс каждого вида ресурса ![]() в каждый момент времени
в каждый момент времени ![]() в виде матрицы
в виде матрицы ![]() , где
, где ![]() - количество используемого ресурса
- количество используемого ресурса ![]() в момент времени
в момент времени ![]() , потребляемое всеми операциями, которые выполняются в этот самый момент времени
, потребляемое всеми операциями, которые выполняются в этот самый момент времени ![]() .
.
Для выполнения расчетов целесообразно ввести множество ![]() значений приоритетов всех размещенных в плане операций. Здесь
значений приоритетов всех размещенных в плане операций. Здесь 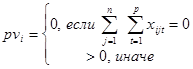 .
.
В качестве критериев подготовки оптимальных планов распределения полетных операций между космонавтами предлагаются следующие три критерия. Первый критерий – минимизация простоев исполнителей:
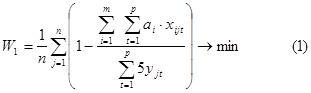
Второй критерий представляет собой распределение операций между исполнителями таким образом, чтобы минимизировать случаи их неэффективного выполнения:
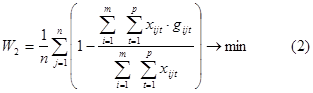
Для включения в план в первую очередь самых необходимых полетных операций следует учитывать их приоритет. Поэтому третий критерий можно представить, как включение в план операций с наибольшим значением фиксированного приоритета и операций с переменным приоритетом, но обеспечить их расположение внутри плана таким образом, чтобы величина переменного приоритета принимала максимальное значение. Формализация критерия представлена в виде:
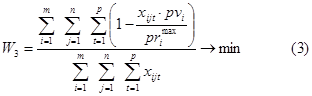
Одним из способов сведения данной постановки задачи с тремя критериями к однокритериальному виду является аддитивная свертка с весовыми коэффициентами, которые определяются группой экспертов:
![]()
Поскольку достигнуть оптимума по каждому частному критерию при одном и том же решении ![]() вряд ли возможно, следует в качестве эффективного
вряд ли возможно, следует в качестве эффективного ![]() выбирать такое, которое дает минимальное относительное отклонение оптимальных значений по всем частным критериям в соответствии с заданным предпочтением в виде весовых коэффициентов
выбирать такое, которое дает минимальное относительное отклонение оптимальных значений по всем частным критериям в соответствии с заданным предпочтением в виде весовых коэффициентов ![]() . Решение
. Решение ![]() не является альтернативным, если оно нарушает предельно допустимые границы относительной погрешности критериев (1) – (3), составляющие для
не является альтернативным, если оно нарушает предельно допустимые границы относительной погрешности критериев (1) – (3), составляющие для ![]() -15%, для
-15%, для ![]() -10%, для
-10%, для ![]() -10%.
-10%.
Для расчетов переменного приоритета, используемого в (3), необходимо ввести промежуточную матрицу ![]() , где элемент
, где элемент ![]() - значение переменного приоритета операции
- значение переменного приоритета операции ![]() , начатой в момент времени
, начатой в момент времени ![]() . Для расчета значения
. Для расчета значения ![]() предлагается представить его в виде функции от нескольких переменных:
предлагается представить его в виде функции от нескольких переменных:
![]()
где приведенные аргументы имеют следующую смысловую нагрузку:
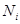 - оценка важности операции
- оценка важности операции 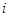 относительно других операций в исходном наборе;
относительно других операций в исходном наборе; 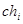 - оценка частоты проведения операции
- оценка частоты проведения операции 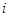 с учетом выполнения всех требований;
с учетом выполнения всех требований; 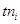 - оценка наступления рекомендуемого времени проведения операции
- оценка наступления рекомендуемого времени проведения операции 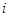 в плане;
в плане; 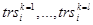 - оценки удовлетворения требуемым условиям проведения операции
- оценки удовлетворения требуемым условиям проведения операции 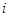 в конкретном месте интервала планирования по
в конкретном месте интервала планирования по 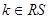 специальным ресурсам;
специальным ресурсам; 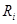 - оценка ресурсов
- оценка ресурсов 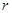 , необходимых для выполнения операции
, необходимых для выполнения операции 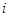 , по отношению к общему остатку ресурсов
, по отношению к общему остатку ресурсов 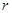 на станции.
на станции.
Данные об аргументах, влияющих на переменный приоритет, заносятся в матрицу ![]() , где
, где ![]() - порядковый номер аргумента, а
- порядковый номер аргумента, а ![]() - количество аргументов в (5). Элемент матрицы представлен кортежем из трех составляющих
- количество аргументов в (5). Элемент матрицы представлен кортежем из трех составляющих ![]() , где
, где ![]() - значение рассчитанного аргумента
- значение рассчитанного аргумента ![]() для рабочей операции
для рабочей операции ![]() в момент времени
в момент времени ![]() ,
, ![]() - значение весового коэффициента, назначенного экспертами для аргумента
- значение весового коэффициента, назначенного экспертами для аргумента ![]() рабочей операции
рабочей операции ![]() ,
, ![]() - признак того, что это основной аргумент или нет,
- признак того, что это основной аргумент или нет, ![]() .
.
Все указанные выше оценки сводятся в одну, которая представляет переменный приоритет рабочей операции ![]() в момент времени
в момент времени ![]() , отражающий ее проведение в данном месте интервала планирования в данное время. Формула для расчета переменного приоритета рабочей операции
, отражающий ее проведение в данном месте интервала планирования в данное время. Формула для расчета переменного приоритета рабочей операции ![]() имеет следующее математическое представление:
имеет следующее математическое представление:
![]()
где ![]() – фактор, рассчитываемый на основании значения основного аргумента, у которого
– фактор, рассчитываемый на основании значения основного аргумента, у которого ![]() , и
, и 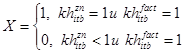 . Таким образом, при частичном выполнении главного условия проведения операции (основной аргумент), ее переменный приоритет в данном месте интервала планирования равен 0.
. Таким образом, при частичном выполнении главного условия проведения операции (основной аргумент), ее переменный приоритет в данном месте интервала планирования равен 0.
Для определения факта задействования интересующего нас космонавта в реализации конкретной работы в заданный момент времени введем алгоритмически вычисляемую функцию от трех переменных ![]() . Итоговый допустимый план должен удовлетворять следующим условиям и ограничениям:
. Итоговый допустимый план должен удовлетворять следующим условиям и ограничениям:
1) суммарное количество любого вида ресурса ![]() в момент времени
в момент времени ![]() , используемого всеми запланированными полетными операциями в совокупности, не должно превышать значения, имеющегося на борту:
, используемого всеми запланированными полетными операциями в совокупности, не должно превышать значения, имеющегося на борту:
![]()
2) в течение всего горизонта планирования каждая операция может быть выполнена одним членом экипажа не более одного раза:
![]()
3) проверка корректности соблюдения временных отношений между полетными операциями:
![]()
4) условие наличия в плане всех обязательных операций:
![]()
5) условие соответствия общей продолжительности выполнения операций в плане, назначенных исполнителю ![]() , величине суммарного времени функционирования этого исполнителя:
, величине суммарного времени функционирования этого исполнителя:
![]()
6) как и в любой системе планирования, где один прибор не может одновременно обрабатывать несколько деталей, так и один член команды не должен одновременно делать более одной операции:
![]()
7) отсутствие одновременной реализации в плане несовместимых полетных операций:
![]()
8) условие выполнения норм РТО, а именно соблюдение границ рабочей и бытовой зон. Необходимо ввести два параметра: ![]() - закрепленная нормативными документами максимальная продолжительность рабочей зоны для одного исполнителя,
- закрепленная нормативными документами максимальная продолжительность рабочей зоны для одного исполнителя, ![]() - продолжительность бытовой зоны для одного исполнителя. Получаем два неравенства:
- продолжительность бытовой зоны для одного исполнителя. Получаем два неравенства:
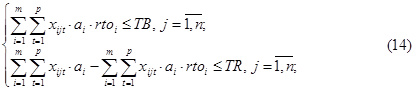
Поставленная задача была решена с применением аппарата генетических алгоритмов. Данный эвристический подход позволяет находить решение NP-трудных задач за приемлемое время [9], что особенно важно на этапах оперативного планирования. Для соответствия условиям поставленной задачи и математической модели была проведена модификация простого генетического алгоритма (ПГА), описанного Д. Гольдбергом на основе работ Д. Холланда [2]. Реализация механизма ПГА заключается в следующих этапах:
- случайно генерируется популяция последовательностей (альтернативных решений), используется бинарное кодирование;
- для селекции используется подход на основе колеса рулетки;
- для скрещивания используется оператор одноточечного кроссинговера;
- выполняется оператор мутации;
- создается следующее поколение (новая генерация) путем полной замены родителей потомками.
Модификация приведенного выше механизма ПГА для поставленной задачи заключается в следующих особенностях:
- применение как бинарного, так и вещественного кодирования хромосом;
- скрещивание между собой каждого подмножества операций одного класса важности в составе двух последовательностей (вещественное кодирование) с использованием кроссовера ОХ [1];
- формирование одного потомка из всех родителей путем поочередного соединения предварительно выделенных лучших подмножеств операций по каждому классу важности и последующее включение его в новую популяцию;
- применение к кодировкам, полученным после проведения процедуры скрещивания, специального механизма группировки операций, имеющих отношения предшествования;
- направленный характер мутации хромосом с вещественным кодированием путем случайного замещения одного блока операций, имеющих отношения предшествования, на другой блок связанных работ;
- формирование новой популяции на основе репродукции устойчивого состояния.
На каждой итерации разработанного генетического алгоритма для формирования допустимых планов последовательно решаются две задачи:
- Первая задача заключается в построении уникальных последовательностей, задающих порядок размещения операций друг за другом на основе информации о характеризующем операцию классе важности относительно остальных работ. Структура хромосомы, используемая для решения данной проблемы, представлена на рисунке 1а.
- Смысл второй задачи состоит в определении момента начала реализации каждой операции внутри интервала планирования для всех сформированных ранее уникальных последовательностей, а также в выборе реализующих эту операцию специалистов. На рисунке 1б описана структура хромосомы, подобранная для решения данной задачи.

Рисунок 1. Представление хромосом в модифицированном генетическом алгоритме.
Для определения в целом возможности применения разработанного алгоритма для планирования действий экипажа, а также оценки эффективности его результатов, был проведен эксперимент. Для каждого набора операций было проведено по два типа испытаний – формирование плана с заданным набором операций сначала осуществлялось непосредственно оператором, а затем этот же план рассчитывался с использованием модифицированного генетического алгоритма. Испытания проводились на одном и том же интервале планирования, равном 24 часам, для 9 различных наборов данных, где в первом наборе было 40 операций, а в каждом последующем на 10 операций больше. Наборы из 40, 50, 60 и 70 операций распределялись между 3 исполнителями, а наборы из 80, 90, 100, 110 и 120 операций – между шестью исполнителями.
В качестве результатов для подведения итогов эксперимента рассматривались два параметра:
- время, за которое оператор или генетический алгоритм завершит размещение операций между исполнителями;
- количество операций из набора, которые удалось разместить корректно внутри заданного горизонта планирования.
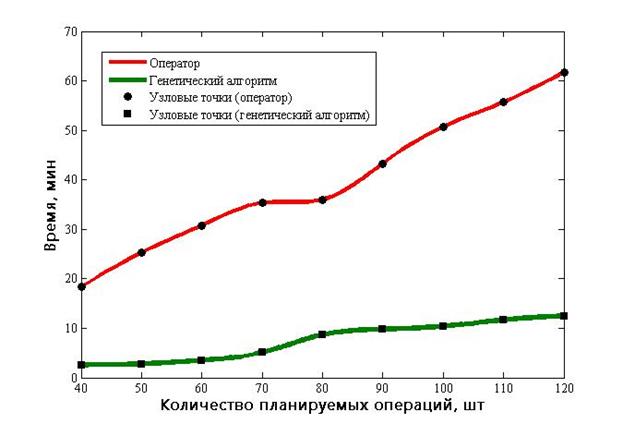
Рисунок 2. Результаты распределения операций непосредственно оператором и модифицированным генетическим алгоритмом.
Из графика на рисунке 2 видно, что применение модифицированного генетического алгоритма позволило найти допустимое решение в среднем в 6 раз быстрее по сравнению с оператором.
Вторым важным показателем является то количество операций из каждого набора, которые размещены в плане корректным образом, то есть в тех моментах времени, когда соблюдаются все условия и правила для их успешного выполнения. Следует заметить, что оператору с учетом его опыта и профессионализма удалось разместить полностью все операции из каждого набора. На рисунке 3 приведены результаты работы генетического алгоритма в виде столбчатой диаграммы. Высота каждого столбца диаграммы отражает процент корректно размещенных на горизонте планирования операций из соответствующего набора. Внутри каждого столбца находится число, равное количеству верно размещенных операций из каждого набора в итоговом плане. Так, например, для плана из 110 работ генетический алгоритм не запланировал лишь 4 операции, а 106 операций разместил верно. Таким образом, диаграмма показывает, что в допустимых планах, подготовленных алгоритмом, как минимум 90% операций размещены согласно правилам и условиям их эффективной реализации.
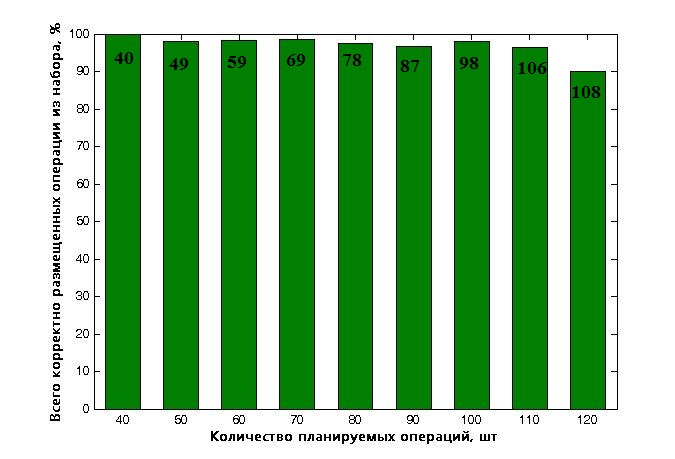
Рисунок 3. Количество корректно размещенных операций из каждого набора в итоговом плане, сформированном генетическим алгоритмом.
Проведенный эксперимент подтверждает возможность применения математической модели и разработанного модифицированного генетического алгоритма непосредственно при составлении планов. Особенно данная разработка будет полезна при срочных процедурах перепланирования, когда оператор должен исправить план в кратчайшие сроки. С учетом значительного сокращения времени оператор получает допустимый план, уже проверенный на все основные ограничения, а количество корректно размещенных в нем операций в среднем достигает 97%.
Эффективность применения модифицированного генетического алгоритма к поставленной задаче заключается в значительном сокращении времени на подготовку допустимого плана и в высоком показателе корректно запланированных операций, что говорит о качестве итогового плана. При таком механизме работы планировщику необходимо лишь проверить полученный итоговый план, что займет у него совсем немного времени. С другой стороны, применение модели и алгоритма формирования субоптимальных планов позволяет действительно оперативно решать задачи перепланирования и предоставляет оператору значительное количество дополнительных минут для выполнения не менее важных поручений, связанных с его ежедневной деятельностью.
Рецензенты:
Седов А.В., д.т.н., профессор кафедры «Автоматика и телемеханика» ФГБОУ ВПО «Южно-Российский государственный политехнический университет (НПИ) имени М.И. Платова», г.Новочеркасск.
Кобак В.Г., д.т.н., профессор кафедры «Программное обеспечение вычислительной техники и автоматизированных систем» ФГБОУ ВПО «Донской государственный технический университет», г. Ростов-на-Дону.
Библиографическая ссылка
Орловский Н.М. ИССЛЕДОВАНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ФОРМИРОВАНИЯ ОПТИМАЛЬНЫХ ПЛАНОВ ФУНКЦИОНИРОВАНИЯ ГРУППЫ СПЕЦИАЛИСТОВ // Современные проблемы науки и образования. 2014. № 3. ;URL: https://science-education.ru/ru/article/view?id=13639 (дата обращения: 11.02.2026).



