В настоящее время Министерством образования и науки представлен для обсуждения проект концепции и содержания профессионального стандарта педагога (далее проект стандарта) [5]. Этот документ, по утверждению разработчиков, направлен на повышение качества профессиональной деятельности учителей путем установления единых требований и критериев оценивания уровня их квалификации. Очевидно, эти требования и критерии должны найти адекватное отражение и в содержании федеральных государственных образовательных стандартов высшего педагогического образования (ФГОС ВПО), и в реальной практике подготовки учителей в педвузах.
Проанализировав предметные и профессиональные компетенции учителя, предлагаемые в проекте стандарта, мы выделили те, которые связаны с обучением школьников практическим приложениям математики. Согласно этому документу, учитель математики должен:
-
в области предметных компетенций «иметь представление о широком спектре приложений математики и знать доступные учащимся математические элементы этих приложений»;
-
в области профессиональных компетенций «…совместно с учащимися анализировать учебные и жизненные ситуации, в которых можно применить математический аппарат и математические инструменты, то же – для идеализированных (задачных) ситуаций, описанных текстом...». «Содействовать мотивации и результативности каждого учащегося, используя такие свойства предмета, как: … объяснение и предсказание реальности» [5].
Процитированные положения подтверждают практическую ориентацию современного школьного математического образования, отраженную в современных ФГОС, и задают направление методической подготовки педагога. Однако предлагаемые компетенции носят довольно общий характер, что не позволяет использовать их для оценки деятельности учителя математики. Для их конкретизации необходимы выделение содержания и путей реализации практико-ориентированного обучения математике в школе, а также разработка соответствующей методической системы подготовки учителя. Предлагаемая нами модель методической системы подготовки учителя к практико-ориентированному обучению математике в школе позволит определить критерии оценивания профессиональной деятельности учителя в этом направлении.
Использование в обучении математике ее практических приложений является специфической особенностью российского школьного математического образования. Анализ исторических документов, содержания учебников разных лет показывает, что в обучении математике в школе всегда использовались ее приложения. Первоначально содержание образования было нацелено на подготовку обучающихся к определенной профессиональной деятельности, т.е. носило контекстный характер. Об этом свидетельствует появление в 1701 году «Школы математических и навигацких наук», где математика была разделена на теоретическую (чистую) и практическую (прикладную), показывающую пути применения математических знаний в мореходном деле [4]. Приложения математики здесь предстают в виде рецептов разрешения конкретных ситуаций. В настоящее время, пройдя периоды трудовой школы, политехнической и прикладной направленности обучения, математическое образование приобретает черты общекультурной значимости, что предполагает его направленность на приобретение школьниками конкретных, осознанных представлений о значении математики как науки в различных областях действительности. Современные предметные результаты изучения математики, в частности, включают «формирование представлений о математике как о методе познания действительности, позволяющем описывать и изучать реальные процессы и явления» [6].
Несмотря на признание на современном этапе необходимости обучения школьников приложениям математики, существует ряд препятствий, не позволяющих в полной мере реализовать в школе практико-ориентированное обучение математике. Основными из них являются следующие:
-
Не уделяется должного внимания методической подготовке учителя к обучению школьников практическим приложениям математики в педвузе.
-
Недостаточно разработаны теория и методика обучения школьников практическим приложениям математики в связи с задачами, поставленными во ФГОС общего образования. Нет концептуальной и методической ясности в вопросе о том, в какой форме и объеме приложения математики целесообразно включить в обязательную программу школьного курса.
-
Нет достаточного количества современных методических и учебных пособий для учителей и учащихся, содержание которых ориентировано на планомерное осуществление практико-ориентированного обучения математике в школе.
Как справедливо утверждают авторы проекта стандарта, «от педагога нельзя требовать то, чему его никто никогда не учил» [5]. Поэтому, исходя из выявленных проблем, есть необходимость разработки методической системы подготовки учителя к практико-ориентированному обучению математике в школе, которая является подсистемой всей системы профессиональной подготовки учителя математики. Нами определены компоненты такой системы: целевой, содержательный, методический и результативно-оценочный.
Для обоснования состава целевого компонента представим сначала содержательный и методический компоненты системы. Содержательный компонент состоит из трех модулей: методологического, исторического и методического. Методологический модуль включает вопросы, освещающие методологию процесса применения математики к изучению окружающей действительности, в том числе и на уровне обучения школьников. Исторический модуль содержит сведения, формирующие представления у студентов об исторических, а также социальных и культурных факторах становления школьного математического образования в области приложений математики в разные временные периоды. Содержание методического модуля ориентировано на подготовку студентов к обучению школьников практическим приложениям математики в рамках соответствующей методической линии.
Каждый модуль реализуется в обучении студентов на базовом и повышенном уровне. Представим на рис. 1 перечень теоретических вопросов согласно выделенным модулям и уровням их усвоения.
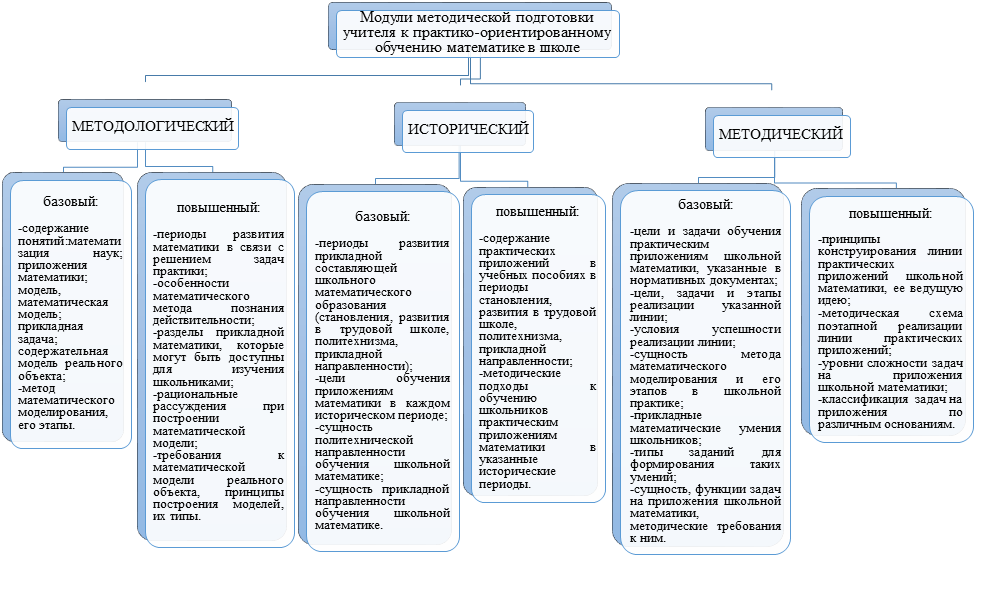
Рис.1. Двухуровневое содержание методической подготовки учителя к практико-ориентированному обучению математике в школе (теоретическое направление подготовки)
Базовый уровень предполагает овладение необходимыми минимальными методико-теоретическими знаниями в рамках данного модуля, а повышенный – расширяет и углубляет знания базового уровня, создавая возможность для их применения в исследовательском контексте. Предполагается, что при методической подготовке к практико-ориентированному обучению математике в школе в бакалавриате, студентам достаточно иметь базовый уровень знаний по данному направлению. Его расширение до повышенного происходит при написании курсовых, выпускных квалификационных работ и при посещении курсов по выбору соответствующей тематики. При продолжении обучения в магистратуре по направлению «Педагогическое образование» студенты, в дополнение к базовому, овладевают содержанием предложенных модулей на повышенном уровне.
Методический компонент включает создание студентами собственных образовательных продуктов. В контексте данного исследования под образовательным продуктом (ОП) понимаем, с одной стороны, результат учебной деятельности студента, а с другой – компонент содержания методической подготовки будущего учителя к практико-ориентированному обучению математике в школе. Нами выделены ОП следующих типов: отдельные задачи и наборы задач, связанные с практическими приложениями математики; прикладные исследовательские и проектные задания; методические разработки элективных курсов и курсов по выбору прикладного содержания.
Характеризуя ОП «Наборы задач на приложения математики», мы уточнили понятия цепочек и циклов задач с учетом использования их в практико-ориентированном обучении. Под цепочками задач на приложения математики понимаем последовательность взаимосвязанных (по фабуле, методам решения, назначению в обучении) задач. Нами выделены три типа цепочек таких задач: 1) задачи, формирующие одно математическое понятие и имеющие сюжеты по одному тематическому направлению; 2) задачи, имеющие различные сюжеты и формирующие одно математическое понятие; 3) задачи, формирующие различные математические понятия и имеющие сюжеты по одному тематическому направлению.
Также нами предложены два методических приема для составления циклов задач на приложения математики: «От теории к ее практическим применениям» и «От практической проблемы к поиску теории для ее разрешения». Они основаны на нашем понимании цикла таких задач. Это такой набор задач, который состоит из учебной математической задачи (центральная задача цикла) со взаимосвязанными с ней задачами на приложения (задачи из «букета окрестностей») или из задачи на приложения (центральная задача цикла) со взаимосвязанными с ней учебными математическими задачами (задачи из «букета окрестностей»).
Для обучения студентов созданию остальных образовательных продуктов нами выделены их методические особенности и созданы карты разработки ОП, которые содержат примерную последовательность учебных действий обучаемых.
Целевой компонент представлен двумя категориями специальных компетенций (СК) студентов, формируемых при методической подготовке к практико-ориентированному обучению математике, – когнитивными и контекстными. Эти компетенции являются системообразующими связями построенной методической системы и конкретизируют общекультурные и профессиональные компетенции, сформулированные во ФГОС ВПО. Специальные когнитивные компетенции связаны с теоретическим направлением подготовки учителя к практико-ориентированному обучению математике в школе, а специальные контекстные компетенции отражают подготовку учителя к созданию образовательных продуктов для осуществления такого обучения. Их перечень представлен в табл. 1.
Таблица 1
Специальные компетенции студентов, формируемые при методической подготовке к практико-ориентированному обучению математике
|
СПЕЦИАЛЬНЫЕ КОМПЕТЕНЦИИ |
|
|
КОГНИТИВНЫЕ |
КОНТЕКСТНЫЕ |
|
СК-1. Способен использовать знания об особенностях прикладной математики для организации прикладной математической деятельности учащихся. Владеет понятиями «математизация наук», «математическая модель», «метод математического моделирования» для обучения школьников практическим приложениям математики. СК-2. Готов к использованию исторического опыта обучения приложениям математики в современном образовательном процессе; готов актуализировать его в необходимых ситуациях интеллектуально-познавательной деятельности школьников. СК-3. Способен отбирать и адаптировать учебный материал в соответствии с целями и задачами практико-ориентированного обучения математике в школе. |
СК-4. Способен составлять задачи и наборы задач на приложения базового и повышенного уровня трудности, предназначенные для поэтапной реализации линии практических приложений математики на основной и старшей ступени общего образования. Владеет методикой обучения школьников решению задач на приложения методом математического моделирования. СК-5. Готов проводить внеклассные занятия (курсы по выбору, элективные курсы) по математике, направленные на изучение дополнительных разделов школьного курса математики, связанных с ее практическими приложениями. СК-6. Способен руководить прикладной исследовательской и проектной деятельностью школьников по математике. |
Эти компетенции имеют тесную связь с другими компонентами системы. Специальные когнитивные компетенции СК-1 – СК-3 определили модули содержательного компонента системы. Так, компетенция СК-1 обусловила содержание методологического модуля, СК-2 – исторического, а СК-3 – методического. Специальные контекстные компетенции СК-4 – СК-6 определили типы образовательных продуктов в методическом компоненте системы. В частности, компетенция СК-4 обусловила выделение ОП «Наборы задач, связанные с практическими приложениями математики», СК-5 – ОП «Элективные курсы и курсы по выбору прикладного содержания», а СК-6 – ОП «Прикладные исследовательские и проектные задания».
В свою очередь, модули содержательного компонента системы задают теоретическое направление оценивания, а образовательные продукты методического компонента непосредственно связаны с критериями и показателями их оценивания (практическое направление) в результативно-оценочном компоненте.
По этим двум направлениям (теоретическому и практическому) разработаны методические материалы для оценивания подготовки студентов к практико-ориентированному обучению математике в школе. По первому направлению итоговая проверка усвоения теоретического содержания модулей осуществляется с помощью теста, объединяющего три блока заданий: методологический, исторический и методический. По второму, практическому направлению итоговая проверка результативности подготовки студентов производится путем оценивания качества создаваемых студентами ОП согласно разработанным нами критериям: 1.Математическое содержание продукта. 2. Соответствие содержания продукта поставленной методической задаче. 3. Опора на соответствующее содержание обучения математике в школе, знание имеющейся методической литературы, нормативных документов. 4. Адекватность выбранных методов и технологий обучения поставленным целям и содержанию продукта. 5. Возможность реализации продукта на базовом и продвинутом уровне обучения. 6. Соответствие методическим требованиям к данному виду продукта. 7. Возможность достижения заданных образовательных результатов.
Для текущего контроля практической подготовки студентов разработаны подготовительные задания к созданию ОП. Они разделены на две группы: индивидуальные задания к практическим занятиям и задания для самостоятельной работы студентов. Индивидуальные задания представлены по четырем направлениям: 1. Задачи на приложения математики. Классификация, функции, уровни сложности, методические требования. 2. Метод математического моделирования в обучении математике в школе. 3. Задачи на приложения на уроках математики. 4. Обучение практическим приложениям математики во внеурочное время. Характерной особенностью индивидуальных заданий для студентов является наличие в них вариативных компонентов, которые позволяют преподавателю индивидуализировать предлагаемые задания, охватить большее число рассматриваемых вопросов. К вариативным компонентам таких заданий относим: классы, ступени, профили обучения общего образования; классификационные признаки, функции, уровни сложности задач на приложения; этапы метода математического моделирования; темы, понятия и т.п. школьного курса математики; виды внеклассной работы по математике. Задания для самостоятельной работы студентов носят «накопительный» характер и также имеют четыре направления: 1. Составление методического «паспорта» задачи на приложения. 2. Создание методической «копилки» задач на приложения. 3. Анализ практических приложений математики в учебных пособиях для школьников. 4. Составление задач на приложения (по предоставленным информационным материалам или путем подбора фабулы к учебной задаче).
Представим установленные связи между компонентами методической системы учителя к практико-ориентированному обучению математике в школе в виде графической модели (рис. 2).
Представленная модель – лишь небольшой шаг в решении проблемы определения требований и соответствующих им критериев и показателей оценивания профессиональной деятельности педагога. Сформулированные нами специальные компетенции подготовки учителя предназначены для установления результатов обучения студентов педвузов при реализации соответствующих ФГОС ВПО. Однако эти компетенции и соответствующие им оценочные средства и методы, по нашему мнению, могут быть использованы для установления уровня квалификации педагога. В реальных условиях оценки профессиональной деятельности конкретного учителя математики целесообразно усилить практическое направление оценивания, соотнеся его с образовательными результатами школьников, обучавшимися у этого учителя.
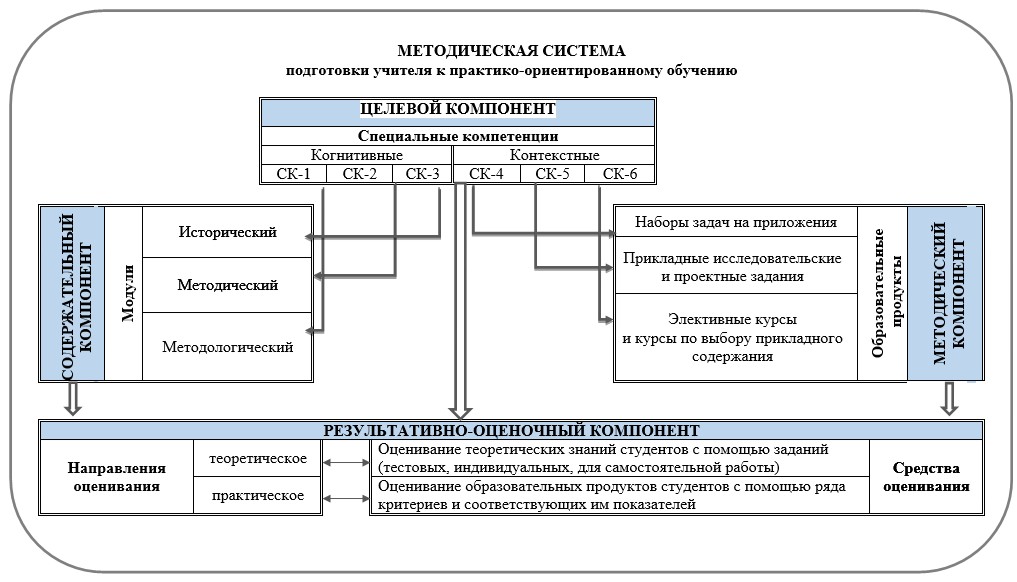
Рис. 2. Модель методической системы подготовки учителя к практико-ориентированному обучению математике в школе
Рецензенты:
Гусев В.А., д,п.н., профессор кафедры элементарной математики и методики обучения математике МПГУ, г. Москва.
Кучугурова Н.Д., д.п.н., профессор кафедры элементарной математики и методики обучения математике МПГУ, г. Москва.
Библиографическая ссылка
Егупова М.В. МОДЕЛЬ МЕТОДИЧЕСКОЙ СИСТЕМЫ ПОДГОТОВКИ УЧИТЕЛЯ К ПРАКТИКО-ОРИЕНТИРОВАННОМУ ОБУЧЕНИЮ МАТЕМАТИКЕ В ШКОЛЕ // Современные проблемы науки и образования. 2014. № 3. ;URL: https://science-education.ru/ru/article/view?id=13619 (дата обращения: 11.02.2026).



