Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Филипенко Н.М. 1 Михальчук А.А. 1 Арефьев В.П. 1

---

1 ФГБОУ ВПО «Национальный исследовательский Томский политехнический университет»

Проведен дисперсионный анализ результатов динамического оценивания знаний по высшей математике студентов очной формы обучения Томского политехнического университета. Рассмотрение проведено в системе 4-х показателей: ВК – результаты входного контроля, АТТ – результаты текущей аттестации, ЭКЗ – результат классического экзамена, ЭКЗ – скорректированные результаты ЭКЗ. Сделан вывод о высоко значимой динамике успеваемости по совокупности показателей. В рамках параметрического дисперсионного анализа с повторными измерениями оценена также составная тернарная (ДОЛГ, УДОВЛ, КАЧ) динамика успеваемости: текущая {ВК, АТТ} характеризуется высоко значимым уровнем по всем трем компонентам; после экзаменационная {ЭКЗ, ЭКЗ} – высоко значимым уровнем по двум компонентам ДОЛГ, УДОВЛ и незначимым уровнем по КАЧ; экзаменационная {АТТ, ЭКЗ} – сильно значимым уровнем по ДОЛГ, статистически значимым по УДОВ при незначимом по КАЧ. Сделан вывод о высоко значимой неоднородности результатов каждого показателя ВК, АТТ, ЭКЗ, ЭКЗ по совокупности групп на основании F-критерия дисперсионного анализа для независимых выборок. Непараметрические альтернативы однофакторного дисперсионного анализа для независимых выборок (критерий Краскела-Уоллиса и медианный тест) подтверждают эти выводы. В случае ВК для каждой тернарной переменной F-критерий оценивает уровень значимости различия между 3-мя групповыми кластерами: высоко значимо по ВКд, сильно значимо по ВКк и статистически значимо по ВКу. Результаты проведенного статистического анализа могут быть учтены в рамках проходящей реформы высшего образования.

Статья в формате PDF

347 KB

контроль успеваемости студентов

дисперсионный анализ

1. Акерман Е.Н., Михальчук А.А., Трифонов А.Ю. Кластеризация социально-экономических вузов на основе рейтингов вступительных испытаний // Вестник Томского государственного университета. – 2013. – № 367. – С. 100-104.

2. Арефьев В.П. , Михальчук А.А. , Филипенко Н.М. Сравнительный статистический анализ входного и текущего контроля математических знаний в рамках классической формы заочного высшего образования // Современные проблемы науки и образования. – 2013. – №. 5. (Электронный журнал); URL:www.science-education.ru/111-10676 (дата обращения: 22.02.2014).

3. Арефьев В.П., Михальчук А.А., Филипенко Н.М. Тернарная кластеризация показателей образовательной деятельности студентов вузов // Современные проблемы науки и образования. – 2014. – № 3; URL: http://www.science-education.ru/117-13211 (дата обращения: 23.05.2014).

4. Багаутдинова С.Ф., Левшина Н.И., Санникова Л.Н., Турченко В.И. Разработка и организация системы мониторинга качества образовательной деятельности студентов в высшем учебном заведении // Фундаментальные исследования. – 2014. – № 1-0. – С. 109-114.

5. Жичкин А.М. Метод применения инструментария контроля качества в организациях высшего профессионального образования // Высшее образование сегодня. – 2014. – № 1. – С. 19-25.

6. Куликова О.В., Поповский Э.Е., Филиппова Е.Г. Выявление динамики математической подготовки студентов вуза по статистическим данным педагогических измерений // Современные проблемы науки и образования. – 2013. – № 1; URL: www.science-education.ru/107-8568 (дата обращения: 22.02.2014)

7. Сенашенко В.С., Ткач Г.Ф. Системы оценки академических достижений учащихся как инструмент управления и контроля // Высшее образование в России – 2013. – № 10. – С. 3-13.

8. Сидорова С.Н. Проблема оценивания компетенций у студентов в контексте введения ФГОС ВПО третьего поколения // Инновации в образовании. – 2013. – № 09. – С. 67-72.

9. Трубилин А.И., Григораш О.В. Оценка качества подготовки студентов и эффективности учебной работы преподавателей // Высшее образование сегодня. – 2014. – № 3. – С. 7-10.

10. Халафян А.А. STATISTICA 6. Статистический анализ данных. Учебник – М: ООО «Бином-Пресс», 2008 г. – 512 с.

Модернизация высшей школы в современных условиях ставит своей целью решение проблем повышения качества образования и оценивания качества обучения [4–9]. Согласно федеральным государственным образовательным стандартам высшего профессионального образования (ФГОС ВПО), приоритетной задачей управления качеством образования выступает оценка качества освоения основных образовательных программ, включающая предварительную, текущую и итоговую формы контроля результатов образовательной деятельности студентов, в рамках рейтинговой системы оценок с дальнейшим переводом их в экзаменационную (зачетную) оценку. Контроль качества образования приобретает характер непрерывного контроля результатов образовательного процесса и предполагает проведение измерения показателей образовательной деятельности студентов в соответствии с ФГОС ВПО. В нашем случае это измерение (оценивание) результатов образовательной деятельности студентов: ВК – результаты входного тестирования по математике в начале текущего семестра, АТТ. – результаты аттестации по математике в конце текущего семестра, ЭКЗ. – результат классического экзамена в конце текущего семестра, ЭКЗ.* – скорректированные результаты ЭКЗ. в середине следующего семестра.

В данной работе (аналогично [2] в системе заочного обучения) проведен в пакете Statistica [10] статистический анализ результатов динамического оценивания знаний по высшей математике (выборка 25-и учебных групп объема n =503) в рамках 1-го семестра студентов очной формы обучения Томского политехнического университета (ТПУ1).

Динамика успеваемости ТПУ1 на уровне средних в переменных {ВК, АТТ., ЭКЗ., ЭКЗ.*} приведена на рис. 1, а соответствующая более детальная составная тернарная динамика – на рис. 2.

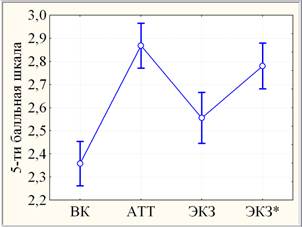
Рис. 1. Динамика успеваемости ТПУ1 на уровне средних

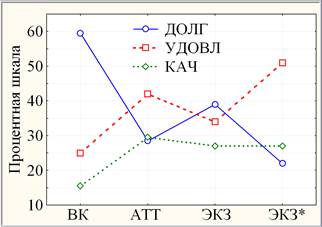
Рис. 2. Составная тернарная динамика успеваемости ТПУ1

Для оценки значимости динамики успеваемости применен параметрический дисперсионный анализ повторных измерений. Параметрический F-критерий для зависимых выборок приводит к выводу о высоко значимой (р< 0,0005) динамике успеваемости ТПУ1 по совокупности показателей {ВК, АТТ., ЭКЗ., ЭКЗ.*}. Применение непараметрического (рангового) дисперсионного анализа Фридмана с повторными измерениями подтвердило результаты параметрического дисперсионного анализа повторных измерений.

В рамках параметрического дисперсионного анализа на основании критериев множественного сравнения на уровне средних (рис. 1) сделан вывод о незначимом различии (уровень значимости р> 0,10) между АТТ. (mАТТ≈ 2,87) и ЭКЗ.* (mЭКЗ*≈ 2,78). При этом различие между ВК (mВК≈ 2,36) и ЭКЗ. (mЭКЗ≈ 2,56), а также между ЭКЗ. и ЭКЗ.* оценивается как высоко значимое (р< 0,0005). Полученные результаты подтверждаются ранговым критерием Вилкоксона для зависимых выборок.

Применение F-критерия дисперсионного анализа для независимых выборок приводит к выводу о высоко значимой неоднородности (на уровне значимости р< 0,0005) результатов каждой формы контроля результатов образовательной деятельности студентов ВК., АТТ., ЭКЗ., ЭКЗ.* по совокупности групп. Заметим, что непараметрические альтернативы однофакторного дисперсионного анализа для независимых выборок (критерий Краскела – Уоллиса и медианный тест) подтверждают эти выводы.

Соответствующая рисунку 1 более детальная составная тернарная динамика успеваемости ТПУ1 приведена на рис. 2 в рамках тернарного подхода [1, 3] в системе 3-х показателей формы контроля результатов образовательной деятельности студентов по 5-ти балльной шкале: ДОЛГ – доля сдавших на «неуд.» (в диапазоне [0; 2,5) по 5-ти балльной шкале) и не допущенных, УДОВЛ. – доля сдавших на «удовл.» (в диапазоне [2,5; 3,5)) и КАЧ. – доля сдавших на «хор. + отл.» (в диапазоне [3,5; 5]). При этом ДОЛГ + УДОВЛ. + КАЧ. = 100 % для любой учебной группы.

Согласно рис. 1–2, налицо высоко значимая (р< 0,0005) положительная текущая тернарная динамика успеваемости {ВК, АТТ.}: убывание ДОЛГ с 58 % до 28 % и рост как УДОВ. с 26 % до 42 %, так и КАЧ. с 16 % до 30 %, а также положительная динамика периода после экзаменационной ликвидации задолженностей {ЭКЗ., ЭКЗ.*}: высоко значимое (р< 0,0005) убывание ДОЛГ с 39,5 % до 23 % и высоко значимый (р< 0,0005) рост УДОВ. с 33,5 % до 50 % при стабильном уровне КАЧ. (27 %). Отрицательная динамика успеваемости экзаменационного периода {АТТ., ЭКЗ.}, проявившаяся, в сильно значимом (0,0005<р»0,004< 0,005) росте ДОЛГ. с 28 % до 39,5 % и статистически значимом (0,005<р»0,045< 0,05) убывании УДОВ. с 42 % до 33,5 % при незначимом (р> 0,10) убывании КАЧ. с 30 % до 27 %, объясняется естественной сложностью итоговой семестровой контрольнойдля слабых студентов.

Для геометрической интерпретации составной тернарной (ДОЛГ, УДОВЛ., КАЧ.) динамики в переменных {ВК, АТТ., ЭКЗ., ЭКЗ.*} успеваемости ТПУ1 (рис. 2) использована также тернарная диаграмма рассеяния в 4-х уровневой тернарной (ДОЛГ, УДОВЛ., КАЧ.) системе координат [3] (рис. 3 слева), делящей исходный треугольник на 16 равносторонних маленьких треугольников (D), в которой тернарная динамика успеваемости ТПУ1 представлена в виде последовательности 4-х точек ВК, АТТ., ЭКЗ., ЭКЗ.* на рис. 3 (справа): ВК (0,58; 0,26; 0,16) на границе DДд и DДу, АТТ(0,28; 0,42; 0,3) на границе DЦ и DЦд, ЭКЗ. (0,395; 0,335; 0,27) на границе DЦ и DЦк, ЭКЗ*(0,23; 0,5; 0,27) в общей вершине DЦ и DУк.

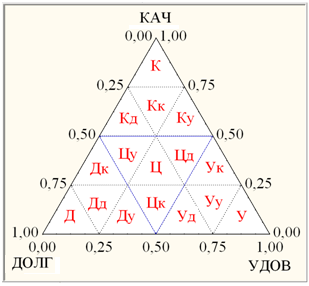
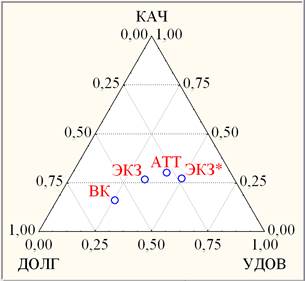
Рис. 3. Тернарная динамика успеваемости ТПУ1 (справа) в 4-х уровневой тернарной системе координат (слева)

При этом динамика успеваемости ТПУ1 по совокупности показателей {ВК, АТТ., ЭКЗ., ЭКЗ.*} оценена, как было отмечено выше, высоко значимо (р< 0,0005). Более того, соответствующим уровнем значимости оценена составная тернарная (ДОЛГ, УДОВЛ., КАЧ.) динамика успеваемости ТПУ1: текущая {ВК, АТТ} характеризуется высоко значимым уровнем (р< 0,0005) по всем трем компонентам ДОЛГ, УДОВЛ., КАЧ.; после экзаменационная {ЭКЗ., ЭКЗ.*} характеризуется высоко значимым уровнем (р< 0,0005) по двум компонентам ДОЛГ, УДОВЛ. и незначимым уровнем (р> 0,10) по КАЧ.; экзаменационная {АТТ., ЭКЗ.} характеризуется сильно значимым уровнем(0,0005<р< 0,005) по ДОЛГ, статистически значимым (0,005<р< 0,05)по УДОВ. при незначимом (р> 0,10) по КАЧ.

Положение точек ВК, АТТ., ЭКЗ., ЭКЗ.* в тернарной системе координат на рис. 3 (справа) определяется усредненными значениями (ДОЛГ, УДОВЛ., КАЧ.) по 25-и учебным группам, составляющим выборку ТПУ1. Представление о степени групповой неоднородности ТПУ1 дает контрастная групповая тернарная динамика успеваемости на примере 10-ти из 25-ти учебных групп (рис. 4).

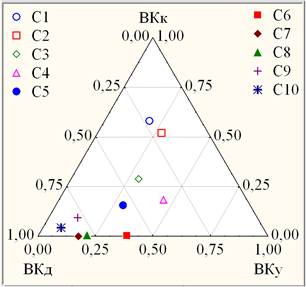
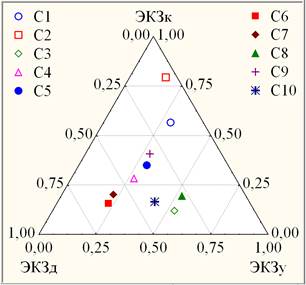
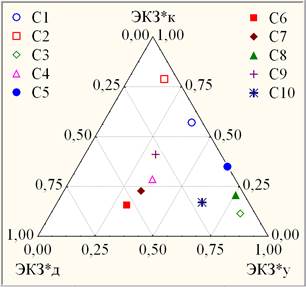
Рис. 4. Тернарная динамика успеваемости 10-ти учебных групп

С одной стороны, аналогично тернарной динамике успеваемости ТПУ1 (рис. 3 справа) можно оценить очень пеструюгрупповую тернарную динамику успеваемости (табл. 1).

Таблица 1

Групповая тернарная динамика успеваемости

С другой стороны, проведение кластеризацииучебных групп студентов в 3-х мерном пространстве {ДОЛГ, УДОВЛ. и КАЧ.} дендрограммным методом и методом K-средних [3] приводит к выводу о значимой неоднородности результатов каждой формы контроля результатов образовательной деятельности студентов ВК, АТТ., ЭКЗ., ЭКЗ.* по совокупности компонент {ДОЛГ, УДОВЛ. и КАЧ.}. Например, для ВК значению расстояния объединения, равного 0,75 (красная пунктирнаягоризонтальная прямая), соответствует разбиение 10-ти групп С1-10 на 3 кластера (С1-2, С3-6, С7-10), обладающее устойчивостью относительно вариации мер близости и правил объединения двух кластеров (рис. 5).

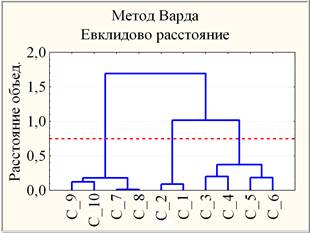
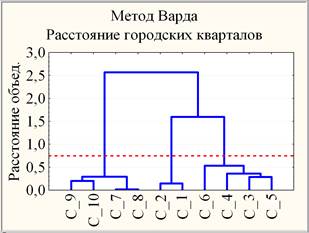
Рис. 5. Горизонтальная дендрограмма групп в пространстве {ДОЛГ, УДОВЛ. и КАЧ.} для ВК

Результаты кластеризации учебных групп студентов дендрограммным методом (рис. 5) находятся в точном соответствии с взаимным расположением групп на диаграмме рассеяния в тернарных переменных {ДОЛГ, УДОВЛ. и КАЧ.} (ВК на рис. 4).

В рассматриваемом случае ВК (рис. 4–5) F-критерий показывает, что для каждой тернарной переменной (ВКд, ВКу, ВКк) различие между 3-мя кластерамизначимо: высоко значимо (p»0,0002 < 0,0005) по ВКд, сильно значимо (0,0005<p»0,0007 < 0,005) по ВКк и статистически значимо (0,005<p»0,008 < 0,05) по ВКу.

Выводы

1. Параметрический F-критерий для зависимых выборок приводит к выводу о высоко значимой (р< 0,0005) динамике успеваемости ТПУ1 по совокупности показателей {ВК, АТТ., ЭКЗ., ЭКЗ.*}. На основании критериев множественного сравнения на уровне средних сделан вывод о незначимом различии (уровень значимости р> 0,10) между АТТ. (mАТТ≈ 2,87) и ЭКЗ.* (mЭКЗ*≈ 2,78). При этом различие между ВК (mВК≈ 2,36) и ЭКЗ. (mЭКЗ≈ 2,56), а такжемежду ЭКЗ. и ЭКЗ.* оценивается как высоко значимое (р< 0,0005). Применение непараметрического (рангового) дисперсионного анализа Фридмана с повторными измерениями подтвердило этот результат.
2. В рамках параметрического дисперсионного анализа с повторными измерениями соответствующим уровнем значимости оценена составная тернарная (ДОЛГ, УДОВЛ., КАЧ.) динамика успеваемости ТПУ1: текущая {ВК, АТТ.} характеризуется высоко значимым уровнем (р< 0,0005) по всем трем компонентам ДОЛГ, УДОВЛ., КАЧ.; после экзаменационная {ЭКЗ, ЭКЗ*} – высоко значимым уровнем (р< 0,0005) по двум компонентам ДОЛГ, УДОВЛ. и незначимым уровнем (р> 0,10) по КАЧ.; экзаменационная {АТТ., ЭКЗ.} – сильно значимым уровнем (0,0005<р< 0,005) по ДОЛГ, статистически значимым (0,005<р< 0,05) по УДОВ при незначимом (р> 0,10) по КАЧ.
3. Сделан вывод о высоко значимой неоднородности (на уровне значимости р< 0,0005) результатов каждой формы контроля результатов образовательной деятельности студентов ВК, АТТ., ЭКЗ., ЭКЗ.* по совокупности групп на основании F-критерия дисперсионного анализа для независимых выборок. Непараметрические альтернативы однофакторного дисперсионного анализа для независимых выборок (критерий Краскела – Уоллиса и медианный тест) подтверждают эти выводы.
4. В случае ВК для каждой тернарной переменной (ВКд, ВКу, ВКк) F-критерий оценивает уровень значимости различия между 3-мя кластерами: высоко значимо (p»0,0002 < 0,0005) по ВКд, сильно значимо (0,0005<p»0,0007 < 0,005) по ВКк и статистически значимо (0,005<p»0,008 < 0,05) по ВКу.
5. Результаты тернарной динамики показывают роль организации образовательного процесса и могут быть учтены в оценке качества образования и контроля знаний.

Работа выполнена при поддержке Российского научного фонда.

Рецензенты:

Трифонов А.Ю., д.ф.-м.н., профессор кафедры высшей математики и математической физики, ФГБОУ ВПО «Национальный исследовательский Томский политехнический университет, г. Томск.

Арефьев К.П,, д.ф.-м.н., профессор кафедры высшей математики, ФГБОУ ВПО «Национальный исследовательский Томский политехнический университет, г. Томск.

Библиографическая ссылка