Технологический процесс резания поверхностей в условиях неопределенности по их ориентации в части малых перемещений накладывает определенные требования на системы управления, обусловленные габаритами и видом поверхностей объекта резания, пространственными ограничениями от внешних объектов, точностью движения по технологической поверхности и необходимостью стабилизации расстояния режущей кромки головки инструмента от технологической поверхности. Характерной особенностью объектов управления здесь является возникающее при изменении управляющего или возмущающего воздействия геометрически-силовое взаимовлияние координатных приводов. Это, также, имеет место в процессах сборки, сварки и гидрорезания, когда технологическая поверхность в пространстве не совпадает с расчетной. Цель управления технологическим роботом, в данном случае, состоит в обеспечении технологического процесса, а также при необходимости адаптации программной траектории к фактической с обеспечением требуемого вектора усилия при внешних флуктуирующих возмущениях. При этом, следует парировать внешние межкоординатные возмущения, обусловленные динамическими нагрузками со стороны объекта или выполняемого технологического процесса, или возникающими при отклонении координат расположения рабочей поверхности в процессах сварки и гидрорезания.
Широкое распространение для систем автоматического управления (САУ) отмеченного типа получило управление, основанное на положениях теории инвариантности. По сравнению с другими методами коррекции введение инвариантных входов повышает точность, не изменяя свойств замкнутого контура системы. Универсальной является вторая форма инвариантности, однако она требует получения n производных, где n – порядок системы, что при их числе более двух трудно реализуется. Большими возможностями для обозначенного класса технологических процессов и систем управления обладает модифицированная четвертая форма инвариантности [2,3].
Рассмотрим этот вопрос в следующей постановке. Имеется система с номинальными управлением g0(p) и возмущением на выходе f0(p). Последнее обусловлено создаваемым на выходе силовым воздействием при выполнении технологического процесса. По различным технологическим факторам имеется отклонение фактического усилия от расчетного на величину Δf(p). Необходимо ошибку, обусловленную составляющей Δf(p), скомпенсировать дополнительным управлением Δg(p). Иначе, имеем функции управления и возмущения в виде
![]()
![]()
Для компенсации дополнительного возмущения условие четвертой формы инвариантности здесь запишется
![]()
Классическая трактовка четвертой формы инвариантности предусматривает введение дополнительной составляющей в управлении для каждого канала по своему воздействию: для управляющего воздействия - в функции воздействия g(p), для возмущающего воздействия - в функции возмущающего воздействия f(p). В нашем же случае, для парирования возмущения f(p) вводится дополнительная составляющая в управляющее воздействие в виде Δg(p). Выполнение условий модифицированной четвертой формы инвариантности для компенсации Δf(p) возможно в следующих вариантах: 1) формированием дополнительного полинома В2(р) при выбранном Δg(p); 2) формированием дополнительного управления Δg(p) при выбранном В2(р); 3) выбором произведения В2(р)Δg(p). С позиции технической реализации целесообразно вводить дополнительное управление, которое при выбранной функции В2(р) определяется из условия
![]()
Для физической реализации формирования Δg необходимо выделить составляющую ошибки, пропорциональную Df. Для этого можно использовать информацию с силомоментных датчиков или обработкой сигнала тока исполнительного двигателя. При их отсутствии составляющую ΔDf можно получить обработкой суммарной ошибки в контуре системы, исключив из суммарной ошибки другие, в данном случае детерминированные составляющие, которые могут быть получены, например, с помощью эталонной модели.
Реализация модифицированной четвертой формы инвариантности возможна с использованием методов самонастройки, один из которых предусматривает формирование дополнительной составляющей в уже сформированное управляющее воздействие. Данный метод адаптации рассмотрен на примере двух структур, представленных на рис. 1. На схемах обозначены: W1(p) – передаточная функция привода с кинематической передачей и объектом управления; V(p) – передаточная функция привода по возмущению; K(p) – передаточная функция звена адаптации управляющего сигнала; g0, f – управляющее и возмущающее воздействия привода соответственно; X, X0 – непосредственно регулируемая координата и приведенная координата смежного привода соответственно; δ – суммарная ошибка системы; Δf – отклонение фактического усилия от расчетного; δf0 – составляющая ошибки системы, обусловленная возмущающим воздействием; δΔf – моментная составляющая ошибки; Δg – дополнительная составляющая управляющего воздействия.
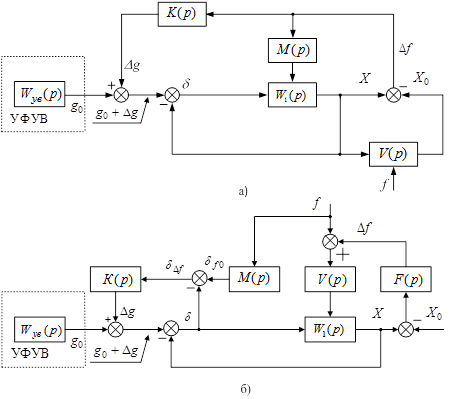
Рис.1. Структурные схемы САУ с формированием дополнительного управления
Согласно структурной схеме, представленной на рис. 1,а, дополнительная составляющая управления формируется на основе разности координат приводов, определяющей их геометрически-силовое взаимовлияние или обусловленной несовпадением программной и фактической траекторий. На рис.1.а блок с передаточной функцией V(p) представляет симулятор другой координаты, участвующей в формировании технологической программной траектории. Для синхронизации их взаимодействия введена связь с выхода первого привода. Второй способ, иллюстрируемый структурной схемой на рис. 1,б, предусматривает формирование дополнительной составляющей, как функции моментой ошибки от нерасчетного возмущения или от разности программной и фактической траекторий. В контур адаптации вводятся интегрирующие звенья со степенью интегрирования, пропорциональной степени производной управляющего воздействия.
В зависимости от вида управляющего воздействия, возмущения со стороны внешней среды (приводов последующих координат в системах с последовательной кинематикой, например, в промышленных роботах с угловой системой координат), формируемого в данных схемах симулятором смежной координаты, проанализируем взаимосвязь воздействий, ошибок и необходимой коррекции.
Случай 1. Управляющее воздействие имеет вид:
![]()
При этом, скорости задающего сигнала исследуемого привода и привода последующей координаты, формируемой здесь симулятором, совпадают, т.е.
![]()
где: V, V0 – скорость выполняемого технологического процесса по первой координате и скорость привода второй координаты, формируемой симулятором, соответственно. Геометрически-силовое взаимовлияние приводов обусловлено разностью координат приводов, т.е.
![]()
где: X0 – координата смежного привода.
В данном случае, звено K(p), реализующее необходимую коррекцию управляющего сигнала, должно иметь передаточную функцию:
![]()
где α*0 – коэффициент передачи в канале формирования дополнительного управления.
Случай 2. Управляющее воздействие имеет вид:
![]()
![]()
При этом, ошибка положения обусловлена разностью скоростей приводов первой и второй координат, формируемой симулятором, т.е.
![]()
Тогда, звено K(p) должно иметь передаточную функцию:
![]()
где: α*1 – коэффициент передачи в канале формирования дополнительного управления.
Случай 3. Управляющее воздействие имеет вид:
![]()
![]()
где: ε – ускорение исследуемого привода. При этом, ошибка положения обусловлена разностью ускорений задающего сигнала первого и последующего приводов, т.е.
![]()
где: ε0 – ускорение смежного привода.
Тогда, звено K(p) должно иметь передаточную функцию:
![]()
где: α*2 – коэффициент передачи в канале формирования дополнительного управления.
Моделирование структур (рис.1) с каналом адаптации сигнала задания по положению, скорости и ускорению было реализовано в среде пакета программы MatLab – Simulink. В частности, проводился анализ точности системы управления в режиме движения с постоянной скоростью и при отработке гармонического входного сигнала. В роли объекта исследования выступает привод перемещения с главной обратной связью по положению исполнительного механизма. Привод включает в себя два внутренних контура: по напряжению и частоте вращения двигателя и ПИД регулятор. Главное возмущающее воздействие, обусловлено геометрически-силовым взаимовлиянием координатных приводов и отклонением фактической траектории исполнительного органа от заданной. В качестве привода смежной координаты выступает симулятор межкоординатных возмущений. В зависимости от вида сигнала задания его выходная координата описывается уравнениями:
Случай 1. Канал адаптации по положению
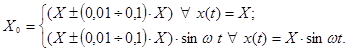
Случай 2. Канал адаптации по скорости
![]()
Случай 3. Канал адаптации по ускорению
![]()
Исследования проводились в режиме изменения момента нагрузки Mн(t), обусловленного влиянием «другой» координаты, в интервале от 1 до 5 Нм (при номинальном моменте привода 2 Нм). В ходе моделирования плавно изменялась скорость задания управляющего воздействия в диапазоне 10…80 мм/с для каналов адаптации по положению и скорости, а также ускорение входного сигнала в пределах от 1 до 20 мм/с2 для канала адаптации по ускорению. Соотношение координат приводов (в части отклонения фактической и расчетной траекторий) варьировалось от 1 до 10%. Исследуемый привод в режиме движения с постоянной скоростью имеет ошибку положения, обусловленную влиянием симулятора смежной координаты и изменяющуюся в пределах от 5 до 10%. Результаты моделирования САУ в режиме отработки гармонического входного сигнала показали, что вследствие внешних межкоординатных возмущений на выходе системы управления наблюдается установившаяся динамическая ошибка (10% от амплитуды задающего сигнала). Данные показатели не отвечают требованиям, предъявляемым к системам управления отмеченного типа. Введение контура адаптации позволяет свести к минимуму влияние внешних возмущений при выполнении технологического процесса по заранее заданной траектории. На рис. 2 представлены графики изменения выходной координаты привода с контуром адаптации и без него, в режиме движения с постоянной скоростью и при отработке САУ гармонического входного сигнала. На рис. 2 цифрами обозначены: 1 – график изменения выходной координаты САУ без контура адаптации; 2 – график изменения выходной координаты САУ с контуром адаптации; 3 – отклонение положения инструмента Δx от заданной траектории. Рис. 3 демонстрирует графики изменения показателей САУ в течение времени процесса компенсации.
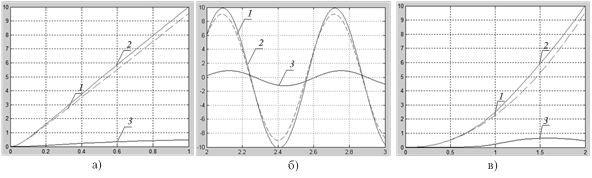
Рис.2. Исследование показателей точности системы управления:
а) графики изменения выходной координаты САУ в режиме движения с постоянной скоростью, для каналов адаптации по скорости и положению (V=10 мм/с, Δx=5%, Mн = 5 Нм); б) графики изменения выходной координаты САУ при отработки гармонического входного сигнала для канала адаптации по положению (А=10, ω=10 рад/с, Mн = 5 Нм); в) графики изменения выходной координаты САУ для канала адаптации сигнала задания по ускорению (ε=5 мм/с2, ε / ε0 =10% , Mн = 5 Нм)
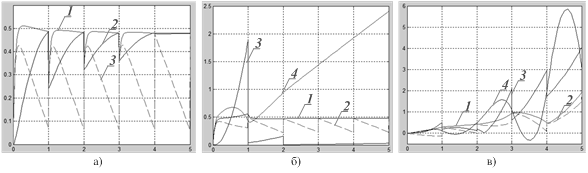
Рис. 3:
1 – график изменения ошибки системы управления δ; 2 – график моментной составляющей ошибки δΔf график отклонения фактического усилия от расчетного Δf; 3 – график изменения дополнительной составляющей управления Δg; 4 – график отклонения фактического усилия от расчетного Δf
В ходе моделирования получены зависимости коэффициента передачи звена K(p) в канале адаптации от скорости (частоты) задающего воздействия для контура адаптации по скорости и положению, а также от ускорения сигнала задания для контура адаптации по ускорению (рис. 4).
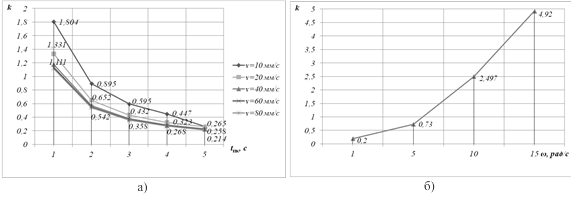
Рис. 4. Графики изменения коэффициента передачи в канале формирования дополнительного управления для канала адаптации по положению
Выводы
-
В системах с взаимосвязью управляющего и возмущающего воздействий возможно обеспечение четвертой формы инвариантности за счет адаптации уровней управляющего воздействия (координаты и ее производных).
-
Систему управления следует рассматривать в виде последовательно соединения двух подсистем - устройства формирования управляющего воздействия и непосредственно системы координатных приводов.
-
Исследуемый способ реализации контура адаптации, предусматривает формирование автономных составляющих, суммируемых с сигналов соответствующей производной, что ведет к повышению степени астатизма эквивалентной передаточной функции системы на единицу относительно астатизма управляющего воздействия.
-
Результаты проведенных исследований подтверждают работоспособность рассмотренных алгоритмов. Необходимо введение звена с переменным коэффициентом передачи в каналах адаптации.
Рецензенты:
Гоц А.Н., д.т.н., профессор кафедры «Тепловые двигатели и энергетические установки», ФГБОУ ВПО «Владимирский государственный университет имени Александра Григорьевича и Николая Григорьевича Столетовых», г. Владимир.
Кульчицкий А.Р., д.т.н., доцент, главный специалист ООО «Завод инновационных продуктов «Концерн тракторные заводы»», г. Владимир.
Библиографическая ссылка
Кобзев А.А., Новикова Н.А., Лекарева А.В., Махфуз А.А. ИССЛЕДОВАНИЕ АЛГОРИТМОВ ДИНАМИЧЕСКОЙ КОРРЕКЦИИ ДВИЖЕНИЯ В РОБОТОТЕХНИЧЕСКИХ СИСТЕМАХ // Современные проблемы науки и образования. 2014. № 3. ;URL: https://science-education.ru/ru/article/view?id=13573 (дата обращения: 11.02.2026).



