Введение
Климатические условия различных регионов России характеризуются непостоянством, резкими перепадами температур воздуха, устойчивой повышенной влажностью и скоростью ветра, частой сменяемостью в течение рабочего дня. Всвязи с чем возрастает роль одежды, обладающей улучшенными эксплуатационными и защитными свойствами; одежды, предназначенной для поддержания длительного теплового равновесия между организмом человека и окружающей средой.
Появление текстильных материалов с новыми свойствами и развитие компьютерных технологий существенно изменили традиционные подходы к процессам проектирования и производства теплозащитной одежды. Ранее было рассчитано регрессионное уравнение взаимосвязи теплоизоляции комплекта со средневзвешенной толщиной пакета материалов [5], а также уравнение линейной множественной регрессии [4] взаимосвязи суммарного теплового сопротивления покровных материалов с поверхностной плотностью и воздухопроницаемостью. Были проведены исследования по установлению влияния вредных производственных и климатических факторов на организм человека [2], произведен ориентировочный расчет необходимой теплоизоляции защитной одежды, время допустимого непрерывного пребывания на холоде на примере нефтедобывающего производства южного климатического региона России [1].
1.Факторный анализ показателей свойств покровных материалов
На теплоизоляцию одежды оказывают влияние теплофизические (тепловое сопротивление, теплопроводность, теплоемкость) и структурные (пористость, средняя плотность, толщина) показатели свойств материалов, применяемых в комплекте теплозащитной одежды [3]. Задачей нашего исследования было изучение взаимосвязей между показателями предоставленной выборки многомерного случайного вектора, представляющего собой теплофизические параметры покровных материалов многофункциональной структуры теплозащитной одежды (таблица 1). Наше исследование было необходимо для обоснованных рекомендаций теоретических подходов к разработке проектирования и моделирования теплоизоляционных компонентов защитной одежды для швейной отрасли.
В работе исследовали девять показателей. Первый показатель U – суммарное тепловое сопротивление являлся искомой функцией отклика от остальных показателей: Х1 –поверхностная плотность, Х2 – воздухопроницаемость, Х3 – паропроницаемость, Х4 – гигроскопичность, Х5 – поверхностное заполнение, Х6 – общая пористость, Х7 – толщина, Х8 – влагоотдача. Указанные аргументы взаимозависимы. Например, от толщины зависят: поверхностная плотность, поверхностное заполнение, общая пористость, гигроскопичность, влагоотдача.
Таблица 1 – Экспериментальные данные измерений теплофизических параметров многофункциональной структуры теплозащитной одежды для нефтяников
|
Артикул
|
Суммарное тепловое сопротив- ление Rсум , м2 0С/Вт |
Поверх-ностная плотность,
г/м2 |
Воздухо-проница-емость,
дм3/м2с |
Паропро-ницае-мость,
мг/см2 r
|
Гигроско-пичность,
% |
Поверх-ностное заполне ние Еs, % |
Общая порис-тость,
% |
Толщина,
мм |
Влаго-отдача,
% |
|
|
Без учета ветра |
Ветер 5 м/с |
|||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
81424 |
0,542 |
0,668 |
199 |
32 |
10,5 |
5,8 |
6,926 |
92,6 |
0,51 |
76,9 |
|
81421 |
0,593 |
0,675 |
255 |
19 |
10,2 |
5,4 |
8,469 |
88,3 |
0,63 |
69,8 |
|
10408 |
0,621 |
0,630 |
304 |
21 |
10,0 |
11,7 |
8,937 |
85,4 |
0,73 |
36,9 |
|
10409 |
0,579 |
0,673 |
350 |
21 |
10,3 |
11,3 |
9,636 |
79,7 |
0,88 |
36,8 |
|
81423 |
0,482 |
0,667 |
217 |
35 |
9,7 |
5,4 |
7,458 |
92,9 |
0,45 |
73,7 |
|
18439 ax |
0,464 |
0,641 |
239 |
47 |
11,0 |
10,9 |
8,023 |
90,4 |
0,59 |
51,2 |
|
87309 |
0,599 |
0,631 |
244 |
17 |
10,6 |
5,8 |
7,575 |
91,5 |
0,47 |
68,4 |
|
16362 |
0,541 |
0,666 |
222 |
32 |
10,7 |
4,3 |
7,822 |
90,0 |
0,72 |
66,9 |
|
Климат 1 80407 |
|
|
223 |
0 |
0,9 |
1,7 |
|
|
0,31 |
89,07 |
|
Климат 2 |
|
|
236 |
0 |
6,4 |
2,3 |
|
|
0,35 |
79,4 |
|
Климат 3 |
|
|
205 |
0 |
9,8 |
1,2 |
|
|
0,32 |
78,2 |
|
80406 (без покрытия) |
|
|
173 |
40 |
11,5 |
0,9 |
|
|
0,30 |
78,1 |
Для исключения мультиколлинеарности аргументов регрессионной функции, были предварительно произведены корреляционный и факторный анализы данных средствами пакета STATISTICA ver. 8.0 (StatSoft Inc, 2009г.). На рисунке 1 представлен график собственных чисел ковариационной матрицы (дисперсия факторов).
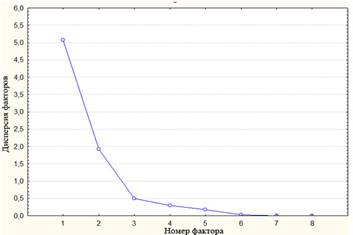
Рисунок 1 – График собственных чисел ковариационной матрицы
По критериям Кайзера и «каменистой осыпи», значимыми являются только первый и второй факторы. По матрице факторных нагрузок (таблица 2) видно, что первым фактором является толщина покровных материалов, вторым – качество покровных материалов, в данной выборке за качество отвечает воздухопроницаемость. В таблице выделены значения факторов с уровнем значимости выше 0,7.
Таблица 2 - Матрица факторных нагрузок
|
Показатели |
Фактор 1 |
Фактор 2 |
|
Поверхностная плотность |
0,957238 |
-0,184483 |
|
Воздухопроницаемость |
0,101411 |
0,891027 |
|
Паропроницаемость |
0,197119 |
0,905118 |
|
Гигроскопичность |
0,808146 |
0,349605 |
|
Поверхностное заполнение |
0,939979 |
-0,095881 |
|
Общая пористость |
-0,905969 |
0,164784 |
|
Толщина |
0,866045 |
0,305598 |
|
Влагоотдача |
-0,894290 |
-0,418875 |
Итак, аргументами регрессионной функции являются толщина и воздухопроницаемость, остальные показатели: поверхностная плотность, паропроницаемость, гигроскопичность, поверхностное заполнение, общая пористость, влагоотдача выражаются через воздухопроницаемость и толщину линейно.
2. Квадратичная регрессионная модель
Средствами пакета STATISTICA ver. 8.0 (StatSoft Inc, 2009г.) была исследована квадратичная регрессионная зависимость (рисунок 2) суммарного теплового сопротивления покровных материалов от воздухопроницаемости (Х) и толщины (Y) и получено уравнение (1):
U=0,2625+1,1451X-0,0001Y-0,741Х2-0,0054ХY-3,011*10-5Y2 (1)
Индекс корреляции полученной зависимости достаточно высок, он равен 0,98. Незначимыми являются коэффициенты: линейного члена для воздухопроницаемости (α=0,94), квадратического члена для воздухопроницаемости (α=0,57). Значимы все члены регрессии для толщины, большое значение имеет высокий уровень значимости для парного члена с толщиной и воздухопроницаемостью (α=0,33). Поэтому из модели (1) они были отброшены линейный и квадратический члены с воздухопроницаемостью и получена следующая регрессионная модель (2):
U=0,2048+1,3470X-0,8293Х2-0,0090YХ (2)
Все параметры модели значимы. Максимальный уровень значимости 0,0017. Индекс корреляции снизился незначительно до 0,979, относительная точность прогноза составляет 4% (рисунок 2, 3).
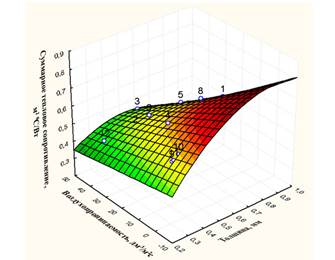
Рисунок 2 – Квадратичная регрессия зависимость суммарного теплового сопротивления от толщины и воздухопроницаемости
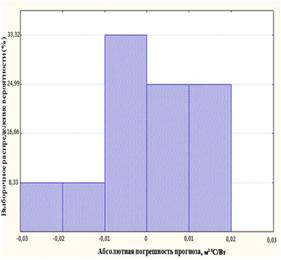
Рисунок 3 – Гистограмма остатков регрессионной модели
3. Максимальное суммарное тепловое сопротивление
Для поиска оптимального значения теплового сопротивления материала была поставлена и решена задача квадратического программирования, состоящая из целевой функции квадратической зависимости (2) и допустимого множества (3):
![]() (3),
(3),
где h – толщина материала, a – воздухопроницаемость материала.
Задача квадратического программирования была решена средствами MathCAD ver.14.0 (Parametric Technology Corporation, 2009г.). В результате чего получено оптимальное значение толщины, равное 0,8; минимально возможное значение воздухопроницаемости – 0; а прогнозируемое суммарное тепловое сопротивление – 0,75.
Благодаря проведённому анализу показателей свойств покровных материалов на примере нефтедобывающего производства южного климатического региона России, полученной регрессионной модели с расчетом максимально возможного суммарного теплового сопротивления, появилась возможность более точно выполнять расчеты толщины покровных материалов, позволяющие установить конструкцию пакета материалов одежды с максимальной теплоизоляцией, отвечающей всем современным требованиям. Так, учет принципов формирования теплоизоляции, сохранение теплового гомеостаза за счет свойств воздухопроницаемости, паропроницаемости и других, обеспечивающих «дышащие» свойства одежды, позволяет достичь соразмерности, соответствия основным гигиеническим принципам, снижения воздействия негативных факторов окружающей среды, сохранения здоровья.
Рецензенты:
Камалян Р.З., д.т.н., профессор кафедры математики и вычислительной техники Академии ИМСИТ, г. Краснодар.
Усатиков С.В., д.ф.-м.н., профессор кафедры информационных образовательных технологий Кубанского государственного университета г. Краснодар.
Библиографическая ссылка
Иващенко И.Н., Шмалько С.П. РЕГРЕССИОННЫЕ МОДЕЛИ И ОПТИМИЗАЦИЯ СУММАРНОГО ТЕПЛОВОГО СОПРОТИВЛЕНИЯ ПОКРОВНЫХ МАТЕРИАЛОВ ОДЕЖДЫ ДЛЯ НЕФТЯНИКОВ // Современные проблемы науки и образования. 2014. № 3. ;URL: https://science-education.ru/ru/article/view?id=13517 (дата обращения: 11.02.2026).



