Введение. Моделирование и оптимизация параметров и режимов на всех этапах жизненного цикла и на всех уровнях организации, функционирования и управления представляет собой задачу большой размерности. Одним их путей решения таких задач является привлечение эффективного аппарата многокритериальной оптимизации (МКО).
Существующее математическое обеспечение характеризуется узкой направленностью, связанной с конкретной предметной областью и жестко заложенными численными схемами и алгоритмами, и, как правило, основано на случайном выборе или различных способах дискретизации. При этом нет объективных оснований, почему был сделан выбор той или иной части множества вариантов [1-3].
Теоретический обзор. Итерационный процесс решения модели предполагает наличие нескольких этапов выбора. Не теряя общности, можно формализовать общую модель задачи выбора решений на итерациях поиска, как:
![]() , (1)
, (1)
где ![]() – номер текущей итерации;
– номер текущей итерации; ![]() – исходное множество решений, предъявляемых для выбора;
– исходное множество решений, предъявляемых для выбора; ![]() – вектор показателей качества решений;
– вектор показателей качества решений; ![]() – совокупность сведений, задающих специфические свойства рассматриваемой модели;
– совокупность сведений, задающих специфические свойства рассматриваемой модели; ![]() – функция выбора.
– функция выбора.
Требуется в соответствии с свойствами ![]() синтезировать механизм выбора
синтезировать механизм выбора ![]() , определяющий соответствующую функцию выбора
, определяющий соответствующую функцию выбора ![]() . Если за
. Если за ![]() принять множество решений после применения процедуры отсева на итерации поиска, то можно рассмотреть получение искомого множества
принять множество решений после применения процедуры отсева на итерации поиска, то можно рассмотреть получение искомого множества ![]() из исходного
из исходного ![]() на итерациях поиска как последовательное преобразование (сужение) множества
на итерациях поиска как последовательное преобразование (сужение) множества ![]() :
:
![]() ,
,
где ![]() – допустимое множество рассматриваемых решений (альтернатив) на i-й итерации поиска,
– допустимое множество рассматриваемых решений (альтернатив) на i-й итерации поиска, ![]() – множество недоминируемых альтернатив,
– множество недоминируемых альтернатив, ![]() .
.
Таким образом, ситуация отсева решения на итерациях поиска, приведенная на рисунке 1, представляет собой двухэтапную процедуру, на каждой итерации которой происходит генерация множества Парето (построение множества ![]() ), а затем отсев (получение множества
), а затем отсев (получение множества ![]() ) для контроля роста его мощности, т.е. необходимо определить механизмы выбора
) для контроля роста его мощности, т.е. необходимо определить механизмы выбора ![]() и
и ![]() , которые в соответствии со свойствами
, которые в соответствии со свойствами ![]() порождали бы соответственно функции выбора
порождали бы соответственно функции выбора ![]() [1-3].
[1-3].
Методика. На первом шаге в качестве механизмов выбора, порождающих функцию выбора ![]() , могут выступать процедуры формирования множества допустимых вариантов, удовлетворяющих соответствующим техническим, технологическим и другим ограничениям области D.
, могут выступать процедуры формирования множества допустимых вариантов, удовлетворяющих соответствующим техническим, технологическим и другим ограничениям области D.
Функция выбора ![]() на втором шаге порождается классом многоэкстремизационных механизмов выбора
на втором шаге порождается классом многоэкстремизационных механизмов выбора ![]() , в которых роль структуры
, в которых роль структуры ![]() играет вектор
играет вектор ![]() , а в качестве правила выбора
, а в качестве правила выбора ![]() могут выступать различные принципы выделения недоминируемых альтернатив [4-7].
могут выступать различные принципы выделения недоминируемых альтернатив [4-7].
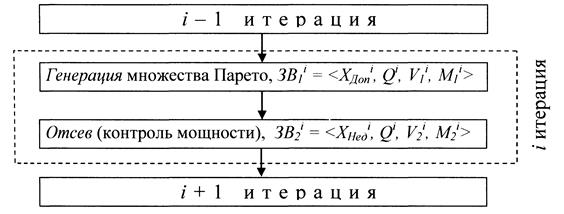
Рисунок 1 – Этапы решения задачи выбора на итерациях
Рассмотрим механизмы выбора, свойства которых позволяют применять их для отбора решений на итерациях поиска в моделях МКО для этапа формирования множества ![]() и
и ![]() .
.
Механизм выбора равномерно-распределенных точек. В большинстве численных схем на первом шаге оптимизации применяются различные способы построения первоначального множества вариантов решения. Однако этот процесс также представляет собой типичную ситуацию выбора части вариантов из исходного множества. Поэтому предложим такие условия отбора в виде механизма выбора.
При решении численной схемы МКО на первом шаге каждой ![]() итерации, согласно некоторому генератору Г, из исходной области решений
итерации, согласно некоторому генератору Г, из исходной области решений ![]() предлагается строить текущее множество вариантов решения задачи Х:
предлагается строить текущее множество вариантов решения задачи Х: ![]() . В качестве генератора Г предлагается конкретная численная схема в том или ином методе оптимизации, но так как при любом способе построения
. В качестве генератора Г предлагается конкретная численная схема в том или ином методе оптимизации, но так как при любом способе построения ![]() , в конечном счете, происходит выбор подмножества из исходного множества вариантов, естественным было бы описание оператора Г в терминах теории выбора. Если рассмотреть
, в конечном счете, происходит выбор подмножества из исходного множества вариантов, естественным было бы описание оператора Г в терминах теории выбора. Если рассмотреть ![]() в качестве множества исходных вариантов, а
в качестве множества исходных вариантов, а ![]() - непустое множество, предъявленное для выбора, то механизм выбора из D по некоторому правилу С части вариантов формализуем в виде [2-3]:
- непустое множество, предъявленное для выбора, то механизм выбора из D по некоторому правилу С части вариантов формализуем в виде [2-3]:
![]() . (2)
. (2)
Множество ![]() в формуле (3.28), это набор элементов, удовлетворяющих условиям:
в формуле (3.28), это набор элементов, удовлетворяющих условиям:
![]() , (3)
, (3)
где П – некоторый оператор, задающий условие выбора.
В соответствии с [5], для формализации механизма выбора М необходимо знать структуру исходного множества, а также задать правило выбора ![]() , которое указывает, как построить функцию С(Х) для любого
, которое указывает, как построить функцию С(Х) для любого ![]() на основе данной структуры. Здесь
на основе данной структуры. Здесь ![]() , т.е. множество всех непустых подмножеств
, т.е. множество всех непустых подмножеств ![]() мощность D).
мощность D).
Согласно формуле (3), правило выбора ![]() формализуем в виде [6]:
формализуем в виде [6]:
![]() . (4)
. (4)
Конкретная реализация С и ![]() для механизма выбора равномерно-распределенных точек на примере модели перераспределения плотности вероятности рассмотрена ниже.
для механизма выбора равномерно-распределенных точек на примере модели перераспределения плотности вероятности рассмотрена ниже.
Независимо от исходной области поиска (дискретной или непрерывной), на итерациях получается дискретный набор недоминируемых вариантов решения X.
Определим на нем значения критериальных функций ![]() . Через
. Через ![]() обозначим значение
обозначим значение ![]() -й критериальной функции в точке
-й критериальной функции в точке ![]() . Будем считать, что
. Будем считать, что ![]() тогда и только тогда, когда
тогда и только тогда, когда ![]() . Пронумеруем числа
. Пронумеруем числа ![]() в порядке убывания. Если при этом встретятся равные, то нумеруем их в порядке убывания следующей координаты. Если (п-1) координата двух точек совпадает, то выводим из рассмотрения точку, имеющую меньшую п-ю координату. Аналогично нумеруем последующие координаты
в порядке убывания. Если при этом встретятся равные, то нумеруем их в порядке убывания следующей координаты. Если (п-1) координата двух точек совпадает, то выводим из рассмотрения точку, имеющую меньшую п-ю координату. Аналогично нумеруем последующие координаты ![]() .
.
В результате такого отображения мы поставили в соответствие точкам множества допустимых оценок Y, множество ![]() -точек с координатами
-точек с координатами ![]() , каждая из которых принимает целое значение их интервала [1, ...,р]. При этом в каждой из гиперплоскостей размерности n-1, параллельных координатным, одна и только одна из точек этого множества. Множество лежит в п-мерном кубе размером
, каждая из которых принимает целое значение их интервала [1, ...,р]. При этом в каждой из гиперплоскостей размерности n-1, параллельных координатным, одна и только одна из точек этого множества. Множество лежит в п-мерном кубе размером ![]() [4-6].
[4-6].
В силу построения любая точка множества ![]() лежит на пересечении
лежит на пересечении ![]() гиперплоскостей размерности
гиперплоскостей размерности ![]() , параллельных координатным гиперплоскостям и проходящим через точки
, параллельных координатным гиперплоскостям и проходящим через точки ![]() . По той же причине из
. По той же причине из ![]() следует, что
следует, что ![]() , а значит, выше точек, оптимальных по Парето, на множестве значений критериев оптимизации Y эквивалентно аналогичной операции в множестве
, а значит, выше точек, оптимальных по Парето, на множестве значений критериев оптимизации Y эквивалентно аналогичной операции в множестве ![]() , только в смысле сравнения
, только в смысле сравнения ![]() .
.
Для того чтобы точка множества ![]() принадлежала множеству Парето, необходимо, чтобы ее координаты удовлетворяли условию [5]:
принадлежала множеству Парето, необходимо, чтобы ее координаты удовлетворяли условию [5]:
![]() (5)
(5)
Алгоритм построения множества Парето.
1. Описанным выше способом строим множество ![]() эквивалентное множеству Y допустимых оценок. При этом каждую из координат упорядочиваем методом деления отрезка пополам.
эквивалентное множеству Y допустимых оценок. При этом каждую из координат упорядочиваем методом деления отрезка пополам.
Каждой точке множества ![]() ставим в соответствие последовательность счетчиков
ставим в соответствие последовательность счетчиков ![]() /
/
3. Отбросим точки, не удовлетворяющие условию (5). При каждом отбрасывании координаты точек множества ![]() большие соответствующей координаты отбрасываемой точки уменьшается на единицу, настолько же уменьшится и соответствующая сумма [7-9].
большие соответствующей координаты отбрасываемой точки уменьшается на единицу, настолько же уменьшится и соответствующая сумма [7-9].
4. У точки лучше отбрасываемой сумма координат не изменится, хотя число р уменьшится на единицу; а у конфликтующей точки сумма координат уменьшится не более чем на n-1, хотя левая часть неравенства уменьшится на n-1.
Введем утверждение. Точки лучшие или конфликтующие с отбрасываемой, лежавшие выше границы точек, оптимальных по Парето, никогда не перейдут этой границы.
5. Таким образом, при отбрасывании точки, для которой выполнено неравенство: 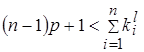 , обладающие таким же свойством, не перейдут через границу точек, оптимальных по Парето. После того, как все точки будут удовлетворять условию (5), упорядочим последовательность сумм координат оставшихся точек. Точки, имеющие минимальную сумму, а также сумму, отличающуюся не более чем на n-1, оптимальны по Парето. Запоминаем их и выводим из рассмотрения, уменьшая описанным выше способом координаты и суммы координат остающихся точек [10].
, обладающие таким же свойством, не перейдут через границу точек, оптимальных по Парето. После того, как все точки будут удовлетворять условию (5), упорядочим последовательность сумм координат оставшихся точек. Точки, имеющие минимальную сумму, а также сумму, отличающуюся не более чем на n-1, оптимальны по Парето. Запоминаем их и выводим из рассмотрения, уменьшая описанным выше способом координаты и суммы координат остающихся точек [10].
При каждом уменьшении координаты некоторой точки увеличиваем на единицу соответствующий ей счетчик. Если у точки счетчик окажется равным n, то её также отбрасываем, прежде чем приступить к выводу из рассмотрения очередной точки, оптимальной по Парето.
7. Процесс повторяется до тех пор, пока оставшиеся точки будут иметь суммы, отличающиеся от минимальной не более чем на ![]() и удовлетворять условию:
и удовлетворять условию: 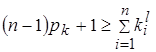 , где
, где ![]() – число оставшихся точек.
– число оставшихся точек.
Алгоритм выделения множества Парето при n=2.
1. Описанным выше способом строим множество (![]() ), эквивалентное множеству
), эквивалентное множеству ![]() допустимых оценок. При этом упорядочивание по каждой из двух координат проводим методом деления отрезка пополам.
допустимых оценок. При этом упорядочивание по каждой из двух координат проводим методом деления отрезка пополам.
2. Каждой точке множества (![]() ) ставим в соответствие последовательность сумм координат (
) ставим в соответствие последовательность сумм координат (![]() ). Если все
). Если все ![]() , то любая точка множества, а значит, и множества
, то любая точка множества, а значит, и множества ![]() оптимальна по Парето. В противном случае существует, по крайней мере, одна точка, удовлетворяющая условию
оптимальна по Парето. В противном случае существует, по крайней мере, одна точка, удовлетворяющая условию ![]() . Пусть эта точка (
. Пусть эта точка (![]() ). Отбрасываем ее.
). Отбрасываем ее.
3. Тогда точки с координатами ![]() или
или ![]() будут иметь координаты
будут иметь координаты ![]() или
или ![]() . Каждое уменьшение координаты приводит к уменьшению суммы координат. Число р заменяется
. Каждое уменьшение координаты приводит к уменьшению суммы координат. Число р заменяется ![]() . Если некоторая точка (
. Если некоторая точка (![]() ) лучше отбрасываемой, то ее сумма координат останется прежней, хотя число
) лучше отбрасываемой, то ее сумма координат останется прежней, хотя число ![]() в неравенстве заменится на
в неравенстве заменится на ![]() . Если точка (
. Если точка (![]() ) хуже отбрасываемой, то ее сумма координат уменьшится на 2; если точка (
) хуже отбрасываемой, то ее сумма координат уменьшится на 2; если точка (![]() ) конфликтует с отбрасываемой, то неравенство сохранится [].
) конфликтует с отбрасываемой, то неравенство сохранится [].
Отсюда следует, что точки, лучшие или конфликтующие по отношению к отбрасываемой и не являющиеся оптимальными по Парето, будут на некотором шаге отброшены. Остается показать, что ни одна из худших точек по отношению к отбрасываемой на любом u-том шаге не достигнет границы ![]() . Действительно, если мы отбрасываем точку (
. Действительно, если мы отбрасываем точку (![]() ), то имеет место неравенство:
), то имеет место неравенство: ![]() или
или ![]() .
.
Так как точка (![]() ) хуже точки (
) хуже точки (![]() ), то имеют место неравенства:
), то имеют место неравенства:
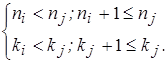
При отбрасывании лучшей точки у худшей сумма координат уменьшается на 2, новая сумма координат точки (![]() ) равна (
) равна (![]() ), при этом, однако,
), при этом, однако, ![]() . Так как
. Так как ![]() то
то ![]() , или окончательно
, или окончательно ![]() .
.
5. Таким образом, процесс отбрасывания худших точек продолжается до тех пор, пока не останется точек, удовлетворяющих условию ![]() . Тогда все оставшиеся точки в силу теоремы 4 будут оптимальны по Парето.
. Тогда все оставшиеся точки в силу теоремы 4 будут оптимальны по Парето.
Вывод. Проведенный эксперимент подтверждает адекватность построения данного алгоритма, причем скорость поиска на множестве Парето большой мощности существенно выше, без потери качества решения, по сравнению с аналогами (в частности, с рассматриваемым в работе методом перераспределения плотности вероятности).
Рецензенты:
Кондрашова Е.В., д.т.н., профессор кафедры технического сервиса и технологии машиностроения ФГБОУ ВПО «Воронежский государственный аграрный университет имени императора Петра I», г. Воронеж.
Зольников В.К., д.т.н., профессор, заведующий кафедрой информатики и вычислительной техники ФГБОУ ВПО «Воронежская государственная лесотехническая академия», г. Воронеж.
Библиографическая ссылка
Скрыпников А.В., Яковлев К.А. ИТЕРАЦИОННЫЙ ПРОЦЕСС РЕШЕНИЯ МОДЕЛИ // Современные проблемы науки и образования. 2014. № 4. ;URL: https://science-education.ru/ru/article/view?id=13463 (дата обращения: 06.03.2026).



