Керамические материалы широко применяются в приборостроении, ядерной энергетике, ракетной и аэрокосмической технике, химической промышленности и машиностроении, например газотурбинные установки, гироскопы, режущий инструмент, броневая защита военной техники, тепловая защита головных частей ракет и космических кораблей, футеровка реакторов и различные элементы пар трения. Керамические материалы обладают высокими жаро- и кислотостойкостью, износостойкостью, твердостью, малой плотностью и др.
В последнее время исследованиям в сфере изготовления и обработки керамических материалов уделяется все большее внимание. Ведущее место в мире занимает японская керамическая промышленность. Открываются центры по разработке и исследованию керамических материалов, например, центр конструкционной керамики в Пенсильванском университете в США. В России открыты государственные предприятия и центры, например, ФГУП "ОНГШ "Технология" ГНЦ РФ (г. Обнинск) по разработке конструкционной керамики из нитрида и карбида кремния, нитрида бора, оксида алюминия, диоксида циркония, различных композиций и применению ее при изготовлении космических аппаратов, ракет-носителей, самолетов и др. техники. Научно-производственная фирма ИРИТО (г. Москва) производит изделия из карбида кремния. ООО ВИРИАЛ (Санкт-Петербург) производит машиностроительную износостойкую керамику на основе модифицированного карбида кремния, композиционные материалы на основе стекло - и углеродных волокон. [5]
Керамические материалы при спекании имеют достаточно большую усадку. При черновом шлифовании керамических заготовок снимаемый слой составляет от десятых долей до нескольких миллиметров. Основная задача чистового шлифования заключается в придании заготовки определенной геометрической формы и снятии дефектного слоя, образовавшемся при черновой обработке. Далее следует доводка, которая обеспечивает необходимое качество поверхности.
Для получения высококачественных поверхностей деталей из керамических материалов используется, в основном, шлифование алмазными кругами. Процесс съема керамического материала отличается от процесса шлифования металлов. При обработке шлифованием керамических материалов на поверхности появляются трещины, проникающие на некоторую глубину. Эти трещины пересекаются между собой, создавая механически ослабленный слой, который легко разрушается при дальнейшем воздействии абразива. Шлифование керамических материалов осложняется их склонностью к растрескиванию, отсутствию пластичности, высокой твердостью, низкой стойкостью к тепловым ударам и т.д.
Для обработки плоских керамических заготовок широко применяется универсальное плоскошлифовальное оборудование. При изготовлении деталей из хрупких высокотвердых материалов на таком оборудовании возникает ряд существенных проблем: сквозное растрескивание заготовок, большой процент брака из-за невыполнения жестких требований к точности размеров, шероховатости поверхностей, неэкономичный расход дефицитных материалов, невысокая производительность технологий и т.п. [5].
В настоящее время режимы шлифования керамических материалов выбираются в соответствии с рекомендациями, предложенными в работах Н. В. Никиткова, А. В. Балыкова и других ученых. Разработка высокоэффективных методов механической обработки керамических материалов является одной из сложнейших задач современного машиностроения.
Рассмотрим процесс алмазного шлифования с помощью анализа размерностей. В качестве основных единиц используем по международной системе единиц (СИ) измерения массы M [кг], длины L [м] и времени T [сек]. Для описания состояние механической системы найдем уравнения движения и величины входящие в эти уравнения. Выявим совокупность параметров, которые однозначно характеризуют процесс алмазного шлифования. С помощью этих переменных в процессе анализа размерностей получим безразмерные комплексы.
Цель анализа размерностей - дать некоторые сведения о соотношениях, существующих между измеримыми величинами, связанными с различными явлениями. Преимущество метода в его быстроте, он избавляет от необходимости производить полный анализ задачи, нет надобности, например, выписывать уравнения движения механической системы. С другой стороны, анализ размерностей дает далеко не все сведения, которые могут быть получены при детальном рассмотрении [1].
В совокупность переменных входят величины, характеризующие геометрические и некоторые качественные параметры шлифовального круга и факторы режима обработки – скорость шлифования V и давление круга на заготовку q.
Скорость шлифования V и давление круга на заготовку q однозначно определяют состояние системы. Величиной, характеризующей геометрические и некоторые качественные параметры алмазного шлифовального круга, является эффективная площадь контакта F шлифовального круга с обрабатываемой заготовкой. Эффективную площадь F представим как площадь сечения режущих алмазных зерен плоскостью перпендикулярной оси вращения шлифовального круга на высоте 0,15W от режущей кромки, где W – зернистость алмазного порошка (рисунок 1). Примем форму единичного алмазного зерна за октаэдр, диагональ которого равна зернистости W, а длина ребра равна ![]() . При благоприятном режиме шлифования деталь не контактирует со связкой алмазного шлифовального круга, а режущее зерно внедряется в обрабатываемый материал на 0,2-0,4 выступающей части. С учетом глубины заделки зерна в связку равной не более 0,5W, глубина внедрения зерна в обрабатываемый материал 0,1-0,2 W (в среднем 0,15W). Площадь сечения единичного зерна на высоте 0,15W является площадью контакта зерна с обрабатываемой заготовкой.
. При благоприятном режиме шлифования деталь не контактирует со связкой алмазного шлифовального круга, а режущее зерно внедряется в обрабатываемый материал на 0,2-0,4 выступающей части. С учетом глубины заделки зерна в связку равной не более 0,5W, глубина внедрения зерна в обрабатываемый материал 0,1-0,2 W (в среднем 0,15W). Площадь сечения единичного зерна на высоте 0,15W является площадью контакта зерна с обрабатываемой заготовкой.
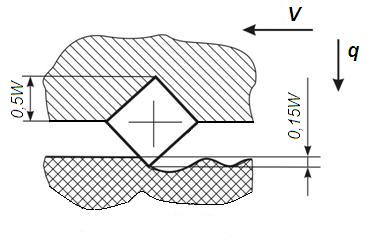
Рисунок 1 – Внедрения единичного зерна в обрабатываемый материал.
Эффективная площадь F зависит от фактической площади контакта алмазного шлифовального круга с заготовкой, зернистости W и концентрации C применяемого алмазного порошка.
Применение эффективной площади контакта шлифовального круга с обрабатываемой заготовкой F, зависящей от указанных выше переменных, позволяет применять результаты моделирования на алмазные шлифовальные круги широкого диапазона диаметров, формы, зернистости и концентрации алмазов.
В качестве переменной, характеризующей диспергирование керамического материала в ходе процесса алмазного шлифования, примем режущую способность шлифовального круга Q. Так же необходимо учесть микротвердость HV обрабатываемого керамического материала.
Процесс алмазного шлифования керамических материалов кругами с заданными маркой, концентрацией алмазов и связкой достаточно полно можно описать следующими физическими величинами: скорость шлифования V, давление круга на заготовку q, эффективная площадь контакта F, режущая способность круга Q, твердость обрабатываемого материала HV. Все эти величины или являются заданными, как твердость обрабатываемого материала HV, или легко определяются, как q и Q, и рассчитываются, как V и F.
Запишем выбранные определяющие физические величины в таблицу и укажем формулы размерности.
Таблица 1
Физические величины, характеризующие процесс алмазного шлифования и формулы их размерности
|
Физическая величина |
Символ |
Формула размерности |
|
Скорость шлифования |
V |
LT -1 |
|
Режущая способность круга |
Q |
L3T -1 |
|
Давление круга на заготовку |
q |
ML -1T -2 |
|
Эффективная площадь контакта круга с обрабатываемой деталью |
F |
L2 |
|
Твердость |
HV |
ML -1T -2 |
Режущая способность круга Q является основным фактором, влияющий на процесс диспергирования керамического материала при алмазном шлифовании. Представим режущую способность круга Q как функцию от других величин, выбранных для описания процесса алмазного шлифования:
Q=f(V, q, F, HV) (1)
Следуя π-теореме теории подобия найдем безразмерные степенные комплексы. Теорема утверждает, что если имеется зависимость между n физическими величинами, не меняющая своего вида при изменении масштабов единиц в некотором классе систем единиц, то она эквивалентна зависимости между меньшим числом p=n–k безразмерных величин, где k — наибольшее число величин с независимыми размерностями среди исходных n величин. p-теорема позволяет установить общую структуру зависимости, вытекающую только лишь из требования инвариантности физической зависимости при изменении масштабов единиц, даже если конкретный вид зависимости между исходными величинами неизвестен [9].
Определим безразмерные степенные комплексы, используя метод Релея [1] для решения размерных систем.
Предположим, существует соотношение:
![]() (2)
(2)
Запишем формулу (2) используя размерности этих величин:
![]() (3)
(3)
Составим соотношения для показателей степени, при выполнении которых уравнение (3) будет однородным по размерностям:
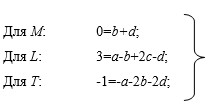
Решив данную систему уравнений, получим:
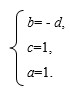
Подставим найденные значения показателей степеней в исходное уравнение (2), получаем:
![]()
или
![]() (4)
(4)
Из (4) получаем безразмерные комплексы:
π1= q/HV (5)
и
π2= Q/V∙F (6)
Для описания процесса алмазного шлифования керамических материалов шлифовальным кругом с определенными размерами круга, маркой и концентрацией алмазного порошка достаточно выявить зависимость между найденными числами подобия π1= q/HV и π2= Q/V∙F.
Для упрощения модели ![]() , пользуясь предложенной Ю. Н. Полянчиковым, Е. М. Фроловым и Д. С. Клюйковым методологией построения и анализа регрессионных моделей [7], получим регрессию.
, пользуясь предложенной Ю. Н. Полянчиковым, Е. М. Фроловым и Д. С. Клюйковым методологией построения и анализа регрессионных моделей [7], получим регрессию.
Коэффициенты уравнения регрессии b и a можно определить по методу наименьших квадратов по следующим формулам:
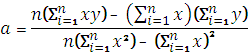 , (7)
, (7)
![]() , (8)
, (8)
где y – значение функции отклика в i-м опыте; x – значение фактора в i-м опыте; n – число опытов.
Главным преимуществом данной математической модели является, то, что она дает возможность оценить влияние факторов режима обработки – скорости шлифования V и давления круга на заготовку q, а также их взаимовлияния на основные параметры процесса алмазного шлифования керамических материалов. Найденная математическая модель позволяет построить методику проведения экспериментов для определения рациональных режимов алмазного шлифования торцов керамических подшипников. Найденные рациональные режимы алмазного шлифования керамических материалов позволят увеличить долговечность и надежность керамических подшипников.
Рецензенты:
Бурлаченко О.В., д.т.н, профессор, проректор по учебно-воспитательной работе Волгоградского государственного архитектурно-строительного университета, заведующий кафедрой «Технологии строительных производств» ВолгГАСУ, г. Волгоград.
Труханов В.М., д.т.н., профессор кафедры «Автоматизация производственных процессов», Волгоградский государственный технический университет, г. Волгоград.
Библиографическая ссылка
Сердобинцев Ю.П., Харьков М.Ю., Наззал А.С. МОДЕЛИРОВАНИЕ ПРОЦЕССА АЛМАЗНОГО ШЛИФОВАНИЯ ТОРЦОВ КЕРАМИЧЕСКИХ ПОДШИПНИКОВ // Современные проблемы науки и образования. 2014. № 3. ;URL: https://science-education.ru/ru/article/view?id=13405 (дата обращения: 28.12.2025).



