Современный специалист, оканчивающий вуз, и взявший на вооружение третий метод познания – математическое моделирование, в определённом смысле может быть уподоблен лётчику-любителю, получающему пилотское свидетельство. Он научился взлетать и приземляться, выбирать курс и эшелон полёта и обучен ряду лётных премудростей, но из этого не следует, что он разбирается в теоретических вопросах аэродинамики и инженерных тонкостях самолётостроения, - он классический современный пользователь авиатехники. Наша цель: дать студенту-старшекурснику аналогичный пользовательский багаж приёмов и инструментов, необходимых при построении математических моделей и проведении с ними вычислительных экспериментов для получения важных исследовательских результатов в интересующей области, в данном случае – в экологии.
Описанная в работе [6] методология и методика математического моделирования в экологии обрела неукротимый потенциал роста после того, как было создано несколько математических пакетов, сразу завоевавших статус модельных конструкторов, - «Математика», Mathlab, Мapl и MathCad. Наиболее простым и доступным в освоении даже представителям гуманитарных профессий – социологам, экономистам, психологам и экологам - оказался последний из представленного списка. На рабочем поле этого конструктора записываются системы уравнений, начальные данные и коэффициенты модели практически так же, как мелом или маркером на доске, а затем ставится вычислительный эксперимент, и сразу можно получить динамические графики и фазовые диаграммы.
В этой же публикации [6] в качестве простейшего примера, иллюстрирующего применение названного математического аппарата к анализу экологической ситуации в промышленной зоне крупного города, приведён знаковый ориентированный граф, где в его вершинах записаны переменные модели:
Х1 (З(1)) – число заводских предприятий в промышленной зоне города;
Х2 (Н) – численность населения города;
Х3 (Р(3)) – численность рабочих мест;
Х4 (С(4)) – показатель состояния окружающей среды – процент её загрязнения. Переменные влияют друг на друга так, как это показано дугами орграфа (рис. 1).
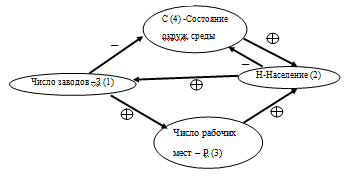
Рис. 1. Орграф связей между переменными макромодели города.
В модели, представленной на графе, прочитывается отрицательная обратная связь, стабилизирующая экологическую ситуацию: рост числа заводских предприятий - З(Х1) негативно (знак минус на дуге) влияет на состояние окружающей среды – С(Х4); пропорционально её ухудшению идёт уменьшение численности населения города – Н(Х2); уменьшение численности населения Н(Х2) ведёт к банкротству и закрытию части заводов - З(Х1), т.е. и к уменьшению Р(Х3); поскольку дуга З(Х1) - С(Х4) несёт на себе отрицательный знак, то выше описанное в контуре уменьшение численности заводов приводит к улучшению экологической ситуации, а далее цикл повторяется. Примеры подобного применения знаковых ориентированных графов, более сложные по характеру и решающие прикладные эколого-экономические проблемы, содержатся в списке литературы [1-5].
Опыт обучения студентов по дисциплинам «Социальное прогнозирование и проектирование», «Математическое моделирование социальных процессов», «Математические модели в гуманитарных науках» показал, что наиболее целесообразно начинать эти дисциплины с именно с когнитивного моделирования на ориентированных графах [1; 4]. Именно элементарная топология позволяет содержательное описание процесса или явления представить через набор взаимодействующих факторов, а затем двигаться в направлении построения дискретной системы рекуррентных уравнений, описывающих динамику процесса или изменений явления. При наличии подходящих условий и соответствующих эмпирических референтов эта система может преобразоваться или в конечно-разностные уравнения - КРУ, или в систему обыкновенных дифференциальных уравнений – ОДУ.
Условием перехода СРС в конечно-разностные уравнения (КРУ) являются требования (на примере 2-слойной схемы; в целом рассматриваются модели процессов с числом слоев ≤ 3):
Xn+1 = Xn + τ*F(tn, Xn), где tn = n*τ, где τ - шаг квантования времени
Условием перехода КРУ в ОДУ – обыкновенные дифференциальные уравнения - является существование конечного предела:
lim (Xn+1 - Xn )/(tn+1 - tn ) < ∞ при (tn+1 - tn)= τ → 0
Для системы ОДУ на конечном интервале времени всегда может быть поставлена и решена задача Коши – ЗК или краевая задача - КЗ, т.е. по начальным и граничным условиям рассчитываются значения X(t). Однако в случае плохой обусловленности матрицы оператора системы ОДУ или КРУ, что зачастую вполне вероятно из-за совмещения в одном процессе быстрых и медленных переменных, эффективный прогноз возможен только на весьма ограниченном отрезке времени [8]. Принято считать, что число обусловленности (conde) должно быть не более 400-500. Смысл этого числа в оценке скорости роста ошибки прогноза значений переменных модели.
С этой постановкой вопроса корреспондирует проблема устойчивости моделируемого социального процесса или проблема устойчивости процесса воспроизводства возникшей в новом ноосферном порядке некоторой типичной целостности, например биоценоза. «Кратко, устойчивость – У. движения системы может пониматься как свойство «а) движущейся системы… мало отклоняться от некоторого движения при малых возмущениях начального положения системы (в фазовом пространстве), причём малость отклонения равномерна по t≥0 (У. по Ляпунову, Орбитальная устойчивость)»; б) «системы сохранять некоторые черты фазового портрета при малых возмущениях закона движения» (Структурная устойчивость, грубая система); в) «системы в процессе движения оставаться в ограниченной области фазового пространства» (У. по Лагранжу); г) «системы в процессе движения сколь угодно поздно возвращаться как угодно близко к своему начальному положению (в фазовом пространстве)» (У. по Пуассону), - ясно, что это не все виды У» [8]. Однако MathCad позволяет пользователю достаточно легко определиться с решением проблемы устойчивости описываемого явления или конструируемого механизма некоторого процесса. Но начнём по порядку с описания самой модели.
Э к о л о г и я г о р о д а 2014
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
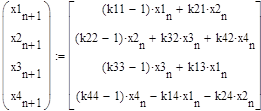
Система конечно-разностных уравнений откалибрована так, что описывает достаточно узнаваемый в динамических графиках сценарий развития современного среднерусского города, попавшего в посткризисную ситуацию после 2008-09 гг. (рис. 2-5).
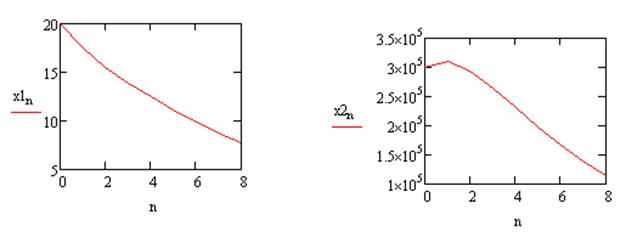
Рис. 2. Динамика численности заводов. Рис. 3. Динамика численности населения.
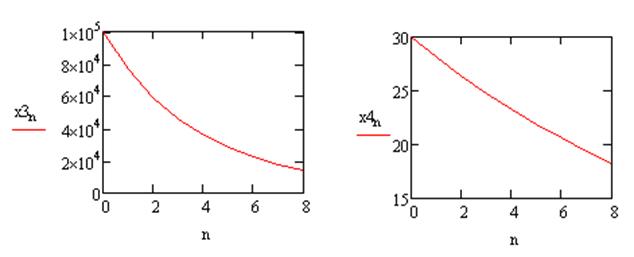
Рис. 4. Динамика численности рабочих мест. Рис. 5. Динамика степени загрязнения (%).
Чтобы выяснить, обладает ли построенная и откалиброванная система КРУ каким-либо видом устойчивости, для написанной системы конечно-разностных уравнений модели сначала строится квадратная 4х4 матрица М оператора системы уравнений. Как её строить, легко уразуметь, разглядывая систему КРУ. Построив матрицу М, опускаем курсор ниже матрицы и к её правому углу. Далее с помощью функции f(x), кнопка для которой расположена во второй сверху строке, нажав её, открываем окно с меню, в котором находим слова «векторы и матрицы». Подведя курсор к строке с этими словами и нажав на ввод, открываем окно с дополнительным меню, в котором находим слово eigenvals и также, используя курсор и клавишу «ввод», выводим eigenvals (). Поставив в ячейку, которая обнаруживается в скобках символ М, сдвигаем синий уголок так, чтобы он оказался на строке eigenvals (М) справа самым крайним. После этого, вызвав нажатием на кнопку с изображением калькулятора, находим на калькуляторе в правом нижнем углу знак = и нажимаем «ввод». Тотчас под матрицей справа от eigenvals (М) = появится столбец с набором «собственных значений» матрицы М (рис. 6).

Рис. 6. Матрица М оператора системы КРУ и вектор её собственных значений.
Если все действительные части компонент этого вектора отрицательны, то система обладает устойчивостью по Ляпунову. Если хотя бы в одном случае будут положительные величины, то таковой устойчивости нет. Если модули всех компонент собственных значений меньше 1, как в нашем случае, то система уравнений модели обладает устойчивостью по Лагранжу. Кстати, в нашем случае число обусловленности неважное, и оно равно 2.904 104.
Довольно долго, главным образом под влиянием авторитета французского математика – создателя теории катастроф Рене Тома и исходя из того, что процессы в естественных науках породили представления об устойчивых стационарных моделях как основе описания явлений мира, господствовала точка зрения, что в реальности значение имеют только устойчивые процессы, т.е. существующее устойчиво.
Однако исследования сложных систем в науках о живой материи (биологии, физиологии, психологии и т.д.) и неравновесных процессов в физике, физической химии обосновали другой заглавный постулат: предсказуемость существующего, что допускает ценность и неустойчивых процессов.
Тем не менее, если модельер берётся конструировать какой-то механизм, то в этом случае, безусловно, необходимо представить устойчивую реализацию, хотя бы частичную.
Рецензенты:
Шведовский В.А., д.соц.н., социологический факультет МГУ им. М.В. Ломоносова, г.Москва.
Невская Г. Ф., д.м.н., профессор, зав. кафедрой «Безопасность и экология», МГОУ, г.Москва.
Библиографическая ссылка
Шведовская Т.Л., Владимиров С.Н. О ПЕРСПЕКТИВНЫХ НАПРАВЛЕНИЯХ И СРЕДСТВАХ ПРЕПОДАВАНИЯ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ В ЭКОЛОГИИ // Современные проблемы науки и образования. 2014. № 3. ;URL: https://science-education.ru/ru/article/view?id=13394 (дата обращения: 05.01.2026).



