Введение
Инженерно-геологические условия занимают особое место в проблемах фундаментостроения и в Западной Сибири. Большая часть территории севера Западной Сибири заторфована, а значительная часть юга этого региона сложена слабыми водонасыщенными пылевато-глинистыми грунтами, поэтому достаточно часто при проектировании фундаментов под здания средней и повышенной этажности в Западной Сибири появляется проблема выбора типа фундамента.
Основной величиной, определяющей возможность использования фундамента мелкого заложения для определенного здания в определенных инженерно-геологических условиях, является осадка s и производная от нее – неравномерность осадки Δs/L, где L – расстояние между отдельными частями здания или сооружения.
Осадки и особенно их неравномерность зависят от закона распределения давлений на грунтовое основание. Управляя законом распределения контактных давлений, можно получить требуемое напряженно-деформированное состояние грунтового основания и обеспечить нормируемые параметры. Это можно добиться путем создания фундамента, состоящего из различных по жесткости и характеру работы элементов (рис. 1). Первый – ленточный фундамент, опорная конструкция для несущих стен или колонн, обладающий определенной жесткостью в продольном направлении, воспринимающий случайные эксцентриситеты передачи нагрузки, формирующий требуемые консольные уширения по наружному контуру здания. Второй – гибкий элемент в пролетной части, обращенный выпуклостью вверх, объединяющий соседние опорные ленты в сплошной фундамент. Его функция заключается в передаче определенной (заданной) части нагрузки от сооружения на грунтовое основание в пролетной части. Основным качеством гибкого элемента должно быть достаточно быстрое реагирование закона распределения контактных давлений на изменение его конструктивных или геометрических параметров.
Рассматриваемые оболочечные гибкие связи между ленточными фундаментами имеют незначительный подъем по сравнению к размерам в плане 1/12<f/L < 1/5 и могут отнестись к категории пологих оболочек.
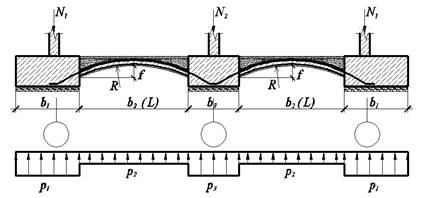
Рис.1. Ленточные фундаменты с гибкой связью
Постановка задачи
Необходимость расчета несущей способности оснований ленточных фундаментов, объединенных оболочками или мембранами, продиктована следующим.
Во-первых, согласно СП [5] и принятой в нашей стране практике проектирования расчеты оснований ведутся по двум группам предельных состояний. В СП есть методическое обеспечение как для определения расчетного сопротивления R, так и для определения несущей способности Nu одиночного ленточного фундамента. При этом отступления от указанной конкретной схемы часто сопряжены с необходимостью построения новых специальных решений. В этом отношении особенно остро стоит вопрос о несущей способности, поскольку решений теории предельного равновесия грунтов (ТПРГ) – главной теоретической базы для расчета несущей способности – известно сравнительно немного.
Во-вторых, в пп. 5.1.3, 5.7.5, 6.4.16 СП [5] указано, что для оснований, сложенных органоминеральными и органическими грунтами, а также медленно уплотняющимися водонасыщенными глинистыми грунтами (степень водонасыщения Sr³ 0,85 и коэффициент консолидации cv£ 107 см2/год), расчет по несущей способности обязателен. Поскольку исследуемые фундаменты применяются в основном именно в сложных инженерно-геологических условиях (на слабых грунтах), то построение для них специального решения является, по сути, требованием СП [5].
В-третьих, при построении решений ТПРГ приходится сталкиваться с рядом специфических проблем. Так, например, в ТПРГ не работает принцип суперпозиции. Это резко ограничивает возможности использования известных решений. В результате каждая конкретная задача требует специального, по существу, нового решения.
В-четвертых, как известно, МКЭ при определении предельной нагрузки не всегда дает стабильные результаты. О существовании такой проблемы говорится, например, в работах [2] и [7]. Следовательно, наличие надежной величины предельного давления дает возможность рассчитывать осадки за пределами стадии линейной деформируемости основания МКЭ с помощью различных нелинейных моделей грунта без риска превысить внешней нагрузкой в конечно-элементном решении предельное значение.
В-пятых, если учесть зарубежный опыт, то, помимо Eurocode 7 (где есть расчет только по несущей способности, но нет понятия расчетного сопротивления), следует упомянуть о значительном количестве работ, вышедших за последние годы, в которых рассматриваются задачи о несущей способности с позиций строгого статического метода ТПРГ, например [9, 10].
Таким образом, построение специальных решений ТПРГ для задач о несущей способности оснований ленточных фундаментов, объединенных оболочками, является актуальной задачей.
Алгоритм расчета оснований ленточных фундаментов, объединенных оболочками или мембранами по несущей способности
Прежде чем переходить к построению конкретных решений, следует сделать некоторые предварительные замечания, которые вытекают из специфических особенностей работы фундаментов, объединенных оболочками. При нагружении таких фундаментов нагрузка передается и на оболочки, и на ленточные фундаменты, и тем или иным образом перераспределяется между ними. Очевидно, что разрушение грунта будет происходить, прежде всего, именно под ленточными фундаментами. Поэтому имеет смысл выполнять расчет в следующей последовательности.
Первое. Определить соотношение давлений оболочки pоб и ленточные фундаменты pлент на основание.
Второе. Принять давление от оболочки на основание в качестве боковой пригрузки, т.е. q=pоб, для определения несущей способности основания под ленточным фундаментом.
Третье. Определить при q=pоб предельное давление ленточного фундамента на основание pu и сравнить его с давлением pлент.
Если pлент≤pu, то требование по несущей способности выполнено.
Итак, решение задачи о несущей способности грунтового основания ряда ленточных фундаментов, объединенных пологими оболочками, будем строить в рамках строгого статического метода ТПРГ. Плоская задача ТПРГ в декартовых координатах xOz (ось Oz направлена вертикально вниз) имеет вид:
![]() ,
, ![]()
![]() , (1)
, (1)
где g, j и c – удельный вес, угол внутреннего трения и удельное сцепление грунта.
Для решения конкретных задач систему уравнений (1) обычно преобразуют к каноническому виду – уравнениям, составленным по характеристикам, которые в данном случае совпадают с линиями скольжения:
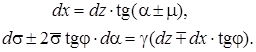 (2)
(2)
Здесь: ![]() – среднее приведенное напряжение; a – угол между направлением первым главным напряжением s1 и осью Ozm=p/4 -j/2 – угол между направлением s1 и линиями скольжения (рис. 2).
– среднее приведенное напряжение; a – угол между направлением первым главным напряжением s1 и осью Ozm=p/4 -j/2 – угол между направлением s1 и линиями скольжения (рис. 2).
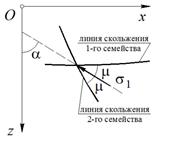
Рис. 2. Взаимная ориентация линий скольжения и направления s1
Верхние знаки в уравнениях (2) отвечают линиям скольжении 1-го семейства, нижние – 2-го семейства.
Решение для конкретных схем достигается численным интегрированием канонических уравнений (2) методом конечных разностей в рамках определенной последовательности краевых задач. Детально алгоритм численной реализации таких задач описан, например, в [4]. Рассчитав в каждой точке основания параметры канонической системы уравнений s и a, компоненты предельных напряжений определятся по формулам:
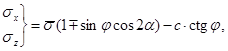
![]() .
.
Обратимся к расчетной схеме системы ленточных фундаментов, объединенных пологими оболочками (рис. 3). Данная задача обладает двумя особенностями:
-
ленточные фундаменты могут находиться достаточно близко друг к другу, и в этом случае необходимо строить поле предельных напряжений с учетом влияния соседних фундаментов;
-
выпуклое очертание границы основания между фундаментами требует задания специфических граничных условий.
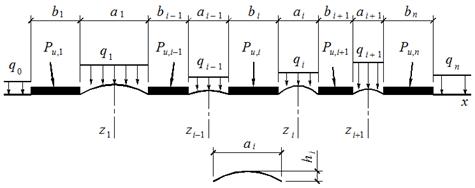
Рис. 3. Граничные условия к расчетной схеме фундаментов-оболочек в общем случае
Что касается первого замечания, то здесь будем придерживаться алгоритма, разработанного в [3] и в [8] для решения задач о близкорасположенных фундаментах. Отметим, что существуют работы, в которых рассматривается аналогичная проблема, но с несколько иных позиций [1, 6]. Что касается граничных условий на криволинейной поверхности под оболочками, то они приняты по следующей схеме: боковая пригрузка q=const на конкретном участке границы (рис. 3). При этом трение между оболочкой и грунтом не учитывается, следовательно, пригрузка q направлена по нормали к рассматриваемой поверхности.
Таким образом, величины боковых пригрузок qi считаются заданными; требуется определить величины предельных давлений по подошвам ленточных фундаментов pu,i.
Согласно алгоритму [3, 4] решения задач ТПРГ о несущей способности близкорасположенных фундаментов, расчетные схемы, аналогичные принятой к рассмотрению (рис. 3), можно разбить на n независимых схем, заключенных между вертикальными линиями, которые проходят через середины расстояний между штампами. Это осуществляется с помощью построения, представленного на рисунке 4, где римскими цифрами проставлены номера краевых задач.
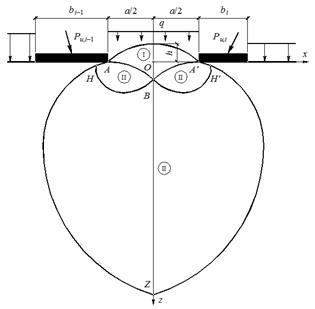
Рис. 4. Схема к дискретизации общей расчетной схемы
В зоне AA′B решается I краевая задача при указанных выше граничных условиях на криволинейной поверхности AA′. На полученных характеристиках AB и A′B и известных граничных условиях в особых точках A и A′(с учетом поправок, вносимых криволинейным очертанием границы AA′) решаются II краевые задачи в зонах радиального веера ABH и A′BH′. После этого на характеристиках BH и BH′, принадлежащих разным семействам, решается II краевая задача в области HBH′Z.
Основное содержание этого этапа решения состоит в том, что граничные условия правее точки A′ и левее точки A не оказывают влияния на построение решения в области AA′Z. Таким образом, на первом этапе определяются все параметры канонической системы уравнений (2) вдоль всех вертикальных линий, проходящих через середины расстояний между фундаментами, после чего эти линии фактически становятся границами для расчетной схемы i-го фундамента, как это показано на рисунке 5. На этом же рисунке римскими цифрами проставлены номера краевых задач.
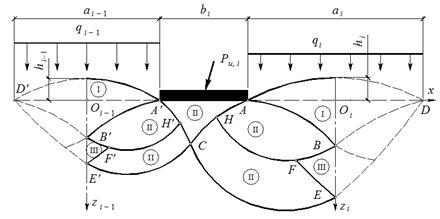
Рис. 5. Расчетная схема к построению решения в основании i-го фундамента
Более подробно последовательность решения этого класса задач описана в [4]. Здесь же отметим необходимость учета криволинейного очертания границы, что вносит определенные коррективы в построение конечно-разностной сетки линий скольжения и задание граничных условий как на криволинейных участках, так и в особых точках A¢ и A.
При определении полей статически безопасных напряжений для крайних фундаментов можно воспользоваться модификацией этой же расчетной схемы. Отличие будет состоять в том, что, с одной стороны, от рассматриваемого фундамента будет находиться оболочка и ограничивающая вертикальная линия (например, Oizi), а с другой – свободная горизонтальная поверхность.
Выводы
Получено новое статическое решение теории предельного равновесия грунтов и решена задача о несущей способности оснований ленточных фундаментов, объединенных пологими цилиндрическими оболочками (мембранами) для следующих случаев:
- Ленточный фундамент, объединенный с соседними ленточными фундаментами пологими оболочками, при достаточно большом удалении от соседних фундаментных лент;
- Промежуточный ленточный фундамент, объединенный с соседними ленточными фундаментами пологими оболочками, с учетом влияния соседних фундаментных лент на напряженное состояние основания;
- Крайний ленточный фундамент, объединенный с соседним ленточным фундаментом пологой оболочкой (мембраной), с учетом влияния соседней фундаментной ленты на напряженное состояние основания.
Рецензенты:
Чекардовский М.Н., д.т.н., профессор, заведующий кафедрой «Теплогазоснабжение и вентиляция» ФГБОУ ВПО ТюмГАСУ, г. Тюмень.
Соколов В.Г., д.т.н., профессор, профессор кафедры «Строительная механика», ФГБОУ ВПО ТюмГАСУ, г. Тюмень.
Библиографическая ссылка
Гербер А.Д., Пронозин Я.А., Епифанцева Л.Р. РАСЧЕТ ОСНОВАНИЙ ЛЕНТОЧНЫХ ФУНДАМЕНТОВ, ОБЪЕДИНЕННЫХ ОБОЛОЧКАМИ ИЛИ МЕМБРАНАМИ, ПО НЕСУЩЕЙ СПОСОБНОСТИ // Современные проблемы науки и образования. 2014. № 3. ;URL: https://science-education.ru/ru/article/view?id=13344 (дата обращения: 11.02.2026).



