Введение
При разработке устройств управления и обработки сигналов требуется соблюсти баланс между производительностью, энергопотреблением и габаритами системы. Особенно актуальным это становится при создании миниатюрных устройств, например, систем RFID, встраиваемых видео- и аудиосистем. Широкое применение в таких системах находят процессоры малой разрядности, использующие представление чисел с фиксированной точкой. В то же время рост частотного диапазона работы и быстродействия микропроцессоров предъявляет новые требования к математическому обеспечению, используемому для построения вычислительных моделей динамических систем.
Z-преобразование является стандартным и наиболее распространенным методом преобразования непрерывных моделей динамических систем в дискретные при реализации их средствами цифровой электроники. Однако у z-преобразования есть существенный недостаток: при стремлении периода дискретизации 
к нулю корни и полюса системы в z-области стремятся к единице [1]. При ограниченной точности машинного представления чисел различные корни стремятся «слиться» друг с другом и с единицей, и динамическая характеристика исходной цифровой системы может существенно отличаться от динамической характеристики непрерывной системы. Этот эффект можно уменьшить, если использовать представление чисел с плавающей точкой, однако на аппаратном уровне его поддерживает довольно ограниченное число контроллеров.
В то же время дельта-преобразование специально предназначено для того, чтобы устранить вышеописанный недостаток. При уменьшении периода дискретизации динамическая характеристика дельта-системы стремится к характеристике непрерывной. Но и дельта-преобразованию присущ недостаток: дельта-интегратор имеет неустойчивый полюс 
, что при определенных условиях приводит к падению точности модели. В данной статье рассматриваются условия возникновения неустойчивости и предлагается метод повышения точности дельта-преобразования.
Введение в дельта-преобразование
Разложим переменную 
в ряд Тейлора и сгруппируем его:
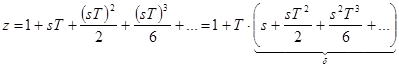(1)
При малых все члены ряда (1), начиная с 
, становятся много меньше единицы, и в числах с фиксированной запятой точность их представления оказывается неудовлетворительной. Основная идея Миддлтона и Гудвина [4] – использовать замену вида:
(2)
Это равносильно внесению первого члена ряда (2.1) – единицы – в коэффициенты передаточной функции, чтобы они более равномерно заполняли разрядную сетку [4]. Здесь 
– новая операторная переменная, которая вводится вместо 
. Формула (2) легко модифицируется:
(3)
где 
– параметр, обеспечивающий масштабирование коэффициентов дискретной модели от переменной .
Подстановка выражения (3) в преобразование Тастина дает:
, (4)
что позволяет строить дельта-модели на основе имеющихся непрерывных моделей. На практике удобнее сначала получить z-преобразование системы по Тастину, и только потом преобразовывать ее с помощью дельта-преобразования. При этом требуется соответствующий пересчет коэффициентов модели (описанный, например, в [1]).
Получив коэффициенты передаточной функции, требуется преобразовать вычислительную модель к виду кода, исполняемого на целевом устройстве. Каноническая форма (англ. directformII) имеет наименьший уровень шума квантования при реализации дельта-модели в арифметике с фиксированной запятой [3], а потому наиболее предпочтительна. В случае обычной дискретной канонической формы, когда используется оператор задержки 
, верно соотношение:
.
Передаточная функция дельта-интегратора выводится из (3):
. (5)
Для дельта-системы: 
, откуда, используя (5):
(6)
Тогда выражение для вычисления отклика дельта-системы в прямой форме 2 для звена 2-го порядка аналитически может быть записано:
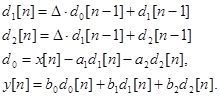(7)
Неустойчивость дельта-интегратора
Рассмотрим поведение переменных состояния 
дискретной модели ЛДС 2-го порядка, полученной с помощью дельта-преобразования. Введем функцию передачи 
. Непосредственно из (5) следует:
(8)
Дискретное звено второго порядка 
содержит неустойчивый полюс и является астатическим фильтром нижних частот. Это означает, что при низких частотах переменная состояния 
имеет величину много большую, чем 
, а при высоких частотах стремится к нулю и имеет величину много меньшую, чем . Переменная 
при этом занимает «промежуточное» положение.
Из структурной схемы канонической формы после подстановки выражения для 
может быть определена передаточная функция 
:
, (9)
где 
– коэффициенты знаменателя исходной передаточной функции от переменной . В свою очередь, (9) является фильтром верхних частот, при этом:
.
Частотные свойства переменной состояния определяются передаточной функцией 
, которая является дискретным фильтром нижних частот:
.
Таким образом, из свойств 
и 
следует, что переменные состояния дельта-модели являются ограниченными сверху. Однако они могут принимать очень малые значения, что в арифметике с фиксированной запятой приводит к повышению влияния шума квантования. Заметим, что использование транспонированной канонической формы не разрешает проблему неустойчивости дельта-интегратора.
Дельта-кси-преобразование
Введем следующую модификацию выражения (3):
,
где 
– некоторое малое число. Смысл введения 
– устранить корень . Введя обозначение 
, получим исходную формулу для дельта-кси-преобразования:
.
Здесь индекс 
при переменной 
введен для явного указания на то, что используется именно дельта-кси преобразование. Выражения для пересчета коэффициентов обычной дискретной модели в форме z-преобразования (полученной, например, с помощью преобразования Тастина) в коэффициенты дельта-кси-модели звена второго порядка приведены в таблице 1.
Таблица 1. Пересчет коэффициентов z-модели в коэффициенты дельта-кси-модели
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Оператор 
будет записан как:
. (10)
Формула (10) также является дискретным фильтром нижних частот, но теперь не астатическим. Легко показать, что
, (11)
то есть в области низких частот усиление уже не бесконечно велико. Функция передачи для дельта-кси-преобразования определяется как
. (12)
Выбор оптимального параметра 
может быть осуществлен из следующего условия: если 
, то в области нижних частот, вплоть до частоты среза дискретного ФНЧ (11), все переменные состояния будут иметь одинаковые амплитуды, и их значения заполнят практически всю разрядную сетку. Таким образом, шум квантования будет существенно снижен. Из (12) найдем выражение для расчета при условии, что в области нижних частот переменные состояния имеют одинаковую амплитуду:
.
Оно имеет единственное решение при дополнительном ограничении
:
. (13)
Окончательно, субоптимальное 
:
,
где – малое число для варьирования . Дело в том, что при реализации дельта-кси-преобразования в арифметике с фиксированной запятой требуется умножение на 
, что порождает дополнительный шум квантования. Действительно, выражения для вычисления отклика звена второго порядка в случае дельта-кси-преобразования:
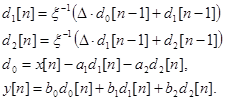(14)
Первые две строки модели (14) содержат умножение на , которое может быть выполнено точно, только если является степенью двойки. Однако в случае вычисления по формуле (13) это невозможно. Поэтому необходимо экспериментальное исследование дельта-кси-модели с коррекцией значения . Эксперименты показывают, что для достижения наилучших результатов коррекции должны подвергаться десятитысячные доли .
Выбор соответствующей амплитуды переменной состояния обеспечивается масштабированием входного сигнала по максимальному значению амплитуды этой переменной состояния, определенной передаточной функцией:
.
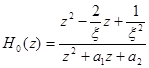Возьмем фильтр Бесселя нижних частот с частотой среза 50 Гц, заданный выражением в качестве эталонной непрерывной ЛДС, и примем период дискретизации 
мс. Для дельта-модели этого фильтра аплитудно-частотные характеристики функций передачи и 
представлены на рисунке 1.
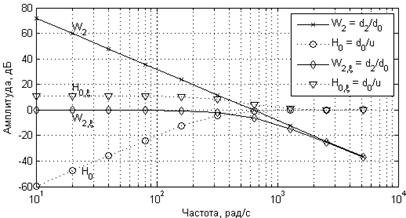
Рисунок 1. Амплитудно-частотные характеристики функций передачи и
Графики нам демонстрируют полученное выше качественное описание поведения переменных состояния для конкретного примера. Сравнение отклика дельта-модели и дельта-кси-модели представлено на рисунке 2.
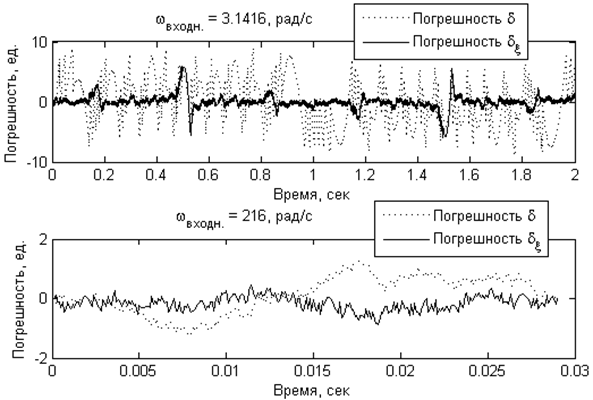
Рисунок 2. Сравнение отклика дельта-модели и дельта-кси-модели фильтра Бесселя
Сравнение показывает, что на малых частотах дельта-кси-преобразование обеспечивает существенно лучшую точность, чем дельта-преобразование, в то время как на больших частотах не хуже его и также может быть точнее. Так, в приведенном примере интеграл ошибки на частоте 3,14 рад/с дельта-модели в 26 раз больше, чем дельта-кси-модели, а СКО отклика – в 3,3 раза больше. На частоте 216 рад/с интегральные ошибки приблизительно равны, в то время как СКО отклика дельта-модели больше в 2,2 раза, чем дельта-кси-модели. При реализации на специальных вычислителях систем, которые должны иметь высокие точностные характеристики в области низких частот, такое улучшение существенно.
Заключение
В данной статье рассмотрено поведение переменных состояния дискретной модели звена второго порядка, полученной с помощью дельта-преобразования. Показано, что при реализации дельта-модели в канонической форме переменные состояния на разных частотах имеют различную амплитуду, что при реализации на специальных вычислителях при использовании арифметики с фиксированной точкой приводит к повышению шума квантования. Введено дельта-кси-преобразование, выравнивающее амплитуду переменных состояния в области нижних частот, что позволяет в этом частотном диапазоне уменьшить интеграл погрешности в десятки раз.
Работа выполнена в СПбГЭТУ при финансовой поддержке Министерства образования и науки Российской Федерации в рамках договора № 02.G25.31.0058 от 12.02.2013 г.
Рецензенты:
Авдеев Б.Я., д.т.н., профессор кафедры информационно-измерительных систем и технологий. Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина)», г. Санкт-Петербург.
Пузанков Д.В., д.т.н., профессор кафедры вычислительной техники. Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина)», г. Санкт-Петербург.
Библиографическая ссылка
Бутусов Д.Н., Каримов Т.И., Каримов А.И. ПРИМЕНЕНИЕ МОДИФИЦИРОВАННОГО ДЕЛЬТА-ПРЕОБРАЗОВАНИЯ ПРИ ПРОЕКТИРОВАНИИ СПЕЦИАЛИЗИРОВАННЫХ ВЫЧИСЛИТЕЛЕЙ // Современные проблемы науки и образования. – 2014. – № 3. ;URL: https://science-education.ru/ru/article/view?id=13330 (дата обращения: 20.04.2024).