В условиях модернизации современного российского высшего образования основным направлением его совершенствования является повышение качества обучения и контроля знаний [4, 6, 7, 9, 10].
В данной работе аналогично [1-3] проведен многомерный статистический анализ результатов оценивания знаний по высшей математике (выборка ЭНИН объема n =237) в объеме 1-го семестра (линейная алгебра и аналитическая геометрия + дифференциальное исчисление) студентов очной формы обучения Энергетического института Томского политехнического университета [8]. Рассмотрение проведено в системе 4-х показателей (рис.1): ВК – результаты тестового входного контроля по математике, АТТ1 – результаты текущей аттестации по высшей математике в середине семестра, АТТ2 – результаты текущей аттестации по высшей математике в конце семестра, ЭКЗ – результат классического экзамена.
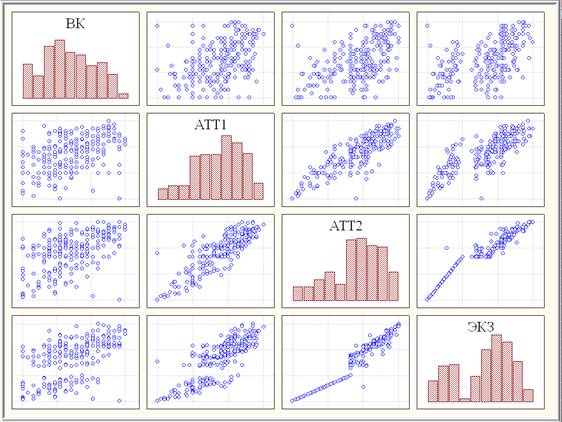
Рис. 1. Диаграммы рассеяния с гистограммами переменных выборки ЭНИН
Все числовые результаты ВТ приведены к единой 5-балльной шкале (делением результата на соответствующий максимальный результат и умножением на пять). Созданная таким образом в MS Excel база данных использовалась далее в пакете Statistica [5] для статистического анализа данных.
В рамках корреляционного анализа выявлены высоко значимые (на уровне значимости р < 0,0005) положительная корреляционная зависимость между АТТ1, АТТ2 и ЭКЗ (коэффициенты парных корреляции Пирсона r и Спирмена R > 0,81).
С учетом корреляционной зависимости исходных показателей (АТТ1, АТТ2 и ЭКЗ) на основании факторного анализа проведено сокращение их числа до двух (Ф1 и Ф2) и проведена интерпретация новых переменных по нагрузкам, характеризующим корреляции между факторами и показателями (табл. 1).
Таблица 1
Вращаемые факторные нагрузки в выбранной 2-х факторной модели ЭНИН
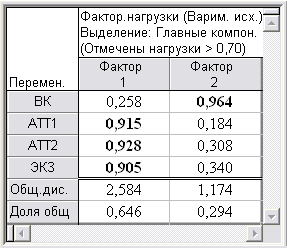
Согласно табл. 1, высокие факторные нагрузки исходных показателей распределились по факторам следующим образом:
Фактор ф1 – фактор текущей успеваемости {АТТ1+АТТ2+ЭКЗ} характеризуется положительной корреляционной связью.
Фактор ф2 – фактор ВК характеризуется положительной корреляционной связью.
Для проведения дальнейшего анализа ЭНИН в рамках построенной 2-х факторной модели вычислены значения наблюдений в новой системе факторных координат.
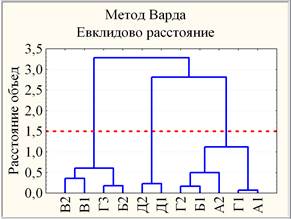
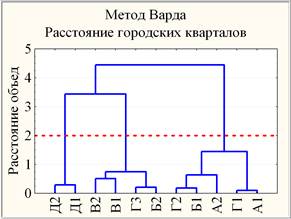
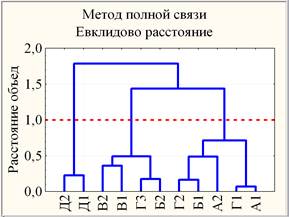
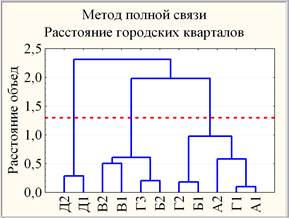
В построенном 2-х мерном факторном пространстве {ф1, ф2} проведена кластеризация 11-и учебных групп ЭНИН и построено иерархическое дерево (рис. 2).
|
|
|
|
|
|
Рис. 2. Дендрограммы наблюдений в пространстве {ф1, ф2}, построенные с использованием разных мер близости и правил объединения двух кластеров
В результате получено разбиение 11 групп на 3 кластера, обладающее устойчивостью относительно вариации мер близости (расстояние Евклида, Чебышева, городских кварталов) и правил объединения двух кластеров (метод Варда, полной связи, попарного среднего).
В построенном 2-х мерном факторном пространстве {ф1, ф2} методом K-средних, проводящим классификацию объектов по заданному количеству кластеров, получена также 3-х кластерная высококачественная модель результатов ЭНИН, распределяющая 11-и учебных групп студентов по 3-м кластерам высоко значимо (на уровне значимости р < 0,0005) согласно λ-критерию Уилкса по совокупности показателей ф1 и ф2 (рис.3).
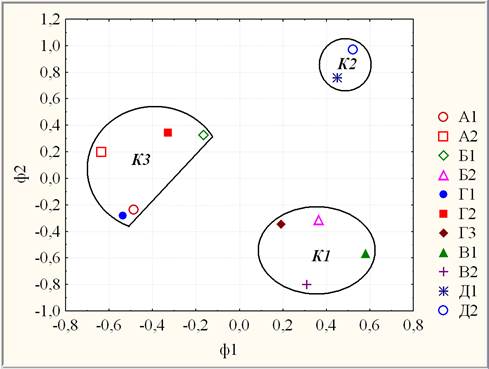
Рис. 3. Диаграмма рассеяния кластеров ЭНИН в факторных координат {ф1, ф2}
Алгоритм метода K-средних, перемещая объекты в разные кластеры с целью минимизации изменчивости внутри кластеров и максимизации изменчивости между кластерами, оценивает качество кластеризации наблюдений по каждому фактору посредством параметрического дисперсионного анализа (табл. 2).
Таблица 2
Результаты дисперсионного анализа кластеризации наблюдений по факторам ЭНИН
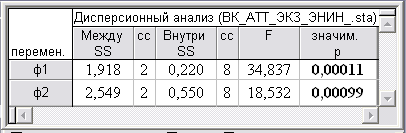
Согласно табл. 2, три кластера различаются высоко значимо по ф1 (на уровне значимости р »0,0001< 0,0005) и сильно значимо по ф2 (на уровне значимости 0,0005 < р »0,001< 0,005).
Кластерные средние по старым {ВК, АТТ1, АТТ2, ЭКЗ} и новым {ф1, ф2} показателям приведены в табл. 3.
Таблица 3
Кластерные средние m по ВК, АТТ1, АТТ2, ЭКЗ (5-ти балльная шкала), ф1, ф2 (стандартизированные)
|
Кластер |
АТТ1 |
АТТ2 |
ЭКЗ |
ф1 |
ф2 |
ВК |
Состав |
|
К3 |
2,528 |
2,614 |
2,265 |
-0,437 |
0,067 |
2,257 |
А1, А2, Б1, Г1, Г2 |
|
К1 |
3,253 |
3,298 |
2,885 |
0,358 |
-0,499 |
1,845 |
Б2, В1, В2, Г3 |
|
К2 |
3,538 |
3,983 |
3,715 |
0,484 |
0,859 |
3,469 |
Д1, Д2 |
Согласно апостериорным критериям (Фишера, Шеффе, Тьюки) можно оформить результаты множественных сравнений кластерных средних в порядке их убывания для каждого фактора:
ф1: {К1, К2}, {К3}, так, что К2 отличается от К3 высоко значимо (на уровне значимости р < 0,0005).
ф2: {К2}, {К3}, {К1} так, что К3 отличается как от К1, так и от К2 статистически значимо (на уровне значимости 0,005< р < 0,05).
Построенные последовательности неоднородных групп кластеров по каждому фактору находятся в согласии с результатами множественных сравнений по непараметрическому критерию Краскела – Уоллиса, смягчающему для ф1 отличие К2 от К3 до слабо значимого (на уровне значимости 0,05< р < 0,10), а для ф2 отличие К1 от К2 до статистически значимого (на уровне значимости 0,005< р < 0,05). При этом три кластера по совокупности различаются по каждому фактору статистически значимого (на уровне значимости 0,005< р < 0,05).
Графики кластерных средних для каждого фактора приведены на рис. 4.
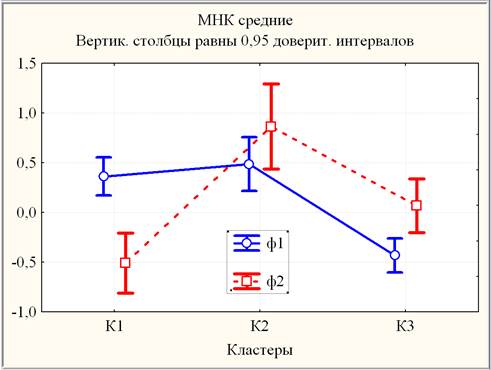
Рис. 4. Линейные графики факторных (стандартизированных) средних с 95 % границами доверительных интервалов для каждого кластера
Результаты кластерного анализа наблюдений по совокупности факторов с учетом результатов множественных сравнений кластерных средних для каждого фактора позволяют провести классификацию наблюдений в порядковой шкале стандартизированных измерений, полагая в качестве уровня «Средний» – стандартизированный интервал (-0,25; +0,25), «Выше среднего» – (+0,25; +1), «Ниже среднего» – (-1; -0,25).
Таблица 3
Классификация наблюдений по совокупности факторов в порядковой шкале стандартизированных измерений
|
Кластер |
Объем кластера |
ф1 {АТТ+ЭКЗ} |
ф2 {ВК} |
|
К1 |
4 |
Выше среднего |
Ниже среднего |
|
К2 |
2 |
Выше среднего |
Выше среднего |
|
К3 |
5 |
Ниже среднего |
Средний |
Согласно рис. 3–4 и табл. 3–4, две группы студентов (К2) демонстрируют стабильный уровень «Выше среднего» (mВК » 3,47 и mАТТ2 » 3,98), четыре группы (К1) – значимую положительную динамику (от mВК » 1,85 до mАТТ2 » 3,30) и пять групп – слабую динамику (от mВК » 2,26 до mАТТ2 » 2,61).
Выводы
-
В рамках корреляционного анализа выявлены высоко значимые (на уровне значимости р < 0,0005) положительная корреляционная зависимость между АТТ1, АТТ2 и ЭКЗ (коэффициенты парных корреляции Пирсона r и Спирмена R > 0,81).
-
С учетом корреляционной зависимости показателей на основании факторного анализа построены Ф1 – фактор текущей успеваемости {АТТ1+АТТ2+ЭКЗ} и Ф2 – фактор ВК.
-
В 2-х мерном факторном пространстве {Ф1, Ф2} методом K-средних получена 3-х кластерная значимая модель, распределяющая 11 групп студентов по 3-м кластерам.
-
В рамках дисперсионного анализа выделены для каждого фактора однородные (различающиеся незначимо) группы кластеров.
-
Проведена классификация результатов оценивания усвоенных студентом знаний по высшей математике в номинальной шкале измерений.
-
Результаты подобной кластеризации (по совокупности показателей) результатов оценивания знаний могут быть учтены в процессе обучения для оценки качества образования и контроля знаний.
Работа выполнена при поддержке Российского научного фонда.
Рецензенты:
Трифонов А.Ю., д.ф.-м.н., профессор кафедры высшей математики и математической физики, ФГБОУ ВПО «Национальный исследовательский Томский политехнический университет, г. Томск.
Арефьев К.П., д.ф.-м.н., профессор кафедры высшей математики, ФГБОУ ВПО «Национальный исследовательский Томский политехнический университет, г. Томск.
Библиографическая ссылка
Болтовский Д.В. ФАКТОРНЫЙ ПОДХОД КЛАСТЕРИЗАЦИИ РЕЗУЛЬТАТОВ ОЦЕНИВАНИЯ МАТЕМАТИЧЕСКИХ ЗНАНИЙ В СИСТЕМЕ ВЫСШЕГО ОБРАЗОВАНИЯ // Современные проблемы науки и образования. 2014. № 3. ;URL: https://science-education.ru/ru/article/view?id=13284 (дата обращения: 11.02.2026).