Введение
Конические оболочечные конструкции находят большое применение в ракетостроении, самолетостроении, судостроении, автомобилестроении и строительстве [7]. Для придания большей жесткости тонкостенная часть оболочки подкрепляется ребрами, при этом незначительное увеличение веса конструкции существенно повышает ее прочность, даже если ребра имеют малую высоту.
Подавляющее большинство работ, посвященных изучению динамики ребристых оболочек, выполнено с использованием расчетной схемы, основанной на прикладной теории оболочек Кирхгофа–Лява [2–4, 6, 9] и теории стержней Кирхгофа–Клебша. В некоторых работах использована теория оболочек типа Тимошенко, и лишь в работе [5] – уравнения пространственной задачи теории упругости. К сожалению, области применимости результатов, полученных на основе прикладных теорий, в большинстве случаев не оговариваются, и вопрос о достоверности результатов, полученных с помощью этих теорий, в особенности при решении нестационарных задач, остается открытым.
В наиболее общем виде построены уравнения движения ребристых цилиндрических оболочек [1, 8].
В работах [11, 12] были получены уравнения движения для подкрепленных ребрами жесткости конических оболочек при линейно-упругом деформировании с учетом поперечных сдвигов. Однако при исследовании устойчивости оболочек в динамической постановке при нагрузках, близких к критическим, могут проявиться пластические деформации.
Цель исследования
Разработка математической модели деформирования конических оболочек с учетом геометрической и физической нелинейности при динамическом нагружении.
Материал и методы исследования
Будем рассматривать математические модели классической теории оболочек, основанной на определенных гипотезах (существуют и другие теории оболочек, например, асимптотическая).
Полная совокупность соотношений, характеризующих деформирование оболочек, состоит из трех групп. К первой группе относятся соотношения между деформациями и перемещениями оболочки (геометрические соотношения). Эти соотношения зависят от геометрии оболочек (цилиндрические, конические, сферические и т. д.). Если допускаются малые перемещения, то эти соотношения линейные. Если оболочка допускает прогибы, соизмеримые с ее толщиной, то эти соотношения нелинейные. Таким образом, учитывается геометрическая нелинейность. Ко второй группе относятся соотношения, связывающие напряжения и деформации (физические соотношения). Эти соотношения зависят от того, какие свойства материала конструкции учитываются (упругие, пластические, свойства ползучести и т. д.). Проявление тех или иных свойств материала зависит от уровня внешних воздействий и их длительности. К третьей группе относятся уравнения равновесия (движения) или функционал полной энергии деформации, который представляет сумму работ внутренних и внешних сил и из условия минимума которого получаются уравнения равновесия (движения). Все эти зависимости вместе с краевыми условиями (условиями закрепления краев оболочки) образуют замкнутую систему, в которой число неизвестных равно числу уравнений, и составляют математическую модель деформирования оболочки.
Для круговой конической оболочки с углом конусности q параметры Ляме принимают вид ![]() , кривизны –
, кривизны – ![]()
![]() , так как
, так как ![]()
![]()
![]() . Принимаемая система координат показана на рис. 1.
. Принимаемая система координат показана на рис. 1.
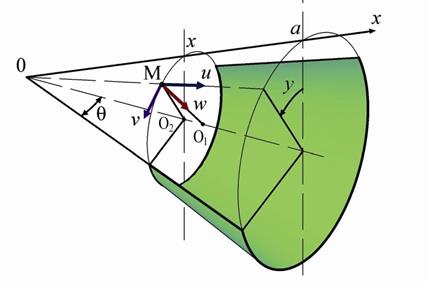
Рис. 1. Круговая коническая оболочка
Деформации в срединной (координатной) поверхности принимают вид:
![]()
![]()
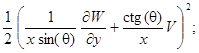 (1)
(1)
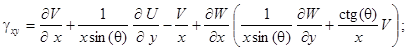
![]()
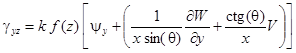 .
.
Функции изменения кривизн ![]() и кручения
и кручения ![]() принимают вид:
принимают вид:
![]()
![]()
Выражения ![]() здесь принимают вид:
здесь принимают вид:
![]()
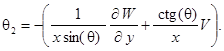
Физические соотношения (связь напряжений и деформаций) для упругого изотропного материала оболочки будут иметь вид:
![]()
![]() (2)
(2)
![]()
Таким образом, физические соотношения для изотропного материала принимают вид:
![]()
![]() (3)
(3)
![]()
![]()
Для учета пластических деформаций будем использовать деформационную теорию пластичности, при этом секущий модуль упругости принимаем в виде, предложенном А. А. Ильюшиным:
![]() .
.
Таким образом, физические соотношения могут быть записаны в виде:
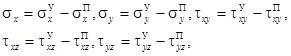
где ![]() ,
, ![]() ,
,![]() ,
, ![]() ,
, ![]() имеют вид (3), а составляющие напряжений
имеют вид (3), а составляющие напряжений ![]() записываются в виде:
записываются в виде:
![]()
![]() (4)
(4)
![]()
![]()
![]()
При использовании для решения физически-нелинейных задач метода упругих решений А.А. Ильюшина на каждой итерации ![]() считается известной величиной.
считается известной величиной.
Функция ![]() для различных материалов принимает различный вид, а
для различных материалов принимает различный вид, а ![]() имеет вид:
имеет вид:
![]()
Будем считать, что на оболочку действует поперечная нагрузка ![]() . Значит, искомые функции перемещений
. Значит, искомые функции перемещений ![]() и углов поворота нормали
и углов поворота нормали ![]() будут функциями трех переменных
будут функциями трех переменных ![]() ,
, ![]() и
и ![]() .
.
Функционал полной энергии деформации оболочки имеет вид:
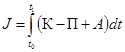 , (5)
, (5)
где ![]() – кинетическая энергия системы,
– кинетическая энергия системы, ![]() – потенциальная энергия системы,
– потенциальная энергия системы, ![]() – работа внешних сил. При учете физической нелинейности потенциальная энергия системы будет иметь вид [12]:
– работа внешних сил. При учете физической нелинейности потенциальная энергия системы будет иметь вид [12]:
![]() .
.
В функционале (5)
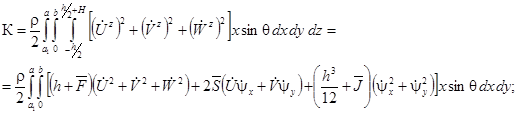 (6)
(6)
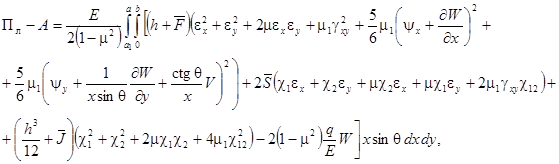 (7)
(7)
где ![]() .
.
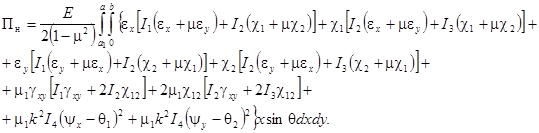 (8)
(8)
В выражении (6), ![]() – плотность материала оболочки, точками обозначены производные по переменной
– плотность материала оболочки, точками обозначены производные по переменной ![]() .
.
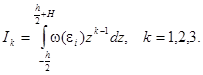
Для разных материалов используют различную аппроксимацию ![]() , например,
, например,
![]()
![]()
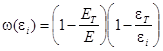 при
при ![]() (
(![]() при
при ![]() )
)
и другие. Аппроксимация секущего модуля ![]() может быть использована, например, для таких материалов, как сталь ХГ, сталь Р9, сплав 765.
может быть использована, например, для таких материалов, как сталь ХГ, сталь Р9, сплав 765.
Высота и расположение ребер задается функцией:
![]()
где ![]() - высота ребер параллельных осям
- высота ребер параллельных осям ![]() и
и ![]() соответственно;
соответственно; ![]() ;
; ![]() ,
, ![]() - единичные столбчатые функции, равные единице в местах присоединения ребер и равные нулю вне таких мест. Контакт ребра и обшивки происходит по полосе.
- единичные столбчатые функции, равные единице в местах присоединения ребер и равные нулю вне таких мест. Контакт ребра и обшивки происходит по полосе.
Таким образом, толщина всей конструкции равна ![]() . Если
. Если ![]() , то оболочка подкреплена ребрами или накладками, а если
, то оболочка подкреплена ребрами или накладками, а если ![]() , то она ослаблена вырезами;
, то она ослаблена вырезами;
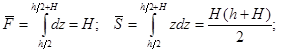
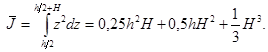
Выражение для ![]() представим в виде:
представим в виде:
![]() ,
,
где
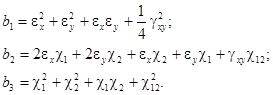
Так как
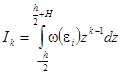 ,
,
то
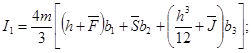
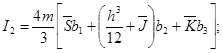
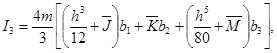
Для металла, не имеющего площадки текучести, ![]() принимает значение от
принимает значение от ![]() до
до ![]() и вычисляется эмпирически.
и вычисляется эмпирически.
Заключение
Функционал (5), с учетом (6), (7), (8), вместе с краевыми и начальными условиями представляет собой математическую модель деформирования конической оболочки при динамическом нагружении, в которой учитывается геометрическая и физическая нелинейности, дискретное введение ребер с учетом их сдвиговой и крутильной жесткости, а также поперечных сдвигов.
Панели усеченных конических оболочек зачастую используются в машиностроении, самолетостроении, автомобилестроении [7], при этом на конструкцию действуют именно динамические нагрузки. Полученная математическая модель позволяет исследовать не только напряженно-деформированное состояние конических оболочек, но и свободные и вынужденные колебания.
Рецензенты:
Ушаков А.И., д.т.н., профессор научно-производственного информационно-консультационного центра – плюс, г. Санкт-Петербург.
Максимов С.Е., д.т.н., профессор, генеральный директор научно-производственной компании «НТМТ», Ленинградская обл., г. Гатчина.
Библиографическая ссылка
Овчаров А.А., Брылев И.С. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДЕФОРМИРОВАНИЯ НЕЛИНЕЙНО УПРУГИХ ПОДКРЕПЛЕННЫХ КОНИЧЕСКИХ ОБОЛОЧЕК ПРИ ДИНАМИЧЕСКОМ НАГРУЖЕНИИ // Современные проблемы науки и образования. 2014. № 3. ;URL: https://science-education.ru/ru/article/view?id=13235 (дата обращения: 13.10.2025).



