В последнее время проблемная область управления проектами получила широкое развитие в связи с явной ориентированностью на решение прикладных задач бизнеса и промышленности. Менеджеры и руководители различных уровней успешно используют в своей практической деятельности инструментарий и методологию управления проектами для достижения максимального качества выпускаемого продукта при наличии строгих ресурсных ограничений. Такие параметры, как качество результатов, стоимость и сроки исполняемых контрактных работ, приобретают критическую актуальность и значимость особенно при использовании методов управления проектами и в связи с острыми проблемами взаимодействия в конкурентной среде.
Зачастую в сфере управления проектами визуальная модель сложной системы (а именно проекта) в форме сетевой либо линейной диаграммы [11-13] является одним из немногих способов принятия единственно правильного решения, от результатов которого будет зависеть успех высокотехнологичного бизнеса.
Проект, по нашему мнению, обладает явно выраженными системными свойствами [11-13], являясь большой и сложной системой. Большой - по причине размерности и крупномасштабности решаемых при помощи проектного подхода задач. Сложность проекта обуславливается разнообразием связей между структурными единицами проекта, а также синергетическими эффектами, возникающими в течение всего жизненного цикла. Поскольку проект является также развивающимся объектом [11-13], его состояния динамически изменяются, что может приводить к пересмотру сроков, стоимости и объемов работ, распределения ресурсов, возникновению разнородных рисков. Подойти обоснованно и взвешенно к управлению сложной и крупномасштабной системой затруднительно без специально разработанных эффективных визуальных представлений и разрезов графического анализа проблемной ситуации, которыми будет пользоваться лицо, принимающее решение, - менеджер проекта. Наиболее часто используемыми методами визуального анализа, применяемыми для структурирования сложных систем, являются модели теории графов [2; 11; 13; 18], которые также интенсивно используются в проектном менеджменте.
В статье предлагается использование оригинального программного инструментария планирования и управления проектами на основе графических методов анализа.
Комплекс методов и задач управления проектами
Согласно своду знаний по управлению проектами [10], предметная область проектного менеджмента включает в себя ряд задач, имеющих важное теоретическое и практическое значение, к числу которых относятся:
- управление интеграцией проекта;
- управление содержанием проекта;
- управление сроками проекта;
- управление стоимостью проекта;
- управление качеством проекта;
- управление человеческими ресурсами проекта;
- управление коммуникациями проекта;
- управление рисками проекта;
- управление поставками проекта.
Рассмотрим способы визуального представления проекта [14], составляющие системное описание объекта анализа. Несмотря на разнообразие задач в сфере управления проектами, визуальные модели и их представления опираются в основном на теорию графов.
Построение визуальной аналитической модели позволяет во многих случаях существенно сократить время решения поставленной задачи, подготовить обоснованное ее решение при помощи соответствующего программно-аналитического инструментария визуализации.
В настоящее время наиболее продвинутыми способами визуализации задач в области управления проектами являются корпоративные системы управления проектами, однако даже самый развитый программный инструментарий менеджера проектов не может в полном объеме решить задачи, связанные с визуально-аналитическим решением разнородных и разноплановых проблем в управлении проектами.
В современных условиях флагманские системы управления проектами конкурируют за наиболее качественное и оперативное визуальное информирование пользователей, а также представление визуальных результатов анализа с целью оперативного управления и вмешательства в управленческую ситуацию.
Следует отметить, что был разработан ряд локализованных стандартов в области управления проектами, которые успешно применяются в соответствующих регионах, например Prince2 - Великобритания, V-Model - Германия, Hermes method - Швейцария, ANCSPM - Австралия, P2M (Project and Program Management for Enterprise Innovation) - Япония, НТК - Россия. Используются также стандарты управления проектами с расширенной географией применения, например ISO 10006:2003, Quality management systems - Guidelines for quality management in projects.
Применение визуальной аналитики часто используется и при планировании и управлении ИТ-проектами, отличающимися высоким уровнем риска и изменчивостью; также актуальной задачей в области визуализации является портфельное и мультипроектное управление, учитывающее взаимозависимости между операциями и ресурсами, совместно используемыми несколькими проектами.
Первой стадией визуального моделирования состава проекта в соответствии с [14] является графическая древовидная модель иерархической структурной декомпозиции комплекса работ - иерархическая структура работ ИСР - WBS (Work Breakdown Structure), представляющая собой основу для дальнейшей разработки сетевой или линейной диаграммы. Проект на данной диаграмме визуально разбивается на ряд соподчиненных подзадач или операций в зависимости от уровня декомпозиции, выбранного менеджером.
По мере развития методов проектного менеджмента было разработано значительное разнообразие графических моделей, однако в настоящее время интенсивно используются сетевая и линейная модели, которые преобразуются одна в другую и позволяют переходить от одной формы представления к другой. Исторически линейная модель, или диаграмма Гантта, была предложена ранее сетевой модели комплекса работ. Рассмотрим примеры визуального представления различного вида сетевых моделей комплексов работ. Как известно [11-13], различают сетевые модели, в вершинах которых располагаются события (action on node), а также сетевые модели, в вершинах которых расположены операции (activity on arc). Данные сетевые модели типологически оказываются изоморфными, т.е. форма одной переходит в форму другой, на рис. 1 изображены сетевые модели, типологически изоморфные друг другу. Общепринятым является также способ представления комплексов работ проекта в виде линейных или ленточных диаграмм Гантта. На диаграмме Гантта отображаются временные параметры операций, отношения между работами, а также критические операции.
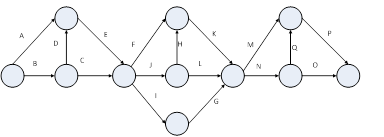
Рис. 1а. Сетевая модель, в вершинах расположены события.
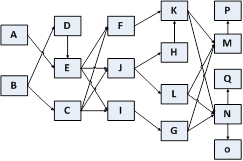
Рис. 1б. Сетевая модель, в вершинах расположены операции.
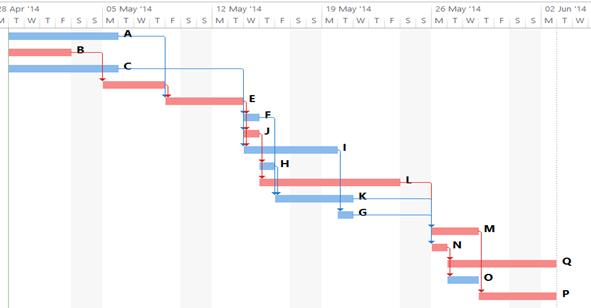
Рис. 1в. Линейная диаграмма Гантта с указанием сроков выполнения работ, связей и критических операций проекта.
Относительно способов визуализации комплексов работ проекта, достоинств и недостатков каждого из методов графического отображения можно отметить следующее.
- Сетевая и линейная модели проекта обе в достаточной степени отражают состав комплекса работ.
- Сетевая модель отражает взаимозависимости между операциями более четко, чем линейная модель с топологической точки зрения.
- Преимуществом сетевой модели перед линейной является то, что она более адаптирована для внесения изменений, постоянно возникающих в ходе реализации, планирования и управления проектами.
- При помощи сетевой модели может быть определена технологическая последовательность тех операций, которые входят в критический путь и определяют максимальные сроки реализации проектных работ.
- В то же время линейная модель проекта позволяет отслеживать сроки выполнения операций и визуально контролировать резервы некритических работ.
Календарное планирование прерываемых и непрерываемых работ проекта на основе разработанного программного продукта
Календарное планирование прерываемых и непрерываемых операций комплекса работ проекта является базовой задачей проектного менеджмента. С этой целью используется ряд эвристических и точных алгоритмов планирования [12], принимающих во внимание экзогенные и эндогенные параметры проекта.
Планирование проекта с учетом ресурсов производится с использованием Web-ориентированной системы, позволяющей производить составление календарного плана комплекса работ проекта при помощи присвоения приоритетов операциям. Приоритеты присваиваются операциям пользователем системы, причем необходимо ввести параметры длительности операций, индикатор прерываемости работы, а также количество ресурсов, потребляемых каждой работой.
После ввода исходных параметров выполняется отображение структуры комплекса работ проекта в виде сетевой модели и линейной диаграммы Гантта.
Решение задачи календарного ресурсного планирования комплекса работ выполняется в итерационном режиме в формате представления визуального пошагового решения задачи с использованием комплекса программных средств [6] на Web-ориентированной основе, разработанной автором.
Результат календарного планирования комплекса работ проекта в результате решения последовательным методом (в случает непрерываемых работ) и в случае решения задачи параллельным методом (для прерываемых операций) представляется в формате ресурсной и линейной диаграмм, учитывающих прерывания, возникающие в ходе выполнения работ.
Визуальное обучение основам календарного ресурсного планирования проектов осуществляется в обучающем режиме программного тренажера, разработанного автором [6]. Ознакомиться с визуальным тренажером, предназначенным для решения задач календарного планирования проектов, можно, проследовав по следующей ссылке (http://www.pressybutton.ru/).
Объединение и укрупнение комплекса работ проекта. Модель жизненного цикла на основе графов специального вида
Топологические преобразования комплекса работ проекта выполняются при помощи набора базовых процедур, основанных на последовательном и параллельном объединении сетевых моделей проектов, а также укрупнении и разукрупнении комплексов работ [11-13].
Результатом объединения частных сетевых фрагментов является сводная сетевая модель проекта.
Следует также отметить, что процедура разукрупнения (декомпозиции) сетевой модели комплекса работ выполняется, в основном опираясь на визуальное представление декомпозируемых частей графа. Декомпозицию сетевой модели комплекса работ можно выполнять путем приведения ее к виду, позволяющему производить обработку и анализ проекта по частям, добиваясь, таким образом, снижения размерности решаемой задачи.
Представляет определенный интерес изучение сетевой модели жизненного цикла проекта, которая позволяет обоснованно подойти к задаче управления с использованием визуального структурного представления в виде графа специального вида.
Вариант структуры жизненного цикла изделия в виде сетевой модели может быть разработан с использованием разработанного автором программного средства анализа жизненного цикла [3]. Согласно [16; 20] модель жизненного цикла имеет наглядную визуальную интерпретацию в терминах основных и вспомогательных процессов, входящих в его состав. Дуги, соединяющие несмежные вершины ориентированного графа интерпретируются как вспомогательные и обеспечивающие процессы жизненного цикла, а соединяющие смежные вершины графа - как основные процессы.
Модель жизненного цикла продукта имеет специфическую цепочечную структуру, позволяющую сформулировать ряд важных и практически значимых свойств [9; 10], особенно ориентируясь на визуальное представление [17].
Задачей, допускающей наглядную визуальную интерпретацию и анализ, является укрупнение[11; 13; 17] или агрегирование комплекса работ проекта, подразумевающее графическое отображение кумулятивной информации, касающейся временных и стоимостных параметров проекта. На различных уровнях управления задействованы специалисты, руководители, менеджеры, рядовые исполнители, решающие соответствующие выбранному уровню задачи. Специалисты пользуются на каждом уровне агрегированной или укрупненной информацией, уровень детализации которой убывает по мере продвижения вверх по организационной структуре управления, решая задачи, соответствующие определенному уровню информированности и компетентности.
В случае с цепочечным графом специальной структуры [10] известны процедуры эквивалентного по времени и стоимости укрупнения комплекса работ проекта [17], имеющие наглядное визуальное отображение. Руководство компанией на верхних уровнях управления чаще всего пользуется цепочечной структурой проекта, соответствующей жизненному циклу изделия, при помощи которой возможно эффективно решить управленческие задачи, опираясь на эквивалентное по времени и стоимости укрупнение комплекса работ. Следует заметить, что укрупнение сетевой модели комплекса работ осуществляется на основе выбранного менеджером подграфа или ключевых событий, подобных «остовным» [10; 17] событиям комплекса работ.
Укрупнение по событиям жизненного цикла [9] позволяет получить эквивалентное по времени и стоимости преобразование сетевой модели по выбранному подпроекту в составе комплекса работ.
Случаи укрупнения сетевых моделей, эквивалентного по стоимости и времени, возникающие в задачах параллельного объединения частных сетевых фрагментов, содержащих сопряженные операции [9], часто используются в задачах проектного менеджмента.
Так, укрупненные дуги сетевой модели комплекса работ имеют наглядную графическую и содержательную интерпретацию [17]. При укрупнении сетевых фрагментов (по выделенному подграфу), содержащих сопряженные операции, выделяются граничные события и внутренние события. В задаче укрупнения внутренние события удаляются, а граничные соединяются путями максимальной длины. Обозначим при помощи x1 - граничное событие укрупняемого частного сетевого подграфа, тогда определение временных параметров укрупненных операций не представляет затруднений, тогда как стоимостные параметры работ определяются исходя из следующих соотношений:
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
Следовательно, стоимости работ в укрупненном графе G0 в общем виде могут быть представлены следующими соотношениями:
![]() (4)
(4)
![]() (5)
(5)
![]() (6)
(6)
где ![]() ,
, ![]() ,
, ![]() - стоимость работ соответственно предшествующих, следующих за и несравнимых с событием x1.
- стоимость работ соответственно предшествующих, следующих за и несравнимых с событием x1.
Укрупненный граф, эквивалентный по времени и стоимости исходному, имеет цепочечную структуру, характерную для моделей полного жизненного цикла, используемых на уровне топ-менеджмента при принятии управленческих решений в компании.
Автором разработана программная система [3], решающая задачи визуального анализа процессов жизненного цикла продукции при помощи представления жизненного цикла продукции в виде специального графа цепочечного вида.
Программное средство для решения задач визуального анализа проектов позволяет также выполнить и ресурсное планирование комплекса работ, с учетом ограничений на доступное количество ресурсов.
Ресурсное планирование проектов
Известны эвристические и точные методы [18] аналитического решения задачи распределения ограниченных ресурсов между работами, входящими в состав комплекса операций сетевой модели проекта. Эвристические алгоритмы предоставляют приближенный ресурсно допустимый календарный план проекта, в то время как точные методы обеспечивают решение, являющееся результатом оптимизационного поиска альтернатив. Визуальная интерпретация полученных решений заключается в построении линейной диаграммы Гантта, совмещенной с ресурсным профилем проекта, посредством которых можно установить мажорируется ли ресурсный профиль сверху ограничением на доступное количество ресурсов, обеспечивается ли равномерность потребления ресурсов в проектах.
Для решения задач ресурсного планирования проектов и визуальной интерпретации полученных результатов автором был разработан набор программных систем, позволяющих выполнять анализ и планирование проектов по временным, стоимостным и ресурсным параметрам [1; 3-8].
Решение задачи ресурсного планирования комплекса работ проекта подразумевает [12] построение множества логически и ресурсно допустимых фронтов комплекса работ, допускающих эффективное визуальное представление в виде графа отношения несравнимости, позволяющего графически синтезировать множество полных фронтов.
При решении задачи ресурсного планирования используется также граф расстояний, применяемый для визуального решения задачи перехода между фронтами комплекса работ при минимальном количестве прерываний между операциями, входящими в состав проекта.
Над дугами графа, визуализирующего матрицу расстояний, применяемой для решений задачи ресурсного планирования проекта точным методом, изображены расстояния между фронтами работ, равные количеству различных операций, входящих в оба фронта. Расстояние при переходе от фронта Fi к Fj обозначено при помощи αij, расстояние при переходе от Fj к Fi - обозначается через βji, при невозможности перехода между фронтами комплекса работ в качества параметра перехода дуги графа используется символ ∞.
Кроме этого, возможно также произвести визуализацию процесса изменения затрат в ходе выполнения проекта при помощи пакета прикладных программ, разработанного автором [1].
Оперативное планирование и управление проектом
Наиболее эффективным инструментом, используемым на стадии оперативного планирования и управления, является метод освоенного объема [14], реализованный в ряде современных систем управления проектами. Вводится понятие плановых, фактических и освоенных затрат. Динамика их освоения отображается визуально при помощи техники специальных диаграмм, позволяющих выполнить анализ и прогнозирование результатов проекта в зависимости от реализующихся сценариев выполнения комплексов работ. Следует отметить, что данный инструментарий является незаменимым помощником менеджеров для решения задач контролирования проекта по стоимостным и временным параметрам.
Типичные формы визуального представления показателей освоенного объема позволяют отобразить динамику освоенных затрат и оценить перспективы реализации проекта в установленный директивный или критический сроки.
Значения планового объема, освоенного объема и фактической стоимости используются для определения измерения эффективности, а также для определения, выполнена или нет работа в плановом порядке и в предусмотренные планом сроки. Наиболее широко используемыми показателями являются отклонение по стоимости и отклонение по срокам. По мере приближения проекта к завершению величины отклонений по стоимости и по срокам снижаются. Это объясняется компенсационным эффектом, вызванным тем, что к этому времени большее количество работ оказываются выполненными. В плане управления стоимостью можно указать заранее установленные допустимые значения отклонений, которые будут снижаться по мере приближения проекта к окончанию. Построенные выше кривые позволяют проводить визуальный анализ освоенных затрат с учетом сказанного выше достаточно эффективно. Оценки временных параметров хода реализации проектов оцениваются в основном визуально. В оценке эффективности реализации проекта при помощи метода освоенного объема используются следующие показатели: ![]() – планируемая динамика затрат (БСЗР; в конкретный момент времени t – плановая суммарная стоимость работ, запланированных к выполнению за рассматриваемый период времени); C0 – планируемые суммарные затраты на проект (БПЗ – бюджет по завершении); c(t) – фактическая динамика затрат (ФСВР; в конкретный момент времени t – фактическая стоимость выполненных работ); cе(t) – динамика освоенных затрат (БСВР; в конкретный момент времени t – плановая стоимость выполненных работ); С – фактические суммарные затраты на проект. Следует отметить, что величины
– планируемая динамика затрат (БСЗР; в конкретный момент времени t – плановая суммарная стоимость работ, запланированных к выполнению за рассматриваемый период времени); C0 – планируемые суммарные затраты на проект (БПЗ – бюджет по завершении); c(t) – фактическая динамика затрат (ФСВР; в конкретный момент времени t – фактическая стоимость выполненных работ); cе(t) – динамика освоенных затрат (БСВР; в конкретный момент времени t – плановая стоимость выполненных работ); С – фактические суммарные затраты на проект. Следует отметить, что величины ![]() ,
, ![]() являются плановыми (т.е. известны руководству проекта), а величина
являются плановыми (т.е. известны руководству проекта), а величина ![]() , как правило, «ненаблюдаема», и для ее оценки используются процедуры, включающие сообщение информации от более информированных участников проекта менее информированным. На рис. 2 приведены показатели динамики основанных затрат по проекту, отображенные в графическом виде, удобном для визуального анализа.
, как правило, «ненаблюдаема», и для ее оценки используются процедуры, включающие сообщение информации от более информированных участников проекта менее информированным. На рис. 2 приведены показатели динамики основанных затрат по проекту, отображенные в графическом виде, удобном для визуального анализа.
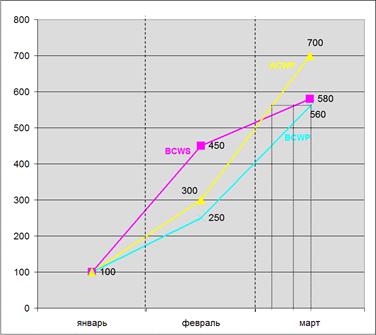
Рис. 2. Показатели освоенных затрат по проекту.
На рис. 2 использованы следующие показатели освоенного объема: BCWS - Budgeted Cost of Work Scheduled, ACWP - Actual Cost of Work Performed, BCWP - Budgeted Cost of Work Performed или EV - Earned Value.
Инвестиционно-финансовое планирование проекта
Рассмотрим подход к оценке экономического эффекта проекта, являющийся основой анализа финансовой осуществимости и опирающийся на структуризацию комплекса работ сетевой модели и последующий учет взаимосвязей этапов. Структура чистого приведенного дохода по проекту с учетом свойств жизненного цикла (ЖЦ) принимает следующий вид:
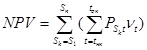 , (7)
, (7)
где s1,s2,..sn – стадии ЖЦ продукции, входящие в полный ЖЦ, tнк и tок – моменты начала и окончания соответствующей стадии Sk , Pt – величина дохода за соответствующий временной интервал t, νt – коэффициент дисконтирования, приводящий к сопоставимому виду разновременные потоки платежей. При необходимости в величину νt может быть введена «поправка на риск», а также и ожидаемый уровень инфляции.
В некоторых случаях оказывается возможным поставить в соответствие каждой работе свой поток доходов и расходов (затрат и эффекта). Тогда в наиболее общем виде выражение для NPV преобразуется к виду:
![]() (8)
(8)
В последнем случае сумма рассчитывается по всем работам u, входящим в комплекс работ U, ![]() - поток доходов, ассоциируемый с работой u комплекса в момент времени t,
- поток доходов, ассоциируемый с работой u комплекса в момент времени t, ![]() - поток расходов, ассоциируемый с работой u комплекса работ в момент времени t, а
- поток расходов, ассоциируемый с работой u комплекса работ в момент времени t, а ![]() - доход, эмерджентно возникающий при реализации события x в момент времени t.
- доход, эмерджентно возникающий при реализации события x в момент времени t.
Эффективным инструментарием стратегического инвестиционного и финансового планирования является технология визуального составления дорожных карт инновационных проектов. Как известно [21], дорожная карта является эффективным инструментом бизнес-прогнозирования инновационных целей и задач, который позволяет оценить уровень научно-технического прогресса в той или иной области исследований.
Также очевиден эффект использования дорожных карт в сфере визуализации результатов высокотехнологичных проектов в различных предметных областях.
Визуализация будущих результатов высокотехнологичного бизнеса в формате дорожных карт позволяет осознанно подойти к задачам отбора перспективных инновационных проектов с целью их последующей коммерциализации, комбинации эффекта от внедрения и долгосрочного финансирования. Пример дорожной карты инновационого проекта по созданию технологии производства алюминий-матричного нанокомпозитного материала приведен на рис. 3.
На основе разработанных дорожных карт (road maps) выполняется дальнейшее перспективное стоимостное, ресурсное и финансовое планирование будущих результатов инновационных проектов. Основными критериями оценки финансовых результатов, согласно технологии UNIDO [15], являются интегральные финансовые показатели, к числу которых относятся NPV, IRR, PI, DPB, MIRR.
Для визуализации интегральных финансовых показателей эффективности проектной деятельности используется ряд диаграмм, например чистого приведенного дохода, являющихся эффективным инструментом принятия инвестиционных решений и оценки окупаемости вложенных в проект средств.
Очевидным достоинством дорожной карты является возможность ее преобразования в линейную диаграмму Гантта и в дальнейшем использование последней при решении задач управления перспективным проектом реализации новшества [8]. Автором было разработано программное средство, позволяющее вести оценку перспективности вариантов реализации проектов на основе модели дорожной карты стратегического планирования бизнеса. Ознакомиться с интерактивной версией автоматизированной системы оценки бизнес-проектов можно, нажав на ссылку.
По нашему мнению, применение технологии дорожных карт является весьма перспективным в сочетании с методами управления проектами, направленными на достижения максимального качества при заданных ограничениях на ресурсы и бюджет. Дорожные карты реализуют системный подход к планированию и описанию бизнеса и содержат такие компоненты, как рыночные позиции проекта, описание продукта и технологии, проекты НИОКР и ресурсы, необходимые для реализации.

Рис. 3. Дорожная карта инновационного проекта.
При помощи аналитической системы Project Expert [13] оказывается возможным разработать комплексную имитационную финансовую модель инвестиционного проекта, позволяющую оценить эффект от его реализации, а также выполнить визуальный анализ хода реализации проекта. Календарный план проекта может быть визуализирован при помощи линейной диаграммы Гантта, также необходимо ввести параметры дохода и затрат по проекту, план по персоналу, источники финансирования проекта и выполнить расчет интегральных показателей эффективности.
Далее представлен график чистого приведенного дохода по проекту, отражающий процесс окупаемости инвестиций и интегральный эффект проекта в рублях в зависимости от времени, рис. 4.
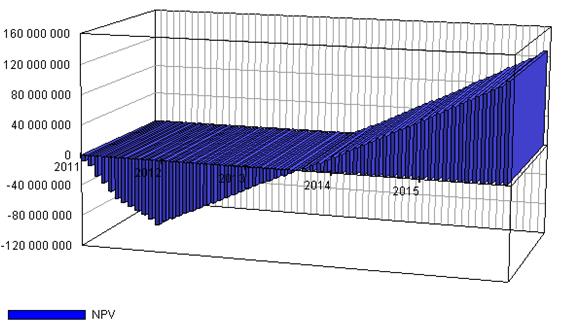
Рис. 4. Графическое представление чистого приведенного дохода в формате 3D-модели.
Оказывается возможным произвести визуальный анализ анализ чувствительности интегрального показателя эффективности в зависимости от неопределенных факторов, таких как объем сбыта, цена сбыта, ставки налогов, первоначальные затраты. Стоит отметить, что зависимости данного вида применяются для количественного и качественного анализа рисков результатов проекта, связанных с отклонениями случайных факторов в установленных диапазонах.
По осям абсцисс графиков анализа чувствительности откладываются диапазоны вариации неопределенных параметров, а по осям ординат диапазон изменения NPV или другого выбранного интегрального показателя в абсолютных единицах или относительных единицах.
Кроме того, часто используется трехмерная модель чистого приведенного дохода или выбранного показателя эффективности для визуального отображения рисков путем визуализации разброса значений. Как правило, анализ рисков эффекта от реализации проекта осущетсвляется при помощи метода Монте-Карло, который легко может быть представлен в форме 3D-модели.
Трехмерная диаграмма позволяет проводить наглядную визуальную интерпретацию бизнес-ситуации, связанной с рисками, поскольку унимодальность кривой позволяет судить о невысоком уровне риска.
Проекты с неопределенной структурой сети типа GERT
В том случае, когда структура сетевой модели проекта до конца не определена и события носят вероятностный характер, используется технология визуального анализа, основанная на стохастической структуре сети, называемая GERT (Graphical Evaluation and Review Technique) [18]. При реализации проектов возникают разнообразные отклонения в ходе реализации, вследствие которых характеристики конкретных работ принимают новые, отличные от планируемых, параметры.
Стохастическая сеть – сеть, которая может быть выполнена только при выполнении некоторого подмножества дуг [2]. Узлы сети можно интерпретировать как состояния системы, дуги переходы из одного состояния в другое [11; 13]. Каждый внутренний узел стохастической сети выполняет две функции. Одна из них касается входа в узел, а другая – выхода.
Входная функция – определяет условие, при котором узел может быть выполнен.
Выходная функция – определяет совокупность условий, связанных с результатом выполнения узла. Т.е. выходная функция определяет должны ли выполняться все операции, которым данным узел предшествует, или только одна из них [18].
Типы входных функций:
- «И». Узел выполняется, если выполнены все дуги, входящие в него.
- «ИЛИ». Узел выполняется, если выполнена любая дуга, входящая в него.
- «Исключающее ИЛИ». Узел выполняется, если выполнена ровно одна из входящих в него дуг.
Типы выходных функций:
- «И». Все дуги, выходящие из данного события, выполняются. Это детерминированный выход.
- «ИЛИ». Как минимум одна дуга, выходящая из вершины, выполняется.
- «Исключающее ИЛИ». Если узел выполняется, то будет выполнена ровно одна выходящая дуга.
На рис. 5 представлен пример визуального представление GERT-network, в вершинах которой расположены события с функцией «XOR» (событие 2 - на входе и выходе, событие 3 - на входе), с функцией «OR» (событие 1 - на входе и выходе, событие 0 и 3 - на выходе), причем входная функция 0 события сетевой модели имеет вид «AND». Проекты, содержащие вершины типа GERT, представляют собой широкий класс сетевых моделей, имеющих прикладное значение.
Рассмотрим пример, представленный на рис. 5, над дугами надписаны вероятности выполнения соответствующих операций проекта, представленного сетевой моделью типа GERT.
Количество возможных комбинаций реализации проекта оценивается как 25=32, однако не все из них логически реализуемы.
Графический анализ проекта, представленного сетевой моделью типа GERT, можно выполнять при помощи специального дерева вариантов, позволяющего выделить успешные и неуспешные варианты исходов, существенно сократив тем самым перебор. В вершинах дерева отображаются работы: в случае успешного выполнения без подчеркивания, в противном случае с подчеркиванием. Листья дерева помечаются буквами N - в случае негативного варианта, S - в случае положительного исхода.
При помощи дерева вариантов оказывается возможным построить функцию распределения вероятностей исходов проекта, вычислить математическое ожидание критического пути и критической стоимости.
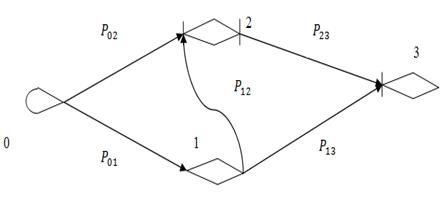
Рис. 5. Пример модели с недетерминированной структурой комплекса работ.
Ввод параметров сетевой модели, построение и визуальное отображение сетевых моделей типа GERT осуществляется при помощи пакета прикладных программ, разработанных автором [4; 5]. При помощи графического анализа проекта [4] удается выделить наиболее вероятные частичные варианты реализации [10].
Разработанные автором пакеты прикладных программ [4; 8] реализуют алгоритмы графического анализа вариантов, принимая во внимание вероятностные параметры комплекса работ, стоимостные и ресурсные характеристики операций. Следует отметить, что программные средства, направленные на визуальное решение задач подобного класса, позволяют оценить риски проектов, что особенно актуально для наукоемких проектов НИОКР (R&D - projects) с недетерминированными вариантами исходов.
Заключение
В статье рассмотрены вопросы визуального анализа задач управления проектами. Рассмотрены сетевые и линейные модели проекта, а также различные способы их визуального представления. Рассмотрена задача эквивалентного по времени и стоимости укрупнения комплекса работ, имеющая наглядную содержательную и визуальную интерпретацию, которая часто используется в решении задач управления и при принятии проектных решений менеджерами различных уровней.
Предложены подходы к решению задач, связанных с ресурсным планированием проектов и возникающими при этом графическими способами учета ресурсных ограничений, способствующими более эффективному и взвешенному принятию решений в сфере планирования и управления разработками с применением методов визуальной аналитики, разработанными автором.
Также были обсуждены задачи, касающиеся визуальных способов контроля и анализа оперативного управления ходом выполнения работ при помощи метода освоенного объема, позволяющего визуализировать прогресс или отставание в ходе реализации проекта.
Важным аспектом является также использование таких современных и актуальных методов визуализации бизнес-решений, как дорожные карты, преимущественно применяющиеся на стадии предпроектного исследования и анализа, планирования и прогнозирования результатов.
С целью решения задач, возникающих на стадиях инвестиционного и финансового планирования, при помощи визуальных методов анализа, используются диаграммы чистого приведенного дохода и качественного анализа рисков, в том числе и с применением метода Монте-Карло.
В статье рассмотрены методы визуального моделирования сетевых моделей проектов с недетерминированной структурой, опираясь на графическое представление исходов и методику GERT [2].
Наряду с аналитическим обзором существующих моделей и методов визуализации автор предлагает использование программных средств [1; 3-8], позволяющих решить поставленные задачи в сфере управления проектами.
Опираясь на собственный опыт, можно заметить, что далеко не все системы управления проектами, представленные в настоящее время на рынке, решают задачи визуализации проектной информации в том объеме, который был бы достаточен для раскрытия их потенциала в решении управленческих задач. Так, практически отсутствуют системы промышленного масштаба, занимающиеся методами исследования графических сетевых моделей GERT общего вида.
Подход, основанный на использовании дорожных карт с целью инновационного бизнес-планирования, также не поддерживается в настоящее время современными средствами автоматизации управления проектными разработками, тогда как интеграция данного метода планирования бизнеса с системами класса PMS является, по мнению авторов, весьма актуальной и своевременной. Спрос на подобные системы превышает в настоящее время предложение со стороны разработчиков как систем компьютерной визуализации, так и крупных бизнес-систем класса ERP, MRP.
Автор считает использование методов визуальной аналитики в управлении проектами современным и перспективным подходом к решению крупномасштабных задач в сфере промышленности, менеджмента, образования.
Рецензенты:
Карабасов Ю.С., д.т.н., профессор, президент НИТУ «МИСиС», г. Москва.
Зайцев И.В., д.т.н., профессор, зам. начальника отдела ГУМиБ ДПП ОАО «Нижегородская инжиниринговая компания «Атомэнергопроект», г. Нижний Новгород.
Библиографическая ссылка
Колычев В.Д. ПРОГРАММНАЯ РЕАЛИЗАЦИЯ ВИЗУАЛЬНЫХ МОДЕЛЕЙ УПРАВЛЕНИЯ ПРОЕКТАМИ // Современные проблемы науки и образования. 2014. № 3. ;URL: https://science-education.ru/ru/article/view?id=13219 (дата обращения: 11.02.2026).



