Сила сопротивления качению колеса складывается из Ffш - сопротивления качению колеса, обусловленного гистерезисными потерями в шине; силы сопротивления Ffс, обусловленной деформацией снежного полотна пути колесом машины; Ffэб - силы сопротивления от экскавационно-бульдозерных эффектов [4]; Ffфг - силы сопротивления движению от фрезерования настовой корки и внутримассивных ледяных прослоек [1-3, 8]:
![]()
Центральное место в теории взаимодействия движителя с деформируемой опорной поверхностью занимает вопрос о распределении напряжений в зоне контакта.
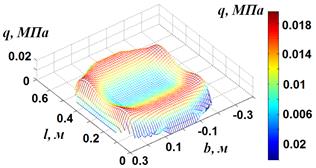
В результате проведенных экспериментальных исследований получены трехмерные эпюры распределений нормальных давлений в зоне контакта колес транспортных средств с опорной поверхностью при различных внутренних давлениях воздуха в шинах (рис. 1). Значения коэффициентов неравномерности распределения давлений для исследованных шин приведены в табл. 1.
 а
а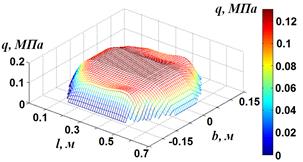 б
б
Рис. 2. Эпюра нормальных давлений в контакте шины с опорной поверхностью: а - для шины 1300х600-533 модели «ТРЭКОЛ» (pв = 0,01 МПа), б – для шины КИ-115АМ 12.00 R18 (pв = 0,09 МПа)
Необходимо стремиться к наиболее высокой точности определения силы сопротивления, обусловленного деформацией снежного полотна пути, так как она является причиной наибольших энергозатрат на передвижение машины [5]. На рис. 2 представлена блок-схема алгоритма расчета сопротивления от смятия снега с учетом данных о неравномерности распределения давлений в зоне контакта шины с опорной поверхностью. Следует особо подчеркнуть, что данная методика предусматривает возможность использования любой математической модели взаимодействия пневмоколесного движителя с деформируемой опорной поверхностью. Данные о распределении давлений могут быть получены как экспериментальным, так и расчетным путем с использованием вычислительных систем, основанных на методе конечных элементов [10]. Однако в рамках данной работы расчетный метод не рассматривается.
Сила сопротивления, обусловленная деформацией снежного полотна пути колесом машины, вычисляется по [9]:
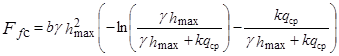
где k – коэффициент, характеризующий неравномерность распределения давлений в зоне контакта шин с опорной поверхностью, b – ширина колеса; γ – коэффициент начальной жесткости снега; hmax – коэффициент, характеризующий величину деформации снега при давлениях, соответствующих максимальному уплотнению, qср – среднее давление колес на опорную поверхность.
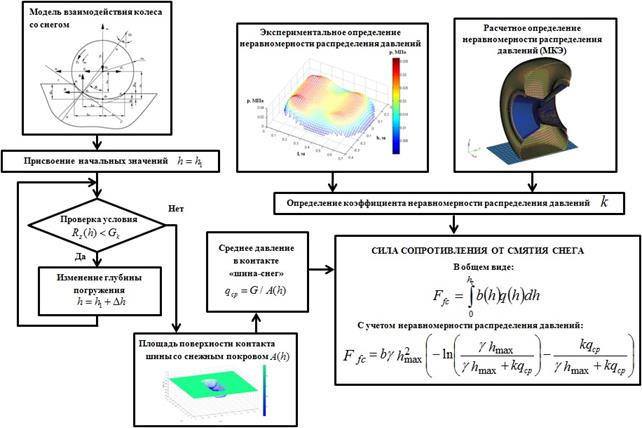
Рис. 2. Методика учета неравномерности распределения давлений в контакте шины с опорной поверхностью при расчете силы сопротивления от смятия снега
Коэффициент k рассчитан путем анализа полученных в результате экспериментальных исследований эпюр (при различных внутренних давлениях воздуха в шинах). Коэффициент k неравномерности распределения давлений – оценочный параметр, характеризующий отношение максимального (пикового) значения давления в зоне контакта шины с опорным основанием к среднему.
Значения коэффициента неравномерности распределения давлений для исследованных шин сведены в табл. 1 [6, 7].
Среднее давление на твердую опорную поверхность равно отношению нагрузки на колесо к площади контакта. В случае отсутствия точных данных о нагрузке на колесо следует определить объем эпюры либо получить сумму значений массива данных о распределении и разделить на число элементов массива. Пиковое давление определяется как максимальный элемент массива данных о распределении давлений по площади контакта колеса с опорной поверхностью.
Для нахождения объема, ограниченного поверхностью распределения нормальных давлений в пятне контакта и плоскостью ХоY, необходимо воспользоваться интегрированием.
В современных системах компьютерной математики, например, MATLAB, реализовано множество современных методов численного интегрирования. Численное интегрирование заключается в приближенном вычислении определенного интеграла одним из численных методов. В основе методов численного интегрирования лежит суммирование с (некоторыми весами) значений подынтегральной функции. При наличии экспериментальных данных подынтегральные функции, характеризующие распределения давлений, задаются таблицами (массивами данных). Прямоугольная область, пределам которой соответствуют пределы интегрирования, разбивается на меньшие прямоугольники. Для каждого прямоугольника рассматривается параллелепипед, построенный на этом прямоугольнике как на основании, и с высотой равной значению подынтегральной функции в центре прямоугольника. Интеграл заменяется на сумму объемов этих параллелепипедов.
Для определения среднего давления в контакте взаимодействия колеса со снежным полотном пути по одной из существующих математических моделей необходимо проделать последовательность следующих действий. Необходимо задаваться значениями погружения колеса в снег (произвести перебор возможных погружений) и рассчитывать величины реакции снега на колесо. Если реакция снега на колесо равна нагрузке на колесо, то колесо дальше в снег погружаться не будет и выбранные значения погружения являются истинными (итерации прекращаются), в противном случае следует увеличивать значение погружения до тех пор, пока условие равенства нагрузки и реакции снега на колесо не выполнится.
В результате будет получена глубина погружения пневмоколесного движителя в снег и, соответственно, возможная поверхность контакта, площадь которой необходима для расчета величины среднего давления в контакте пары «шина-снег». В итоге будут получены все составляющие формулы расчета сопротивления от смятия снега колесом машины.
Рассмотрим, как учет реального характера распределения давления в зоне контакта колеса с опорной поверхностью влияет на точность расчета силы сопротивления от смятия снега.
На рис. 3 представлены гистограммы, позволяющие оценить, как влияет учет полученных коэффициентов на расхождения (ошибку) при расчете величины сопротивления при разной глубине снега.
Таблица 1
Обобщающие параметры колесных движителей
|
Тип шин Параметры |
Шины с регулируемым давлением |
Шины сверхнизкого давления |
Сельскохозяйственные шины |
Грузовые шины |
|
Диапазон нагрузок, кН |
15-45 |
4-17 |
10-50 |
9 – 50 |
|
Диапазон внутренних давлений, МПа |
0,1-0,75 |
0,01-0,1 |
0,045-0,24 |
0,2 –0,75 |
|
Наружный диаметр, м |
0,9 – 1,4 |
0,9 – 1,7 |
0,9 – 1,7 |
0,9 – 1,4 |
|
Коэффициент ширины шины B/D |
0,25-0,36 |
0,32-0,54 |
0,25 – 0,62 |
0,25 – 0,35 |
|
Коэффициент неравномерности распределения давлений, k |
1,1-1,35 |
1,13 – 1,61 |
1,42 – 1,91 |
1,34 – 1,42 |
Необходимо отметить, что данные диаграммы построены при разном внутреннем давлении воздуха в шинах, поэтому также можно оценить расхождения между расчетными величинами сопротивлений при подстановке среднего давления колеса в контакте в формулу расчета и результатами расчета сопротивлений с учетом коэффициентов неравномерности распределения давлений в контакте.
Из рис. 3 отчетливо видно, что для шин с регулируемым давлением с увеличением глубины снега расхождения в расчетных данных растут. Причем, чем больше величина внутришинного давления воздуха, тем значительнее рост расхождения между расчетными данными о сопротивлениях. Что объясняется увеличением неравномерности контактных напряжений при увеличении давления воздуха в шинах.
Для шин сверхнизкого давления наблюдается противоположная картина. При снижении величины внутреннего давления воздуха в шинах наблюдается увеличение расхождения между расчетными данными о сопротивлениях. Что объясняется увеличением неравномерности контактных напряжений при снижении давления воздуха в шинах.
Общую картину влияния учета полученных коэффициентов на расчетную величину сопротивления от смятия снега в зависимости от задаваемой глубины снежного покрова, а также внутреннего давления воздуха в шинах отражают представленные на рис. 5 поверхности. Поверхности построены для двух типов снега, поэтому можно сделать и некоторые выводы о влиянии учета коэффициентов неравномерности на величину сопротивления при разной плотности снега.
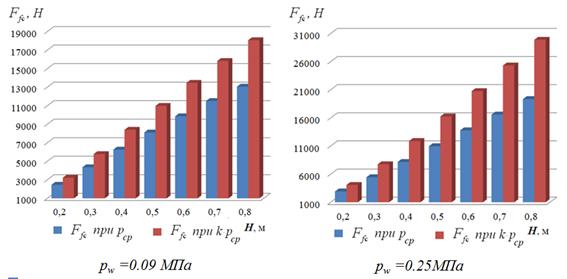
![]() Подстановка среднего давления колеса в контакте в формулу расчета
Подстановка среднего давления колеса в контакте в формулу расчета
![]() Расчет сопротивления с учетом коэффициентов неравномерности распределения давлений
Расчет сопротивления с учетом коэффициентов неравномерности распределения давлений
Рис. 3. Влияние учета полученных коэффициентов на расчетную величину сопротивления от смятия «снега-2» шинами КИ-115АМ 12.00 R18
Из графиков видно, что с увеличением плотности снега расхождения в расчетных данных уменьшаются, что особенно проявляется при низких давлениях воздуха в шинах.
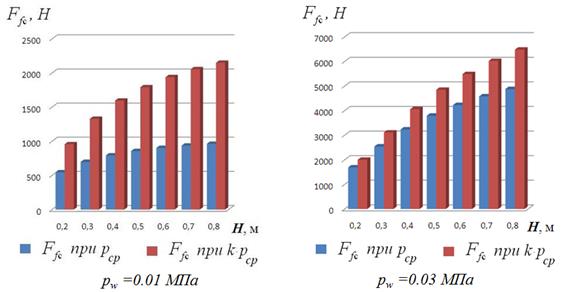
![]() Подстановка среднего давления колеса в контакте в формулу расчета
Подстановка среднего давления колеса в контакте в формулу расчета
![]() Расчет сопротивления с учетом коэффициентов неравномерности распределения давлений
Расчет сопротивления с учетом коэффициентов неравномерности распределения давлений
Рис. 4. Влияние учета полученных коэффициентов на расчетную величину сопротивления от смятия «снега-2» шинами ТРЭКОЛ 1300х600-533
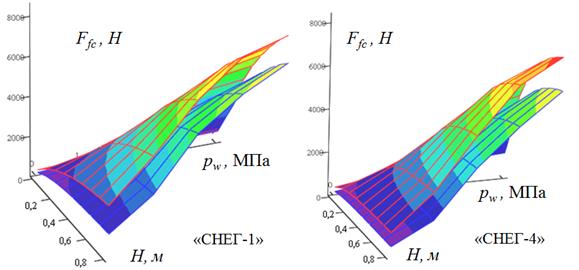
Рис. 5. Характер изменения сопротивления от смятия Ffc в зависимости от глубины снега H и давления воздуха в шинах pw
В результате проведенных исследований установлено, что расхождения между расчетной величиной сопротивления от смятия снега без учета неравномерности распределения давлений в контакте шины с опорной поверхностью и результатом расчета сопротивления с учетом полученных коэффициентов неравномерности для различной глубины и плотности снежного покрова могут составлять от 25 до 70%.
Исследования проведены при поддержке «грантов Президента РФ» № 14.124.13.1869-МК «Разработка метода повышения эффективности использования транспортно-технологических машин в зимний период на основании экспериментально-теоретических исследований».
Рецензенты:
Молев Ю.И., д.т.н., профессор кафедры «Строительные и дорожные машины» «Нижегородский государственный технический университет им. Р.Е.Алексеева», г. Нижний Новгород.
Кравец В.Н. д.т.н., профессор кафедры «Автомобили и тракторы» «Нижегородский государственный технический университет им. Р.Е.Алексеева», г. Нижний Новгород.
Библиографическая ссылка
Зезюлин Д.В., Макаров В.С., Беляков В.В. МЕТОДИКА РАСЧЕТА СОПРОТИВЛЕНИЯ КАЧЕНИЮ КОЛЕСА ПО СНЕЖНОМУ ПОЛОТНУ ПУТИ С УЧЕТОМ НЕРАВНОМЕРНОСТИ РАСПРЕДЕЛЕНИЯ ДАВЛЕНИЙ В ЗОНЕ КОНТАКТА // Современные проблемы науки и образования. 2014. № 3. ;URL: https://science-education.ru/ru/article/view?id=13210 (дата обращения: 30.01.2026).



