Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Ануфриев И.С. 1, 2 Шадрин Е.Ю. 1, 2

---

1 ФГБУН Институт теплофизики им. С.С. Кутателадзе СО РАН

2 ФГБОУ ВПО "Новосибирский национальный исследовательский государственный университет" (НГУ)

Теоретически рассматривается динамика акустических возмущений в однородной двухфазной среде (газ с твердыми частицами) с неравновесной химической реакцией в газовой фазе. Газовзвесь считается квазиравновесной по скоростям и температурам фаз, что характерно в случае достаточно малого размера частиц. Проанализирована линейная задача об устойчивости с учетом кинетико-волнового взаимодействия и диссипативных эффектов. Обоснованы оценки диссипативных эффектов и масштабов неустойчивости для условий, характерных для зоны реакции в детонационной волне. Значительное повышение диссипации за счет межфазного обмена импульсом и теплом приводит к ослаблению (устойчивости) возмущений с длиной волны, сопоставимой с размером детонационной ячейки. Как следствие, диссипация может существенно влиять на пространственную структуру детонации в запыленных средах, ослабляя неоднородность волны и способствуя срыву детонационного режима.

Статья в формате PDF

152 KB

газовзвесь

детонация в запыленных средах

кинетико-волновое взаимодействие

межфазный обмен

устойчивость

1. Борисов А.А., Шарыпов О.В. Моделирование структуры неустойчивого фронта газовой детонации // Известия СО АН СССР. Серия технические науки. – 1989. – Вып. 2. – С. 50-55.

2. Борисов А.А., Шарыпов О.В. О формировании волны пузырьковой детонации // Известия СО АН СССР. Серия технические науки. – 1990. – Вып. 2. – С. 50-59.

3. Борисов А.А., Шарыпов О.В. Самоподдерживающиеся уединенные волны в неравновесных средах // Физика горения и взрыва. – 1993. – Т. 29, № 4. – С. 80-87.

4. Шарыпов О.В. Диссипативные эффекты и детонация в запыленных средах // Физика горения и взрыва. – 2014. – Т. 50, № 4.

5. Шарыпов О.В. Квазилинейные модели автоволн в многофазных средах с горением.. – LAP LAMBERT Academic Publishing GmbH & Co. KG, Saarbrücken, 2011. ISBN 978-3-8443-5423-2.

6. Borissov A.A., Sharypov O.V. Physical Model of Dynamic Structure of the Surface of Detonation Wave / In: Dynamic Structure of Detonation in Gaseous and Dispersed Media. – Ed. by A.A. Borissov, Kluwer Academic Publishers, Netherlands, 1991. – P. 77-108.

7. Borissov A.A., Sharypov O.V. Self-sustained solitary waves in non-equilibrium media // J. Fluid Mech. – 1993. – Vol. 257. – P. 451-461.

8. Papalexandris M.V. Numerical simulation of detonations in mixtures of gases and solid particles // J. Fluid Mech. – 2004. – Vol. 507. – P. 95-142.

9. Sharypov O.V., Anufriev I.S. Model of evolution of finite-amplitude perturbations in a two-phase reactive system // Heat Transfer Research. – 2012. – Vol. 43, No. 2. – P. 109-122. DOI: 10.1615/HeatTransRes.v43.i2.20

10. Wolanski P., Liu J.C., Kauffman C.W., Nicholls J.A., Sichel M. The effect of inert particles on methan-air detonations // Archivum Combust. – 1988. – Vol. 8, No. 1. – P. 15-32.

Введение

Известный эффект усиления акустических возмущений в зоне горения вызывает формирование характерной ячеистой структуры газовой детонации. Данная неустойчивость необходима для детонационного режима, поскольку самоподдерживающиеся одномерные детонационные волны не наблюдаются. Для газовой детонации диссипация, связанная с вязкостью и теплопроводностью среды, слаба и не оказывает влияния на ячеистую структуру волны. Мелкие химически инертные твердые частицы, добавляемые в реакционно способную газовую смесь, могут заметно снижать скорость детонационной волны [10]. Это объясняется потерями энергии на ускорение и нагрев частиц. При достаточно высокой концентрации дисперсной фазы детонационный режим невозможен [8, 10]. Критическое значение массовой концентрации твердой фазы зависит от размера частиц. С уменьшением размера эффект ослабления детонации возрастает. Увеличение удельной межфазной поверхности означает интенсификацию обмена импульсом и теплом, т.е. повышение потерь энергии волны. Этот механизм может быть описан в рамках одномерной модели без учета неустойчивости пространственной структуры волны. Если частицы очень малы (характерное время установления равновесия по скоростям и температурам фаз намного меньше времени реакции), то потери энергии приближаются к максимальному уровню и не должны зависеть от размера частиц: суспензия квазиравновесна (температуры и скорости фаз одинаковы почти во всей зоне реакции). В то же время расчеты демонстрируют существенное влияние диаметра частиц на двумерный детонационный режим даже для очень мелких частиц [8]: детонационный фронт становится гладким, поперечные волны ослабляются, и размер ячейки увеличивается. Предложенное объяснение [9] основано на факте сильного увеличения диссипативных эффектов в квазиравновесной суспензии. Диссипация энергии акустических возмущений за счет межфазного обмена импульсом может в 100–1000 раз превышать диссипацию в чистом газе. Это может обеспечивать устойчивость возмущений с длиной волны порядка характерного масштаба детонационной ячейки [4]. Как следствие, детонационный режим может быть подавлен (будет наблюдаться срыв детонации).

В работе [7] выведено нелинейное эволюционное уравнение, описывающее распространение волн малой, но конечной амплитуды в однофазной газовой среде с неравновесным экзотермическим процессом; получено решение в виде одномерной самоподдерживающейся уединенной автоволны. Согласно [2,3,5,7], для длинных волн модель может быть сведена к эволюционному уравнению типа уравнения Бюргерса с «отрицательной вязкостью». Это означает неустойчивость и усиление возмущений, длина волны которых определяется отношением между тепловыделением и диссипацией энергии. Слабая диссипация в газовой среде оказывает влияние на возмущения с длиной волны, намного меньшей масштаба реакции.

Аналогичная задача для газовзвеси рассмотрена в работе [9]. Получены аналитические результаты для двух предельных случаев: а) мелкие частицы (квазиравновесие фаз); б) крупные частицы. Было показано, что зависимости диссипации от размера частиц в этих случаях существенно различаются. В первом случае характерные времена установления равновесия скоростей и температур фаз намного меньше, чем период возмущений (и время реакции). Масштаб доминирующего неустойчивого возмущения при этом может значительно измениться по сравнению с чисто газовой средой. Для крупных частиц (т.е. для высокочастотных возмущений) период доминирующей неустойчивости приблизительно тот же, что и в чистом газе. Это обусловливает различие влияния мелких и крупных частиц на пространственную структуру зоны реакции.

Основываясь на подходах, указанных выше, в настоящей работе представлен анализ возможности подавления акустических возмущений, масштаб которых сравним с длиной зоны реакции, за счет высокой диссипации энергии в квазиравновесной взвеси инертных твердых частиц в реагирующей газовой смеси.

Постановка задачи

Проанализируем распространение плоских возмущений в неограниченной газовзвеси, содержащей в единице объема m химически инертных твердых частиц с радиусом r1 = const и плотностью ρ1 = const. В отсутствие возмущений скорость каждой из фаз равна нулю. Твердая фаза занимает малую долю объема среды . Это позволяет пренебречь взаимодействием частиц, а также парциальным давлением и вязкостью облака частиц. Будем предполагать, что длина волны возмущения намного превосходит среднее расстояние между частицами. Соответственно, будем использовать модель однородной двухкомпонентной неравновесной смеси (учитывая различие скоростей и температур фаз). Массовая скорость u, плотность ρ, давление p, температура T и удельная энтропия S газа являются величинами, осредненными по объему, содержащему большое количество частиц. Возмущения имеют малую амплитуду: , где , , , , ε – малый параметр. Индекс 0 обозначает невозмущенное состояние среды, Cf – адиабатическая скорость звука в газе, индекс f означает условие Y = const (т.е. высокочастотные возмущения, относительно которых реакция «заморожена»), Y – массовая доля продуктов реакции. Уравнения неразрывности и сохранения импульса (без учета гравитации) для каждой из фаз имеют вид:

(1)

(2)

(3)

(4)

где u1 – возмущение скорости облака частиц, ν – кинематическая вязкость газа, 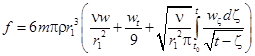– сила сопротивления облака частиц в единице объема. Если радиус r1 достаточно мал, то характерное время изменения относительной скорости фаз намного меньше, чем величина . Следовательно, первое слагаемое (сила Стокса) является определяющим в выражении для f, и можно пренебречь вторым и третьим слагаемыми. Сила сопротивления Стокса вызывает изменение скорости частиц с характерным временем . Ограничивая анализ случаем низкочастотных возмущений, подставим в уравнения (3) и (4). Тогда из (4) получим:

(5)

Неравновесная химическая реакция в газовой фазе (предварительно перемешанные реагенты) характеризуется объемной скоростью производства продуктов реакции ω и удельным тепловыделением Q. Представим реакцию в форме одноступенчатого превращения «реагенты → продукты реакции» с кинетическим уравнением общего вида:

(6)

Закон сохранения энергии с учетом термодинамических соотношений может быть представлен в форме уравнения для производства энтропии газа:

, (7)

где s – производство энтропии за счет внутреннего трения в газовой фазе, оно пропорционально , – удельная теплоемкость газа при постоянном давлении, c – температуропроводность газа, – удельное количество тепла, передаваемое частицам в единицу времени, тепловой поток на поверхности отдельной частицы определяется из решения задачи о центрально-симметричном распределении температуры в твердом шаре с радиусом r1, плотностью r1, температуропроводностью c1 и удельной теплоемкостью c1 с граничным условием и начальным условием [9]. Для длинноволновых возмущений характерное время тепловой релаксации частицы гораздо меньше, чем характерное время изменения температуры (периода возмущения). В этом случае , где .

Уравнение состояния газа с химической реакцией запишем в общем виде:, или: Используя уравнения (6) и (7), уравнение состояния можно преобразовать, пренебрегая членами , к следующему [7]:

(8)

где , , , . С помощью уравнений (6)-(8) тождество может быть представлено в форме:

(9)

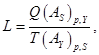
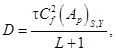
где – характерное время реакции, – скорость распространения низкочастотных возмущений в реагирующем газе.

Результаты исследования устойчивости

Все величины в уравнениях (1), (3), (5) и (9) приведем к безразмерной форме с помощью параметров . Рассмотрим распространение возмущений в одном направлении, введя сопровождающую систему координат , движущуюся со скоростью . Профиль возмущения медленно изменяется в этой системе отсчета: . При из уравнения (5) получим: [9]. После исключения переменных можно записать линейное уравнение для одной переменной :

(10)

где , , γ – показатель адиабаты газовой смеси.

Решение уравнения (10) можно представить в форме суперпозиции гармоник и получить дисперсионное соотношение:

(11)

Для высокочастотных (относительно ) возмущений: . В данном предельном случае дисперсионное соотношение описывает затухание возмущений за счет диссипации в двухфазной среде, тепловыделение не влияет на динамику возмущений. Скорость распространения возмущений в двухфазной среде отличается от адиабатической скорости звука в газе: .

В случае низкочастотных возмущений дисперсионное соотношение учитывает влияние химической реакции:

(12)

Коэффициенты в уравнении (12) могут изменять знаки. Если выполнен критерий , то бесконечно малые возмущения нарастают за счет преобладания тепловыделения над диссипацией (см. рис. 1). Скорость распространения низкочастотных возмущений отличается от на величину, которая определяется кинетикой реакции.

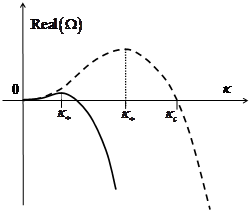
Рис. 1. Инкремент возмущений при условии : чистый газ, (пунктирная линия) и газовзвесь с мелкими частицами, (сплошная линия)

Из соотношения (11) можно найти значение волнового числа наиболее неустойчивого возмущения, а также критическое волновое число , разделяющее устойчивые и неустойчивые гармоники:

Обсуждение и выводы

Для чистого газа характерна слабая диссипация энергии возмущений: . Здесь для оценки приняты значения: с, м/с, вязкость и температуропроводность м2/c. Для детонации характерное значение тепловыделения: . Тем самым, в газовой среде и м. Такое значение намного меньше характерного масштаба зоны реакции и размера ячейки м, и соответственно, диссипация не влияет на пространственную структуру детонационной волны [1, 6].

В квазиравновесной газовзвеси , если м, , . Следовательно, и . Это означает, что диссипация в газовзвеси с мелкими инертными твердыми частицами может оказывать существенное влияние на пространственную структуру детонации. Подавляя неустойчивость, высокая диссипация приводит к ослаблению поперечных волн и способствует срыву детонационного режима.

Наряду с эффективным подавлением акустических возмущений, мелкие частицы в меньшей степени возмущают поток газа (по сравнению с крупными частицами), поскольку возмущения с масштабом м быстро затухают даже в чистом газе.

При распространении детонации в покоящейся среде на некотором расстоянии за ударным фронтом волны (при достаточно высоком значении соответствующего числа Рейнольдса) происходит переход от ламинарного к турбулентному пограничному слою. В ядре потока в зоне реакции тоже возникают турбулентные пульсации, если число Рейнольдса превышает критическое значение. Можно предположить, что повышение диссипативных свойств среды за счет межфазного обмена импульсом должно задерживать ламинарно-турбулентный переход как в ядре потока, так и в погранслое. Данный механизм тоже способствовал бы ослаблению пространственной неоднородности волны и срыву детонации.

Куйбин П.А., д.ф.-м.н., ученый секретарь, ФГБУН Институт теплофизики им. С.С. Кутателадзе Сибирского отделения Российской академии наук (ИТ СО РАН), г. Новосибирск;

Шарыпов О.В., д.ф.-м.н., профессор, ФГБОУ ВПО «Новосибирский национальный исследовательский государственный университет» (НГУ), г. Новосибирск.

Библиографическая ссылка