Впервые физико-математическая модель лесного пожара была предложена А.М. Гришиным [1; 8] и усовершенствована его учениками [2; 3; 6]. В более поздних работах постановка была дополнена фазой, соответствующей свободной воде [5; 7]. В работе [5] свободная вода представляла собой барьер, который переходил вазообразное состояние под действием энергии пожара. В работе [7] поток воды задавался равномерным, постоянным и не зависящим от динамики пожара. Для численного моделирования использовался метод крупных частиц, адаптированный для моделирования лесных пожаров [4]. В отличие от данных работ, в настоящей статье рассматривается тушение пожара с помощью водяной пушки с заданным расходом воды и её разбросом, осуществляющей подачу воды с учётом динамики пожара.
Водная пушка производит обстрел по выбранной точке с разбросом по нормальному закону.
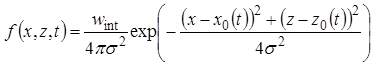, (1)
где 
, 
– координаты точки прицела водяной пушки; 
– массовый расход воды на метр фронта, кг/(м·с); 
- интенсивность подачи воды, отнесённая к объёму, кг/(м3·с); 
, м – среднеквадратическое отклонение, обуславливающее дальность разлёта частиц воды от точки прицела. Общая физическая постановка задачи показана на рис. 1.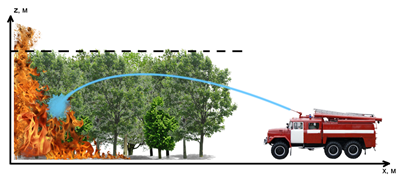 
Рис. 1. Физическая модель подачи воды в зону горения
Высота леса постоянна. Капли воды считаются такими, что, долетая до цели, испаряются полностью. Точка обстрела принадлежит слою леса и имеет температуру выше Tcr = 800 K, расстояние точки до источника подачи воды не превышает радиуса его действия. Данные условия являются необходимыми для выбираемой точки во всех рассмотренных случаях. Необходимо определить, при какой минимальной интенсивности воды wint пожар будет потушен.
1 сценарий. Для обстрела выбирается точка с максимальной температурой.
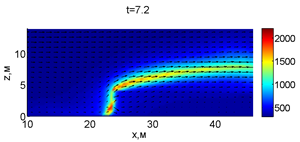
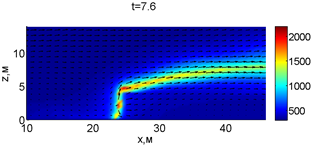
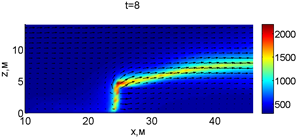
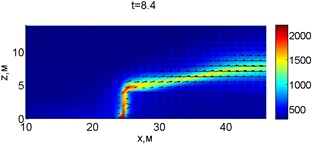
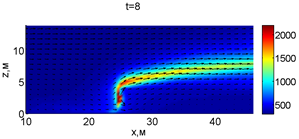
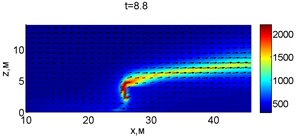
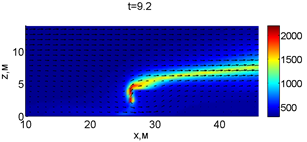
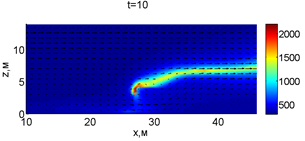
Для успешного тушения пожара при выборе точки с максимальной температурой необходимое минимальное значение интенсивности воды wint = 2,937 кг/(м·с). Поля скоростей и температур для этого случая показаны на рис. 2.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
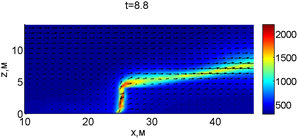
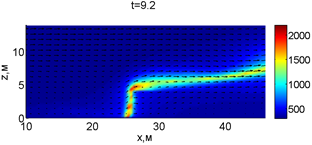
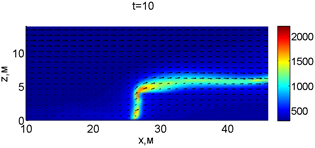
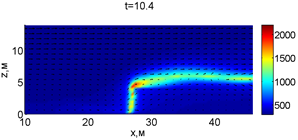
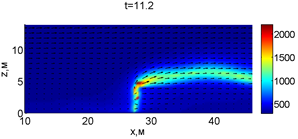
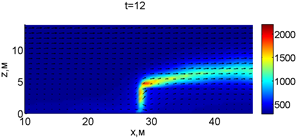
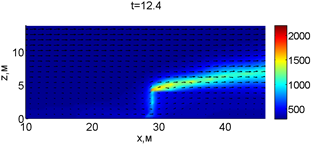
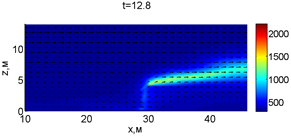
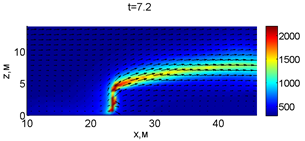
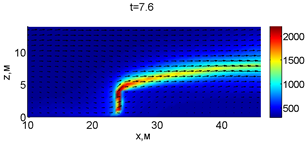
Рис. 2. Динамика распространения пожара при обстреле точки с максимальной температурой
В момент времени 7,2 с происходит разрыв фронта пожара. Затем на 7,6-8 с область высоких температур переходит от нижней части слоя к верхнему. В момент времени 8,4 с можно наблюдать восстановление фронта пожара, что, однако приводит к уменьшению его скорости распространения. В 8,8 с видно, что распространение газовой фазы направлено к верхней части леса, после чего пожар постепенно затухает. В 11,2 с возникает вспышка в верхних слоях лесополосы, которая тушится к 12,8 с.
2 сценарий. Выбор дальней точки. Выбирается точка с минимальной высотой, если несколько точек имеют одинаковую высоту, то предпочтение отдаётся точке, находящейся на максимальном расстоянии от источника воды.
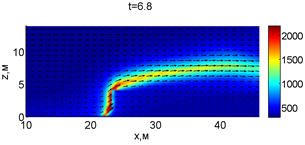
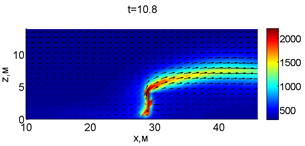
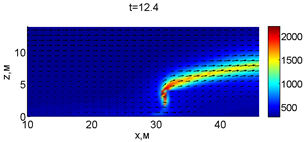
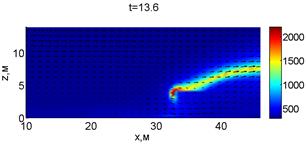
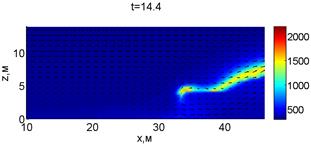
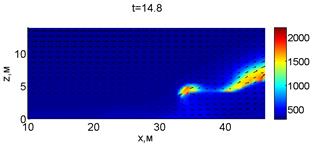
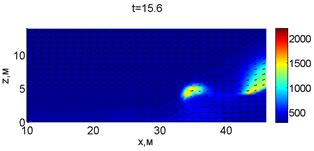
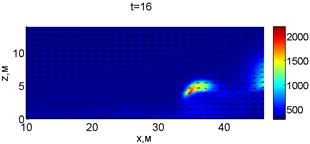
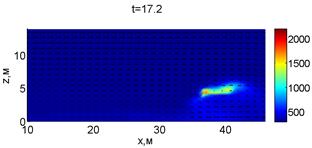
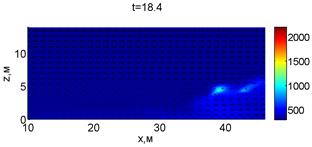
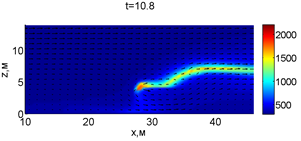
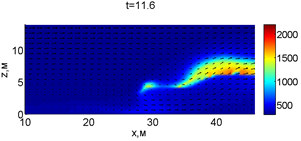
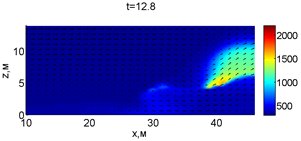
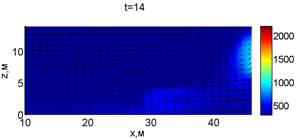
Для успешного тушения пожара при выборе самой дальней точки необходимое минимальное значение интенсивности воды wint = 0,577 кг/(м·с). Динамика для этого случая показана на рис. 3. Отличительным характером данного случая от первой ситуации является отсутствие разрыва фронта пожара. В момент времени 10,8 с наблюдается снижение температуры в нижней части леса. В течение всего следующего развития пожара можно наблюдать его плавный переход в верхние слои леса. В моменты времени 14.8 и 16 с наблюдаются вспышки в верхней части лесополосы. К моменту 18,4 с пожар полностью потушен.
3 сценарий. Выбор ближней точки. Выбирается точка на минимальной высоте, если несколько точек имеют одинаковую высоту, то предпочтение отдаётся точке, находящейся на минимальном расстоянии от источника воды.
Для успешного тушения пожара при выборе самой ближней точки необходимое минимальное значение интенсивности воды wint = 0,712 кг/(м·с). Динамика для этого случая показана на рис. 4. Динамика пожара сходна с предыдущим случаем, но не наблюдаются вспышки в верхней части леса. Уже в момент времени 7,6 с можно наблюдать отсутствие высоких температур в нижней части леса. Со временем пожар вытесняется из нижней части слоя. К 14 с происходит полное затухание пожара.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3. Динамика распространения пожара при обстреле дальней точки
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4. Динамика распространения пожара при обстреле ближней точки
В таблице 1 приведены результаты численных экспериментов по моделированию пожара при заданной критической температуре. Также были проведены серии моделирования с модификациями для всех трех случаев, описанных выше. Для 1-го сценария - увеличение дисперсии распределения разброса воды для выбранной точки (сценарий 7), обстрел точки с максимальной температурой при минимальной высоте (сценарий 4), увеличение дисперсии разброса воды для выбранной точки с максимальной температурой при минимальной высоте (сценарий 10). Для 2-го и 3-го сценариев - увеличение минимальной высоты обстрела hcr (сценарии 5 и 6 соответственно), увеличение дисперсии распределения разброса воды для выбранной точки (сценарии 8 и 9 соответственно), увеличение дисперсии распределения разброса воды и увеличение минимальной высоты обстрела hcr (сценарии 11 и 12 соответственно).
Таблица 1
Сравнение зависимости интенсивности подачи воды от выбора стратегии обстрела
|
Сценарий |
Дисперсия распределения Гаусса, м |
Минимальная высота hcr, м |
Критическая интенсивность подачи воды, кг/(м·с) |
|
1 |
0,5 |
0,2 |
2,937 |
|
2 |
0,5 |
0,2 |
0,577 |
|
3 |
0,5 |
0,2 |
0,712 |
|
4 |
0,5 |
0,6 |
1,023 |
|
5 |
0,5 |
0,6 |
0,718 |
|
6 |
0,5 |
0,6 |
0,982 |
|
7 |
1 |
0,2 |
2,832 |
|
8 |
1 |
0,2 |
0,771 |
|
9 |
1 |
0,2 |
0,978 |
|
10 |
1 |
0,6 |
1,245 |
|
11 |
1 |
0,6 |
1,091 |
|
12 |
1 |
0,6 |
1,287 |
Таким образом, в силу упрощенности модели, из результатов моделирования видно, что самым оптимальным выбором обстрела будет дальняя точка (сценарий 2), температура которой больше критической температуры Tcr = 800 K. Если минимизировать высоту обстрела, то можно в разы уменьшить расход воды при обстреле точки с максимальной температурой. Изменение дисперсии распределения Гаусса уменьшает интенсивность подачи воды только в случае обстрела точки с максимальной температурой, для всех остальных случаев – увеличивает. Изменение высоты во всех случаях увеличивает расход воды.
Следует отметить, что в используемой модели не учитываются потери воды на испарение при прохождении через слой нагретой газовой фазы при стрельбе в тыл пожара.
Рецензенты:
Петрухин Н.С., д.ф.-м.н., научный руководитель Нижегородского филиала Национального исследовательского университета «Высшая школа экономики», г. Нижний Новгород.
Юнаковский А.Д., д.ф.-м.н., профессор, ведущий научный сотрудник ФГБУН «Институт прикладной физики Российской академии наук», г. Нижний Новгород.
Библиографическая ссылка
Нищенков В.В., Романова Н.А., Катаева Л.Ю., Катаева Л.Ю., Масленников Д.А., Лощилов А.А. ОБ ОПТИМАЛЬНОЙ СТРАТЕГИИ ТУШЕНИЯ ЛЕСНОГО ПОЖАРА ВОДЯНОЙ ПУШКОЙ // Современные проблемы науки и образования. 2014. № 3. ;URL: https://science-education.ru/ru/article/view?id=13179 (дата обращения: 10.05.2025).