Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Бамадио Б... 1 Семенчин Е.А. 1

---

1 ФГБОУ ВПО «Кубанский государственный университет»

В работе описана методика построения количественной оценки принятия решения о выдаче кредитующей организацией (банком) кредита предприятию-заемщику в условиях многокритериальной оптимизации. Математическая модель принятия такого решения представляет собой двухкритериальную задачу: первый критерий, который необходимо максимизировать, описывает средний доход кредитующей организации, второй критерий, который необходимо минимизировать – величина риска не получить желаемый доход. Данная двухкритериальная задача решается методом линейной свертки, в которой коэффициенты выбираются не экспертами, а с помощью специально разработанного алгоритма. Использование указанной методики на практике позволяет экспертам кредитующей организации (банку) ускорить принятие решения о возможности выдачи предприятию требуемого кредита, принимать более обоснованные и взвешенные решения о его выдаче.

Статья в формате PDF

138 KB

свертка критериев

средний ожидаемый доход

матрица последствий

банкротство

финансовое состояние предприятия

Многокритериальная оптимизация

принятие решения

1. Астахов В. П. Анализ финансовой устойчивости фирмы и процедуры, связанные с банкротством. – М.: Ось–89, 1995. – 80 с.

2. Бамадио Б. Оценка кредитоспособности предприятий – заемщиков России и Мали // Известия кубанского государственного университета. Естественные науки. – Вып. № 1 (2). –2013. – С. 57–61.

3. Бамадио Б. Основные аспекты оценки кредитоспособности предприятий – заемщиков России и Мали // Международный журнал прикладных и фундаментальных исследований. –2013. – № 1. – С. 139–140.

4. Бамадио Б., Семенчин Е.А. Меры нечеткости множеств, порождаемых моделью Альтмана // Фундаментальные исследования. – 2013. – № 1. – С. 750–753.

5. Бамадио Б., Семенчин Е.А. Определение рисков в методике Бивера оценки финансового состояния предприятия / Б. Бамадио, Е.А. Семенчин // Тенденции и перспективы: Материалы международной научно-практической конференции. Сочи, 24/01 – 26/01. 2013 г. – С. 23–24.

6. Бамадио Б., Семенчин Е.А. Применение нейросетевых технологий для оценки кредитоспособности предприятий // Фундаментальные исследования. – 2013. – № 11 (часть 4). – С. 651–655.

7. Открытое Акционерное Общество «Ленмолоко»: [Электронный ресурс] // – Режим доступа: URL: http://www.len-moloko.spb.ru/documents/balance.html/. (Дата обращения: 01.10.2013).

8. Штойер Р. Многокритериальная оптимизация: теория, вычисления, приложения. – М.: Радио и связь, 1992. – 504 с.

9. Bamadio B., Semenchin E.A. Beaver’s technique of risk assessment in the estimation of the financial positions of companies // European journal of natural history. – 2013. – № 5. – P. 12–14.

Цель данной работы: разработать математическую модель принятия решения кредитором о выдаче кредита предприятию – заемщику, основанную на методике свертки критериев в многокритериальных задачах.

Пусть предприятие обращается к кредитору с просьбой предоставить ему кредит на срок от до лет, . На момент выдачи кредита оно может принадлежать одной из трех групп: группа I – благополучное финансовое состояние предприятия, группа II – финансовое состояние предприятия таково, что оно находится в состоянии «за 5 лет до банкротства», группа III – «за год до банкротства». Принадлежность кредитуемого предприятия к одной из трех групп I, II, III определяется с помощью показателей Бивера , [1]: к каждой из этих групп предприятие может принадлежать, если не менее трех показателей Бивера указывают на принадлежность к этой группе.

Предположим, что лицо, принимающее решения (ЛПР) со стороны кредитующей организации (банка), рассматривает возможных варианта принятия решения (стратегии): – выдавать, – выдавать, не более, чем на , , лет, – не выдавать кредит. Обозначим через – событие, означающее, что -й показатель (коэффициент Бивера) принадлежит -й группе, , .

Если известны статические (бухгалтерские) данные предприятия на протяжении лет, то на основе этих данных можно вычислить коэффициенты У. Бивера , и вероятности того, что коэффициент принадлежит -й группе, , [2 – 6,9].

В теории принятия решений предлагается, что ЛПР принимает решения, исходя из состояний некоторой среды, которая полностью определяется этими состояниями (состояния среды часто называют её стратегиями). В данном случае среда может находиться в одном из следующих состояний (иметь стратегии): всевозможные стратегии для первой группы –

,        ,       

 ,       ,        

 ,       ,         ,

,      ,       ,

,       ,        ,

;

всевозможные стратегии для второй группы –

,     ,      ,

,      ,       ,

,       ,     ,

,     ,    ,

,     ,      ,

;

всевозможные стратегии для третьей группы –

,      ,    ,

,      ,    ,

,       ,    ,

,      ,      ,

,        ,      ,

.

Таким образом, среда имеет , , стратегий: , , . Обозначим стратегии среды следующим образом: .

Учитывая независимость и вычисленные вероятности , легко вычислить вероятности , ; . По вероятностям можно определить вероятности , : ,,, ,,,,,. Обозначим через – ожидаемый доход в момент за предоставление кредита, если ЛПР выбрало – ю, , , а среда – свою – ю, , стратегию . Элементы можно упорядочить в виде матрицы последствий . Элементы , , , матрицы обычно задают (указывают) эксперты. Процедуру оценки элементов можно немного упростить, если использовать для этого следующие соображения. Обозначим через – доход, который кредитующая организация (банк) желает получить с кредитуемого предприятия за предоставление ему кредита, если ЛПР (выступающее со стороны кредитора) будет использовать стратегию , . В этом случае для оценки можно использовать очевидное соотношение: , , .

Пусть – средний доход, который получит кредитующая организация, если ЛПР (выступающее от имени этой организации) примет решение использовать стратегию , – величина риска не получить требуемый доход при использовании стратегии , , , где – символ дисперсии.

Тогда задача принятия решения о выдаче кредита предприятию-заемщику сводится к двухкритериальной задаче:

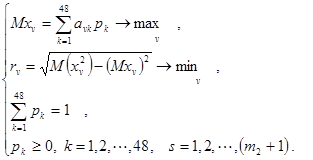(1)

Решать такие задачи можно методами свертки критериев, в частности, линейной свертки. Укажем один способ решения такого рода задачи.

Пусть рассматривается задача многокритериальной оптимизации: функции , , определены на , , – -мерное вещественное пространство, и отображают соответственно в [8]. Требуется найти

, . (2)

Решение данной задачи можно свести к решению задачи с одним критерием (с помощью свертки критериев). В данной работе будем рассматривать линейную свертку критериев (1). Она позволяет объединить в виде линейной комбинации все частные целевые функции в одну :

; ; . (3)

Весовые коэффициенты характеризуют относительную значимость соответствующих критериальных функций . Чем большее предпочтение мы отдаем критерию , тем больший вклад в сумму (3) он должен привносить и, следовательно, тем большее значение должно быть выбрано. Как правило, значения , , в (3) указывают эксперты. Однако при наличии существенно разнохарактерных ча­стных критериев экспертам сложно указать оконча­тельный набор коэффициентов . Поэтому предложим способ выбора , основанный на других соображениях.

Допустим вначале, что все критерии из (2) не ранжированы. Пусть заданы точки , ,..., . Вычислим значения , , , и построим линейную комбинацию

, , в которой , , предлагается выбирать (приближенно) путем решения следующей задачи квадратичного программирования:

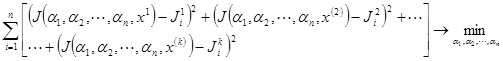; (4)

; (5)

, . (6)

Для численного решения этой задачи можно использовать различные инструментальные средства, например, офисные приложения электронных таблиц Excel.

Пусть теперь критерии, , ранжированы следующим образом:

, (7)

где , , означает, что критерий не менее предпочтителен, чем критерий . Однако степень предпочтительности по отношению к неизвестна (не указана). В этом случае (если , , ранжированы согласно (7)), очевидно, , , должны удовлетворять, кроме условий (5), (6), дополнительному условию

. (8)

Таким образом, решение многокритериальной задачи (2) можно свести, не прибегая к помощи экспертов, к решению одной из задач: (4) – (6), (3) или (4) – (6), (8), (3). В рассматриваемом случае от модели (1) с двумя критериями путем линейной свертки критериев можно перейти к модели с одним критерием:

, (9)

, . (10)

которая может быть исследована одним из описанных выше способов.

Пример 1. Для принятия решения о выдаче кредита ОАО «Ленмолоко» банком были использованы статические данные за лет [7], , ; рассматриваются стратегии – выдавать кредит, – выдавать кредит не более чем на год, – выдавать кредит не более чем на 2 года, – не выдавать кредит, тыс. руб. На основе этих данных проведены вычисления, полученные результаты представлены в табл.1.

Таблица 1. Средние ожидаемые доходы и риски стратегии .

Производя свертку в (1), получим выражение (9), для максимизации которого, согласно (4), рассчитаем весовые коэффициенты , . Они оказываются равными ; . Воспользовавшись офисным приложением электронных таблиц Excel, найдем решение (9) при ограничениях (10): при –; при – ; – . Очевидно, что является максимальным значением среднего дохода банка. Это означает, что банку рекомендуется придерживаться стратегии , то есть выдавать кредит предлагаемому предприятию на срок не более 2–х лет.

Рецензенты:

Уртенов М.Х., д.ф-м.н, профессор, заведующий кафедрой прикладной Математики ФГБОУ ВПО «Кубанский государственный университет», г. Краснодар.

Луценко Е.В., д.э.н., к.т.н., профессор кафедры компьютерных технологий и систем ФГБОУ ВПО «Кубанский государственный аграрный университет», г. Краснодар.

Бичурин Мирза Имамович, д.ф.-м.н., профессор, заведующий кафедрой ПТРА, Новгородский государственный университет, г. Великий Новгород.

Библиографическая ссылка